Fast Planner论文笔记(1)

Robust and Efficient Quadrotor Trajectory Generation for Fast Autonomous Flight

摘要——本文提出了一种鲁棒、高效的用于三维复杂环境下快速飞行的四旋翼运动规划系统。采用动态路径搜索方法，在离散控制空间中寻找安全、可行、时间最短的初始轨迹。我们通过B样条优化提高了轨迹的平滑度和净空度，该优化结合了欧几里德距离场的梯度信息和动态约束，有效地利用了B样条的凸包特性。最后，通过将最终轨迹表示为非均匀B样条，采用迭代时间调整法来保证轨迹的动态可行性和非保守性。

1 INTRODUCTION

四旋翼轨迹生成两个待解决的关键问题：
（1）给定有限时间和机载计算资源，现有方法不能高成功率地生成安全且动力学可行的轨迹。然而，轨迹生成的效率和鲁棒性是十分重要的。
（2）为保证生成动作的动力学动态可行性（kinodynamic feasibility），速度和加速度约束经常被设的很保守。因此，生成的轨迹无法适应高速飞行的应用场景。

本文采用了基于启发式搜索的kinodynamic路径搜索算法和线性二次最小时间控制，可以在离散控制空间内有效地安全、可行和时间最短的初始路径。然后利用B样条的凸包性将梯度信息和动态约束结合起来，对初始路径进行优化。最后，用非均匀B样条表示轨迹，并为此研究了导数控制点与时间分配之间的关系。并在此基础上，使用迭代时间调整方法，在避免将速度和加速度限制地过于保守的同时除去不可行的规划。

（1）提出了一种鲁棒高效的系统方法，将kinodynamic路径搜索、B样条优化和时间调整结合起来，自下而上地构成了安全性、动态可行性和进取性。
（2）基于B样条的凸包性表示优化方程，巧妙地将梯度信息和动态约束结合起来，这样可以迅速收敛，生成平滑、安全且动态可行的路径。
（3）研究了导数的控制点与非均匀B样条的时间分配之间的关系。基于该关系的时间调整方法可以保证可行且不保守的运动。
（4）仿真和实际评估。

2.1 硬约束方法：

硬约束方法的先驱是minimum-snap轨迹生成，将轨迹表示为分段多项式，通过求解二次规划(QP)问题生成轨迹。…… 非均匀B样条的使用保证了动态可行性，但可能会生成保守的动作。这些方法的一个共同缺点是轨迹的时间分配是由原始启发函数给出的，不合适的时间分配会严重降低轨迹质量。此外，只能通过迭代地增加约束和解决QP问题来得到可行解，这对于实时应用是不理想的。为了解决这些问题，Btraj提出了一种方法。硬约束方法通过凸优化来保证全局最优性。但是，忽略了自由空间内与障碍物的距离，这常常会导致轨迹过于靠近障碍物。此外，动力学约束过于保守，无法满足快速飞行的速度要求。

2.2 软约束方法：

有些方法考虑了平滑性和安全性，将轨迹生成问题化成非线性优化问题。…… 软约束方法利用梯度信息推动轨迹远离障碍物，但存在局部极小问题，在成功率和动力学可行性方面没有很强的保证。本文的优化方法也利用了梯度信息来提高轨迹的安全性。但是，与以往计算沿轨迹线积分的方法不同，本方法基于B样条的凸包性，将公式设计得更加简单。这大大提高了计算效率和收敛速度。

3 KINODYNAMIC PATH SEARCHING

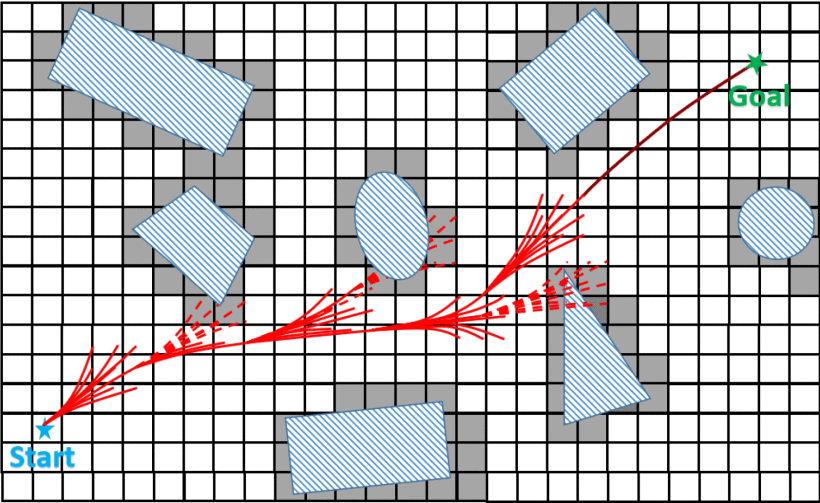
本前端kinodynamic路径搜索算法源自hybrid-state A* 。它会寻找安全且kinodynamic可行的路径，并最小化在voxel grid map中的持续时间和控制成本。如Alg.1和Fig.2所示，搜索环路和标准A* 类似，其中\(\mathcal{P}\)和\(\mathcal{C}\)分别代表open表和closed表。图边（ graph edge）采用四旋翼动力学的运动基元（primitive），而不是直线。用结构体 Node记录primitive、primitive结束时的体素和\(g_c\)、\(f_c\)成本（Sect 3.2）。Expand()迭代地扩大体素栅格地图，那些在同一个体素结束的（除了拥有最小\(f_c\)的）会被删除（Prune()）。然后CheckFeasible()会检查留下的primitives的安全性和动态可行性。这个过程一直持续到任意一个primitive到达目标或者AnalyticExpand() 成功。

3.1 Primitives Generation

首先，讨论Expand()中使用的motion primitives生成。四旋翼系统的微分平坦使得我们可以用三个独立的1-D时间参数的多项式函数来表示轨迹[1]。

\[\mathbf{p}(t):=[p_x(t),p_y(t),p_z(t)]^T , p_\mu (t) = \sum_{k=0}^K a_kt^k \tag{1}\]

其中，\(\mu \in \{x,y,z\}\)。从四旋翼系统的角度看，它符合线性时不变（LTI）系统。令 \(\mathbf{x}(t) := [\mathbf{p}(t)^T, \dot{\mathbf{p}}(t)^T, \ldots, \mathbf{p}^{(n-1)}(t)^T]^T \in \mathcal{X} \subset \mathbb{R}^{3n}\) 为状态向量。令 \(\mathbf{u}(t) := \mathbf{p}^{(n)}(t) \in \mathcal{U}:=[-u_{\max},u_{\max}] \subset \mathbb{R}^3\) s 为控制输入。状态空间模型可以定义为：

\[\begin{equation}\begin{split} & \dot{\mathbf{x}} = \mathbf{Ax+Bu} \\ & \mathbf{A} = \begin{bmatrix} 0 & \mathbf{I_3} & 0 & \cdots & 0 \\ 0 & 0 & \mathbf{I_3} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots \vdots \\ 0 & \cdots & \cdots & 0 & \mathbf{I_3} \\ 0 & \cdots & \cdots & 0 & 0 \\ \end{bmatrix}, \mathbf{B} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ \mathbf{I_3} \\ \end{bmatrix} \end{split}\end{equation} \tag{2}\]

状态方程的完全解可以表示为：

\[\mathbf{x}(t) = e^{\mathbf{A}t} \mathbf{x}(0) + \int_0^t{e^{\mathbf{A}(t-\tau)} \mathbf{Bu}(\tau) d\tau} \tag{3}\]

给出了四旋翼系统在初始状态为\(\mathbf{x}(0)\)控制输入为\(u(t)\)的情况下的轨迹。

在Expand()中，给定四旋翼的当前状态，在持续时间\(\tau\)内应用一系列离散的控制输入\(\mathcal{U}_D \subset \mathcal{U}\)。在实际操作时，选定\(n=2\)，对应二次积分。每个坐标轴\([-u_{\max},u_{\max}]\)被均匀地离散化为 \(\{-u_{\max},-\frac{r-1}{r}u_{\max},\ldots,\frac{r-1}{r}u_{\max},u_{\max} \}\) ，会带来\((2r+1)^3\)个primitives。

3.2 Actual Cost and Heuristic Cost

由于我们希望找到一条时间和控制代价最优的轨迹，所以把轨迹的代价函数定义为

\[\mathcal{J}(T) = \int_0^T{\|\mathbf{u}(t)\|^2 dt + \rho T} \tag{4}\]

在此定义下，EdgeCost()按\(e_c=(\|\mathbf{u}_d\|^2 + \rho) \tau\)计算离散输入\(\mathbf{u}(t) = \mathbf{u}_d\)，持续时间\(\tau\)时生成的运动primitives的代价。

沿用A*中的术语，用\(g_c\)表示从开始状态\(\mathbf{x}(s)\)到当前状态\(\mathbf{x}(c)\)的最优路径的实际代价。令这条最优路径由\(J\)个primitives构成，\(g_c\)可以由\(g_c = \sum_{j=1}^J{(\|\mathbf{u}_{dj}\|^2 + \rho) \tau}\)计算得到。

一个可行且含有效信息的启发函数对于加速A*的搜索十分重要。因此，本文利用Pontryagins minimum principle来计算可以最小化从\(\mathbf{x}(c)\)到目标状态\(\mathbf{x}(g)\)的\(\mathcal{J}(T)\)的闭式轨迹：

\[\begin{equation}\begin{split} & p_{\mu}^*(t) = \frac{1}{6}\alpha_{\mu}t^3 + \frac{1}{2}\beta_{\mu}t^2 + v_{\mu c} + p_{\mu c} \\ & \begin{bmatrix} \alpha_{\mu} \\ \beta_{\mu} \end{bmatrix} = \frac{1}{T} \begin{bmatrix} -12 & 6T \\ 6T & -2T^2 \\ \end{bmatrix} \begin{bmatrix} p_{\mu g} - p_{\mu c} - v_{\mu c}T \\ v_{\mu g} - v_{\mu c} \end{bmatrix} \\ & \mathcal{J}^*(T) = \sum_{\mu \in \{x,y,z \}} {\left( \frac{1}{3}\alpha_{\mu}^2 T^3 + \alpha_{\mu} \beta_{\mu} T^2 + \beta_{\mu}^2 T \right)} \\ \end{split}\end{equation} \tag{5}\]

其中，\(p_{\mu c},v_{\mu c},p_{\mu g},v_{\mu g}\)是当前和目标处的位置和速度。\(\mathcal{J}^*(T)\)是式(4)定义的成本函数。为了求出最小化成本的最优时间\(T\)，把\(\alpha_{\mu},\beta_{\mu}\)代入\(\mathcal{J}^*(T)\)中，并求出\(\frac{\partial \mathcal{J}^*(T)}{\partial T} =0\)的根。这个根\(T_h\)会选出最小成本\(\min \mathcal{J}^*\)和可行轨迹。用\(\mathcal{J}^*(T_h)\)表示启发函数\(h_c\)。最后，\(f_c\)被定义为\(f_c = g_c + h_c = g_c + \mathcal{J}^*(T_h)\)。

3.3 Analytic Expansion

由于控制输入是离散的，所以很难找到准确地结束在目标状态的primitive。为了补偿这点以及加速搜索，本文引入了一种分析扩张（Analytic Expansion）方案。当一个节点从open表出栈的时候，就会采用和3.2节中相同的方法来计算从\(\mathbf{x}_c\)到\(\mathbf{x}_g\)的轨迹。如果它通过了安全性和动态可行性检查，那么搜索提前结束。这个策略在提高效率方面很有效，尤其是在稀疏环境中，因为它的成功率更高并且搜索结束地更早。

3.4 Optimality and Completeness

理论上讲，无法保证路径搜索的最优性和完整性，但是实际的表现是令人满意的。对于最优性而言，第3.1节中的评价表明牺牲最优性是可以接受的和可调整的。此外，给出的初始路径在最优路径的附近，第4章的优化会找到最优解。对于完整性而言，第3.1节中的评价表明该方法在大多数情况下是可以找到可行解的。另外，本文的方法也可以拓展支持变时间的（variable-duration）的primitives，文献[15]中的变分辨率voxel grid可以有更强的完整性保证。