Sequence as Input
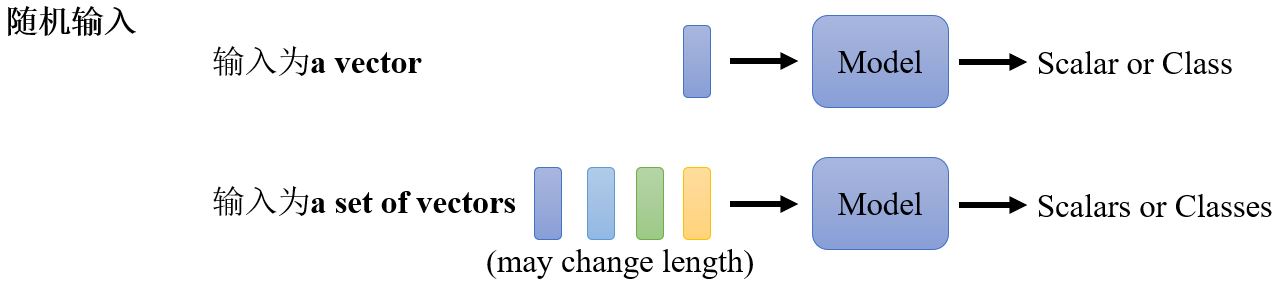
目前为止,我们的网络的输入都是一个vector,输出可能是一个数值或者一个类别。那如果我们的输入是一排向量呢?输入的数量(即序列的长度)会改变呢?我们又该如何处理呢?
Vector set as input
什么情况下输入是一个长度可变的序列呢?
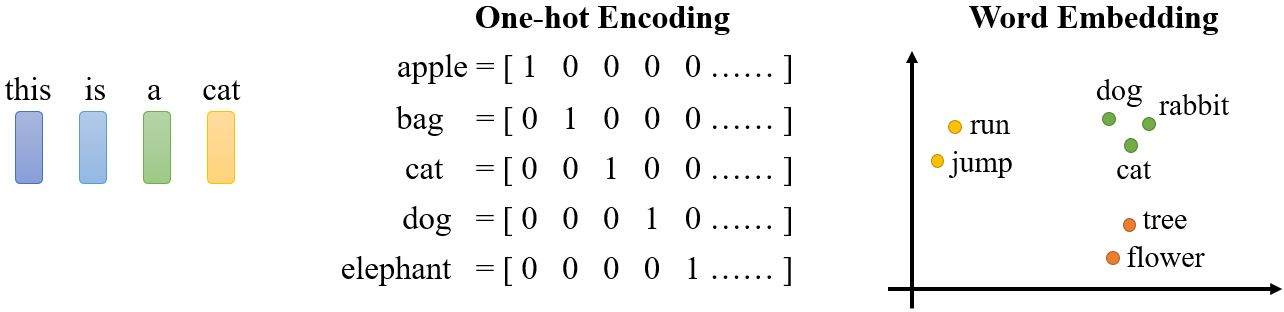
输入是一个句子,把句子中的每个词汇描述成一个向量,那么model的输入就是大小会变的vector set。如果采用one-hot encoding对词汇进行编码,那么每个词汇就对应一个独热向量。另一种方法是word embedding,每个词对应一个包含语义信息的向量。
To learn more: https://youtu.be/X7PH3NuYW0Q (in Mandarin)

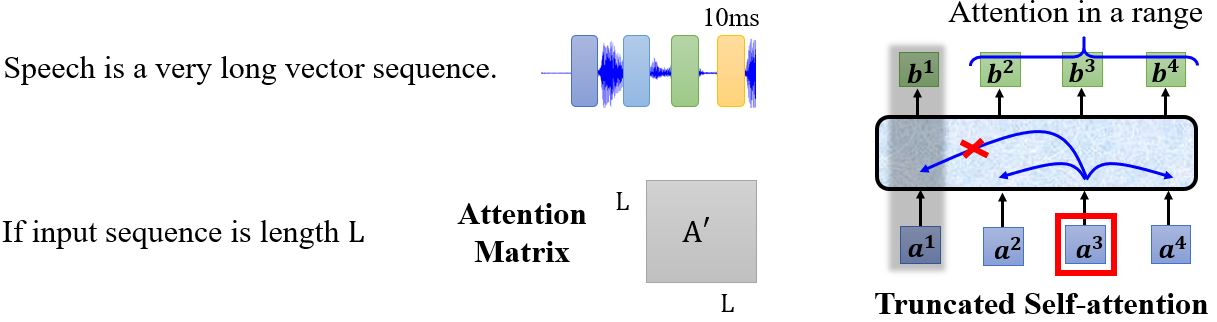
一段声音信号也是一排向量,一个window内的信号可以描述成一个向量(有很多种描述方法),称为frame,窗口每次向右移10ms。
Graph也是一组向量 (consider each node as a vector)。
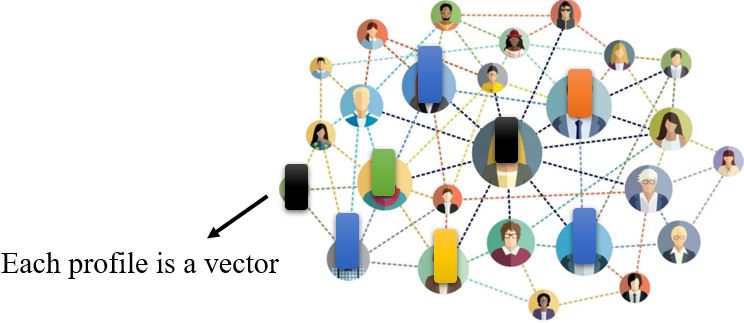
social network就是一个graph,其中每个node就是一个人,节点与节点间的edge就是两个人之间的关系,每个节点可以看作一个向量,其中包含了这个人的各种相关信息,所以整个graph可以看作是一堆向量组成的。
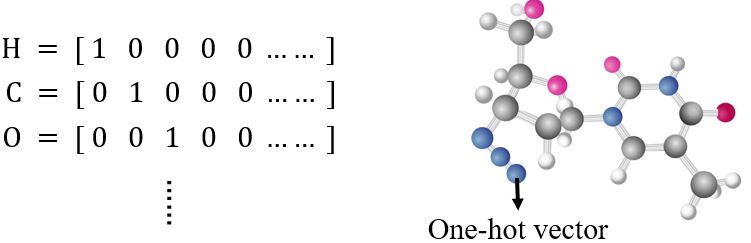
一个分子也是一个graph,每个原子可以用一个one-hot vector表示,一个分子就是一堆向量。
What is the output?
1. 每个向量都有一个对应的label Sequence Labeling(本节主要关注的情况)

Example applications
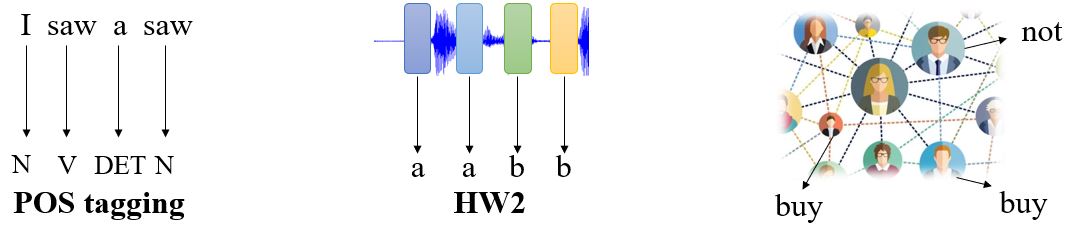
2. 每个序列对应一个label

Example applications

3. 模型自己决定label的数量 seq2seq

4.1 Self-attention
Sequence labeling
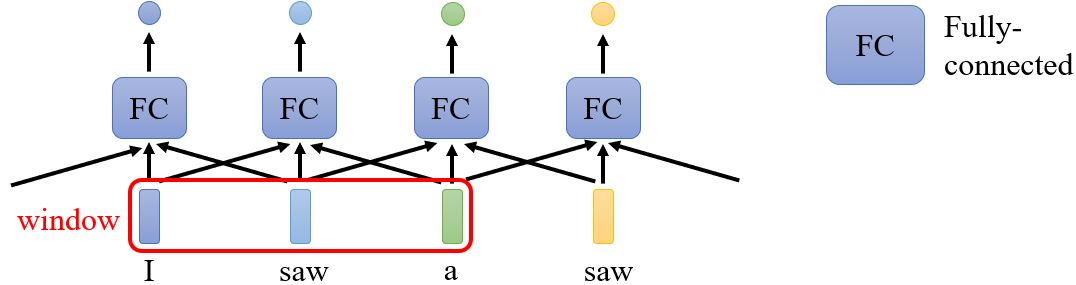
如果用全连接结构来解决这个问题,可以考虑上下文吗?FC可以考虑附近的内容。如何让考虑整个序列呢?用一个覆盖整个序列的窗口吗?
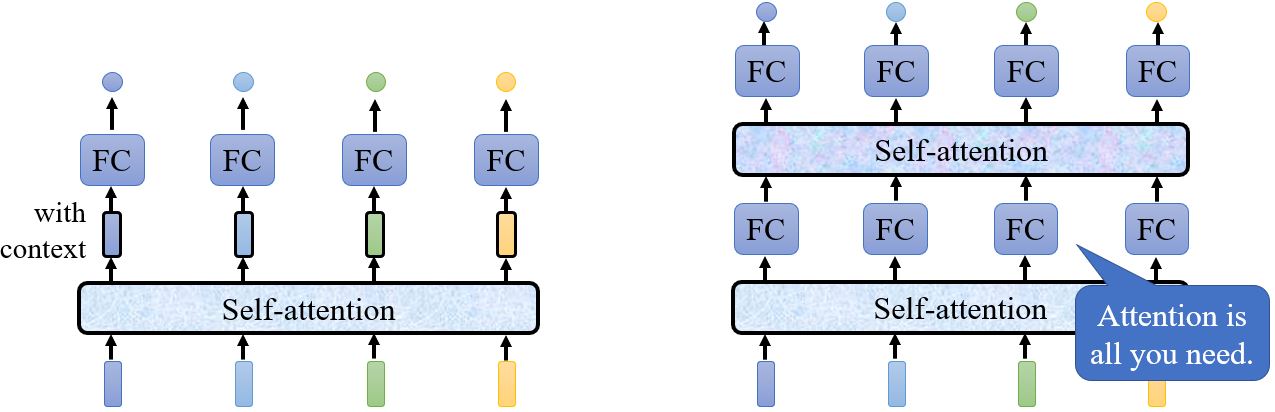
Self-attention层会吃一整个序列的咨询,然后输出与输入数量相同的vector,自注意力层可以和全连接层交替使用。
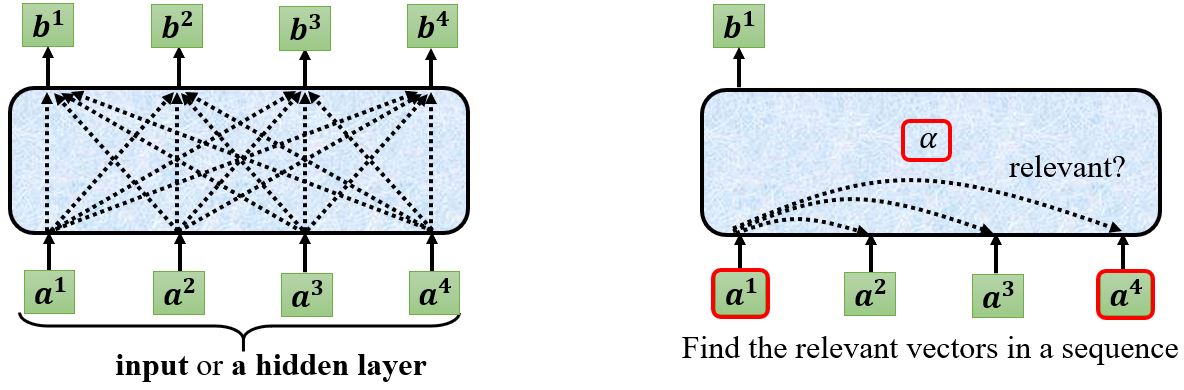
首先根据\(\mathbf{a^1}\)找出序列中与\(\mathbf{a^1}\)相关的其它向量,每个向量与\(\mathbf{a^1}\)的关联程度可以用数值\(\alpha\)来表示。那么自注意力机制中的module怎么决定两个向量之间的关联性呢?
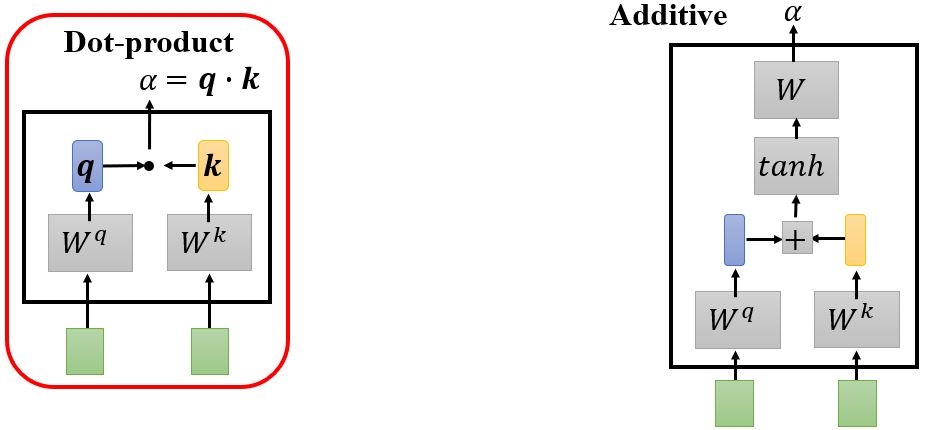
计算attention有很多种方法,e.g. dot-product、additive… 比较常用的是dot-product(transformer中采用的方法),下面以dot-product为例讲解。
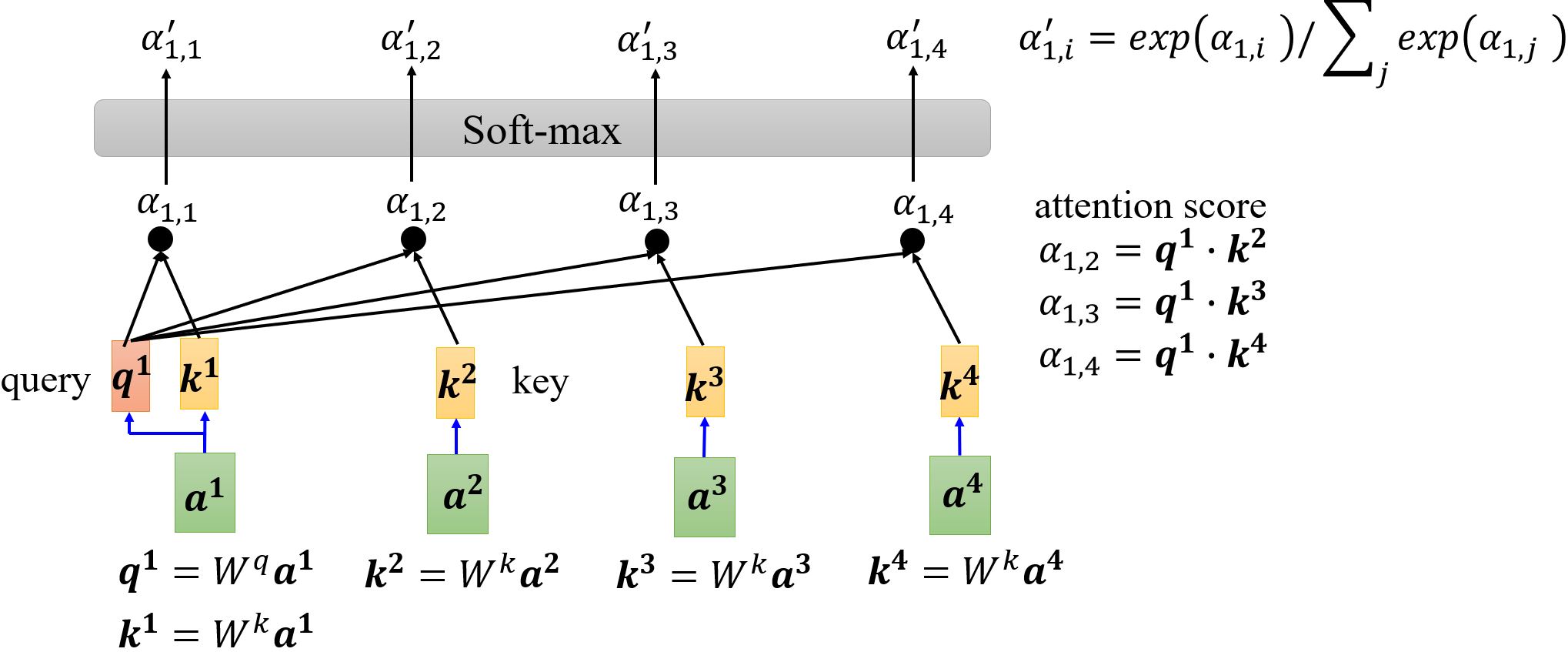
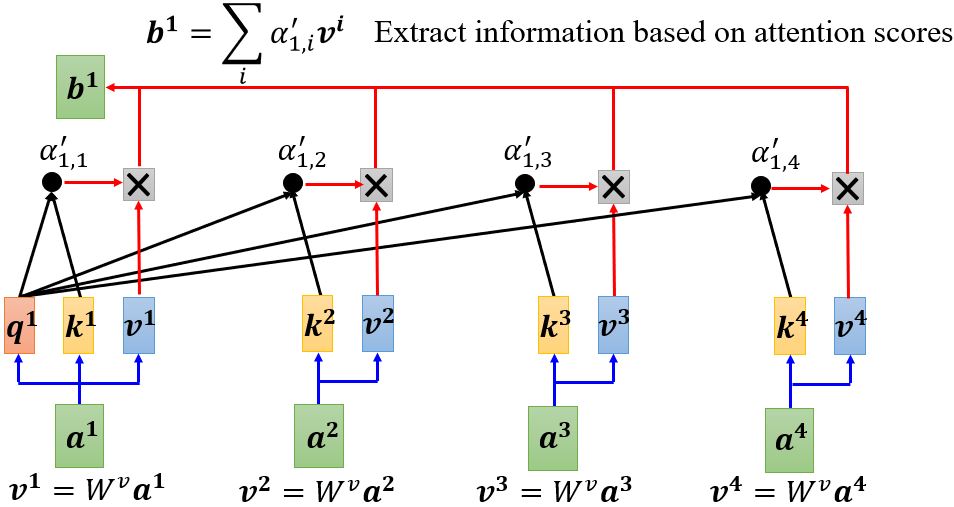
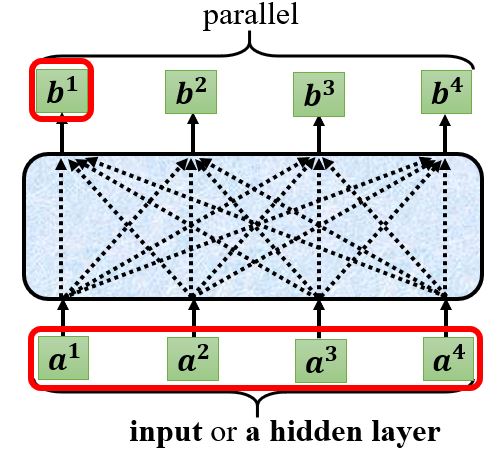
这样我们就得到了\(\mathbf{b^1}\),下面开始计算\(\mathbf{b^2}\)。需要注意的是,这里\(\mathbf{b^1}, \ldots, \mathbf{b^4}\)并不需要依次计算,而是同时计算出来的。
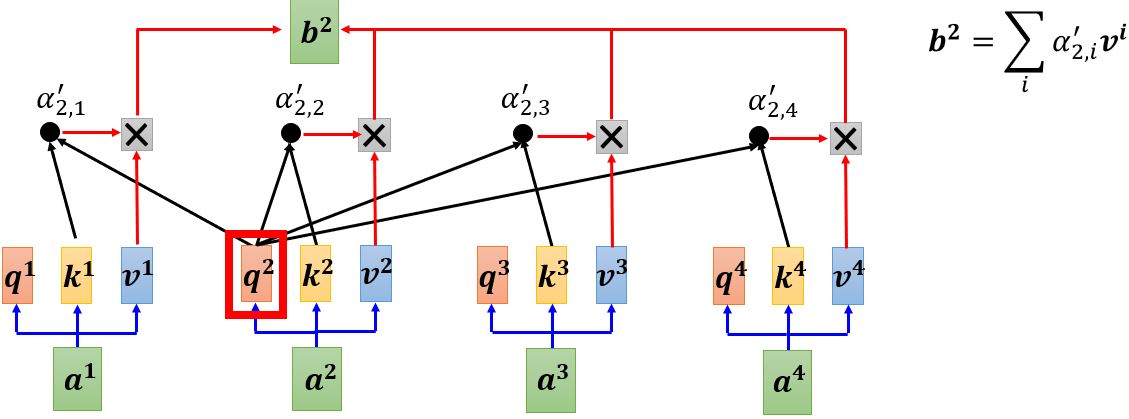
下面我们再从矩阵的角度重新解释一下self-attention是如何运作的。
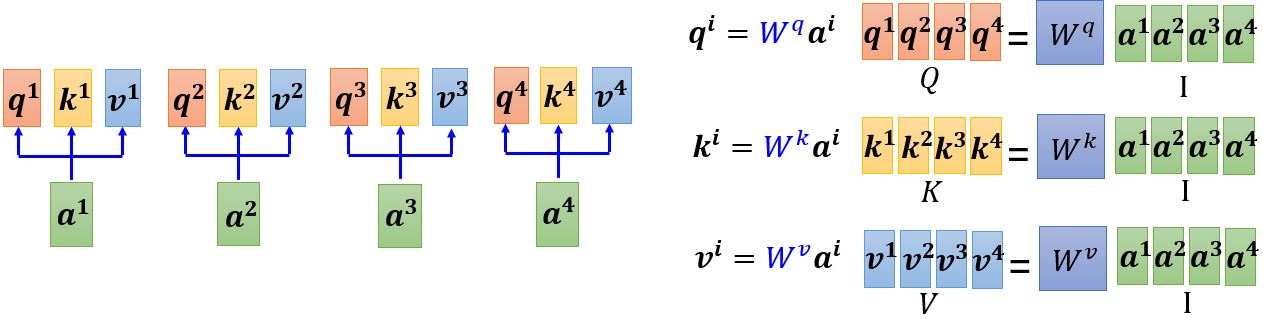
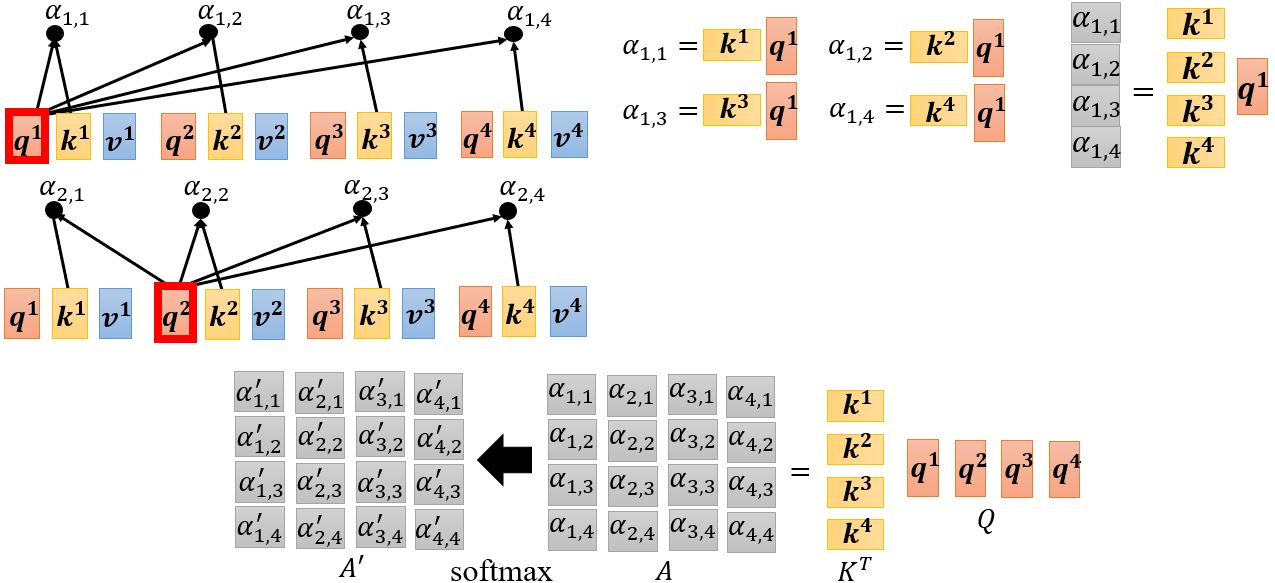

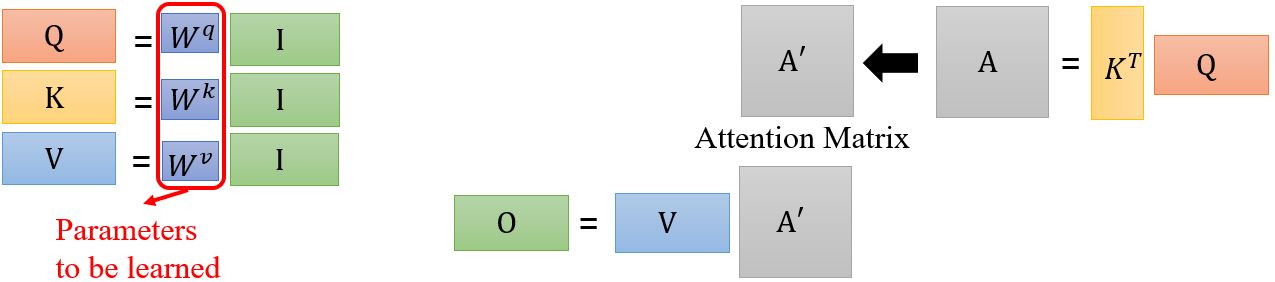
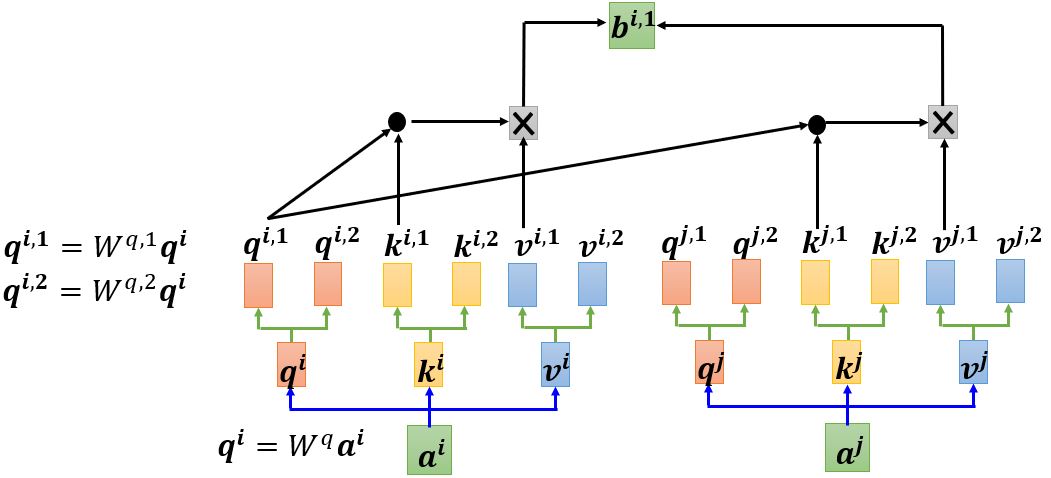
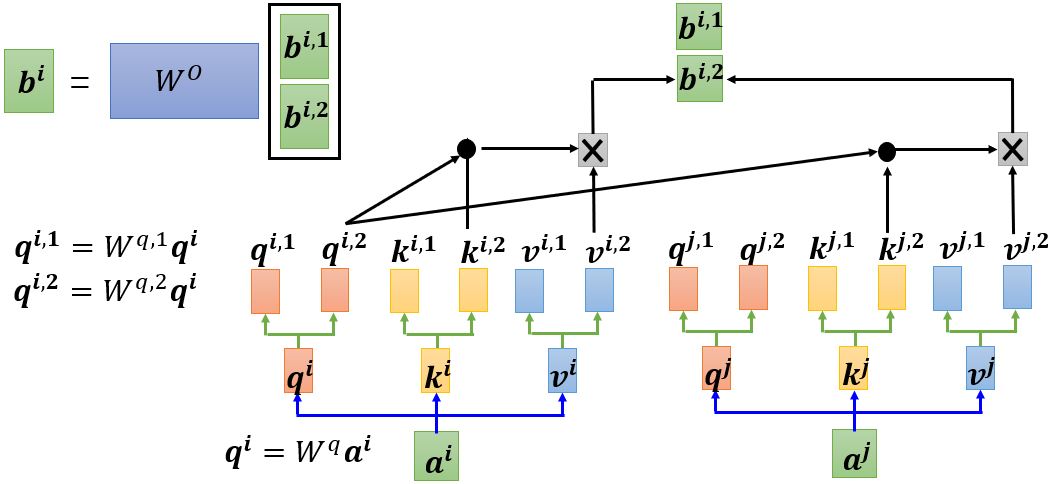
4.2 Multi-head Self-attention
多头注意力机制现在也很常用,可以判断different types of relevance。head的个数也是一个hyperparameter,下面以2 heads为例。
4.3 Positional Encoding
对于self-attention层而言,每个数据出现在序列的哪个位置没有区别。所以我们需要做positional encoding,每个位置都有一个唯一的positional vector \(e^i\)。
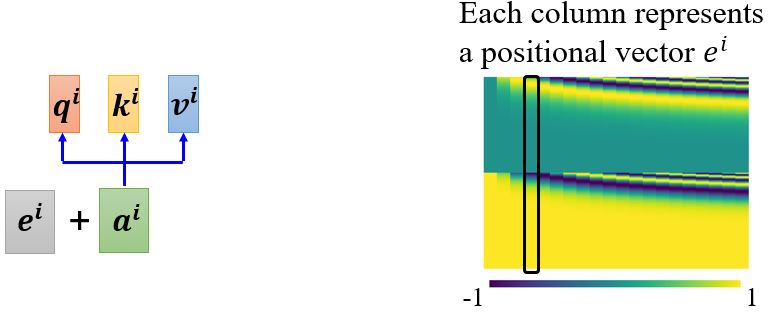
不同的编码方式:
- hand-crafted(这可能会带来一些问题,比如序列的长度比编码长度长)
- learned from data
Positional encoding仍是一个尚待研究的问题,比如2020年发表在arxiv上的一篇论文中的工作如下:
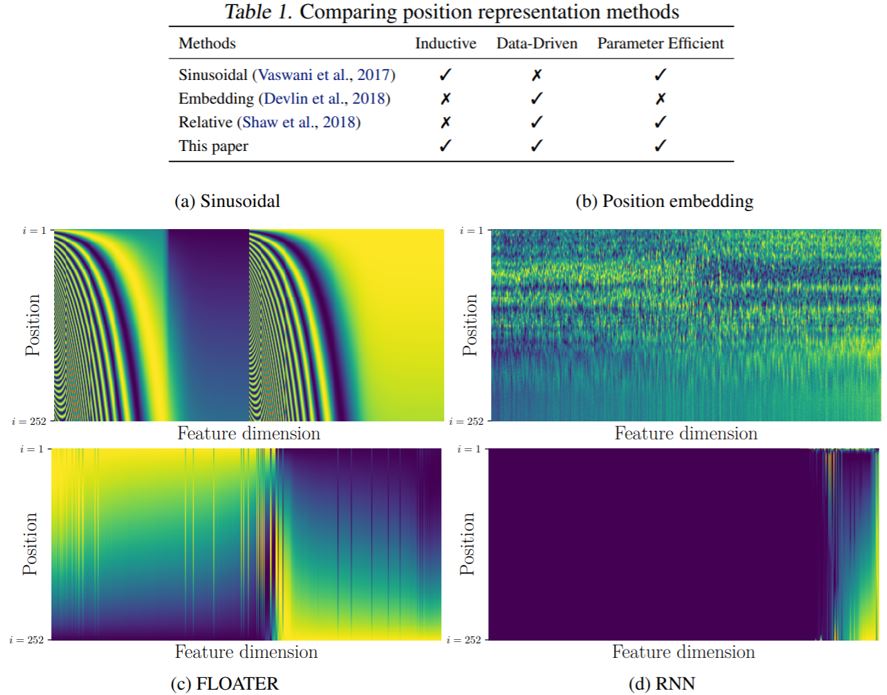
4.4 Many Applications
Self-attention应用广泛,如Transformer、BERT……广泛运用在Natural Langue Processing (NLP)中!
4.4.1 Self-attention for speech
一段语音信号是一个非常长的序列,如果输入序列长度为\(L\),那么attention matrix \(\mathbf{A'}\)会是一个\(L \times L\)的非常大的矩阵。在语音辨识中有一种方法,Truncated Self-attention。因为Self-attention没有必要关注整个句子,可以只考虑句子的一部分,这样可以加快计算。
4.4.2 Self-attention for image

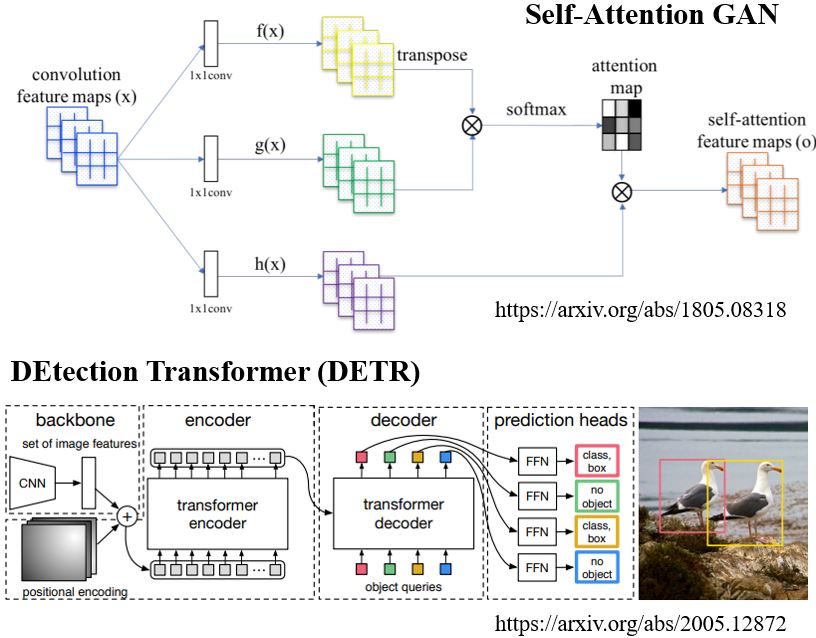
Self-attention v.s. CNN

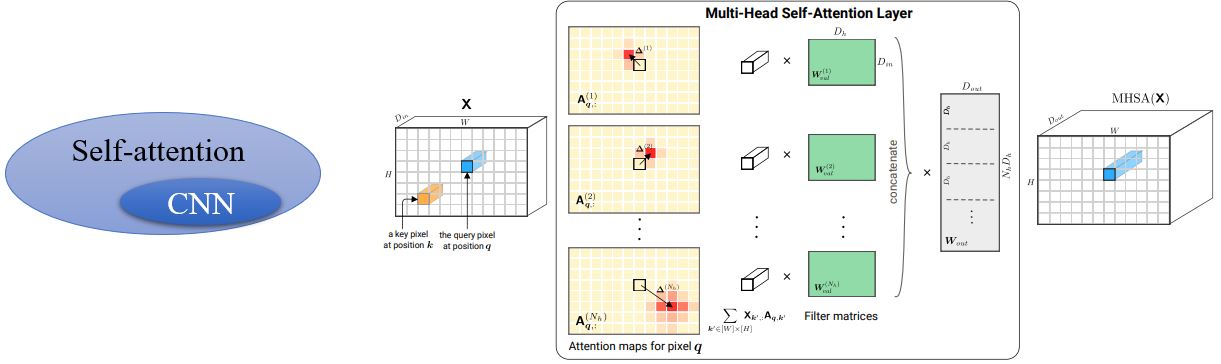
On the Relationship between Self-Attention and Convolutional Layers一文详细证明了CNN是Self-attention的一个特例,只要Self-attention参数合适就可以做到和CNN一样的事情。
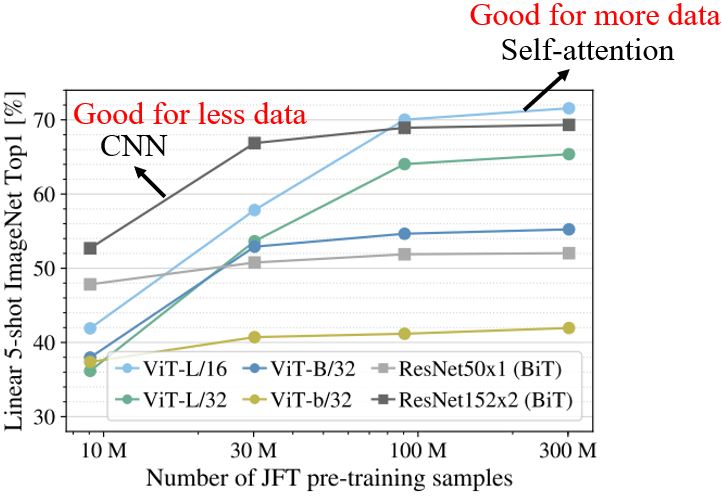
CNN是Self-attention的一个subset,那么Self-attention会比较flexible,会比较需要更多的data,如果data不够可能会overfitting。
Self-attention v.s. RNN
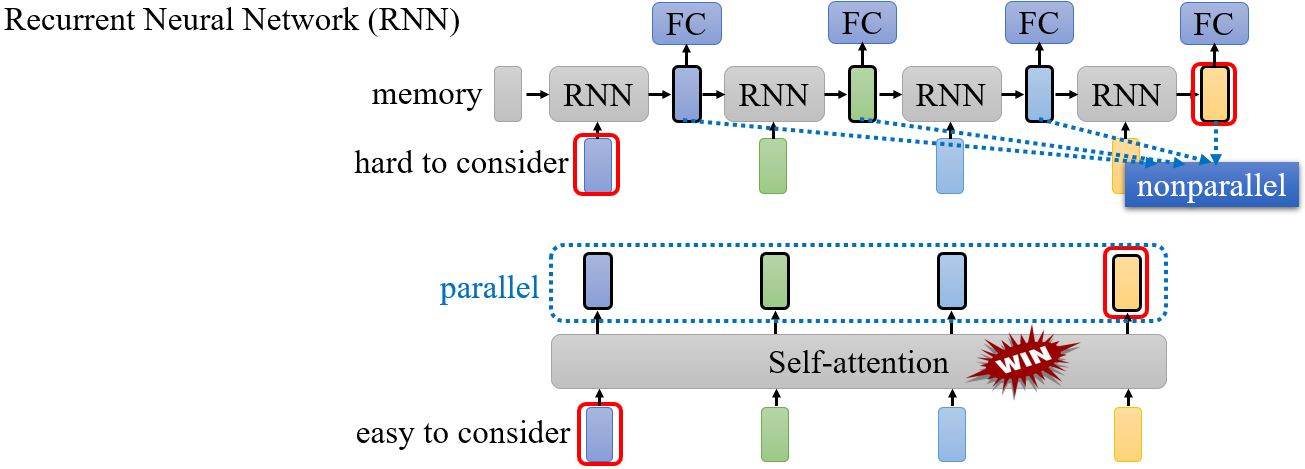
两者对比:Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
To learn more:ML Lecture 21-1: Recurrent Neural Network (Part I) Youtube bilibili
4.4.3 Self-attention for graph
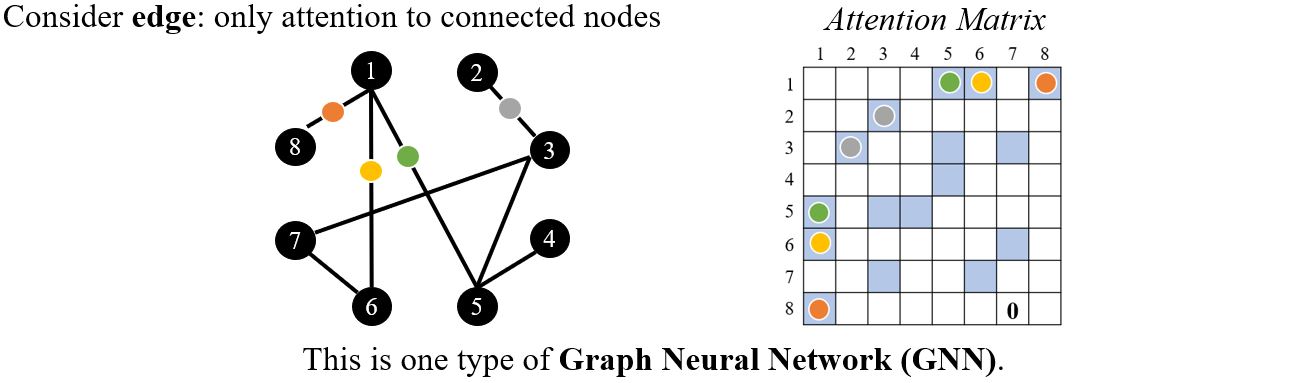
只考虑edge:只对相连的节点计算attention。(将自注意力机制用在Graph Neural Network (GNN)上,是某一种类型的GNN。)
To learn more:[TA 补充课] Graph Neural Network (1/2) Youtube bilibili
To learn more
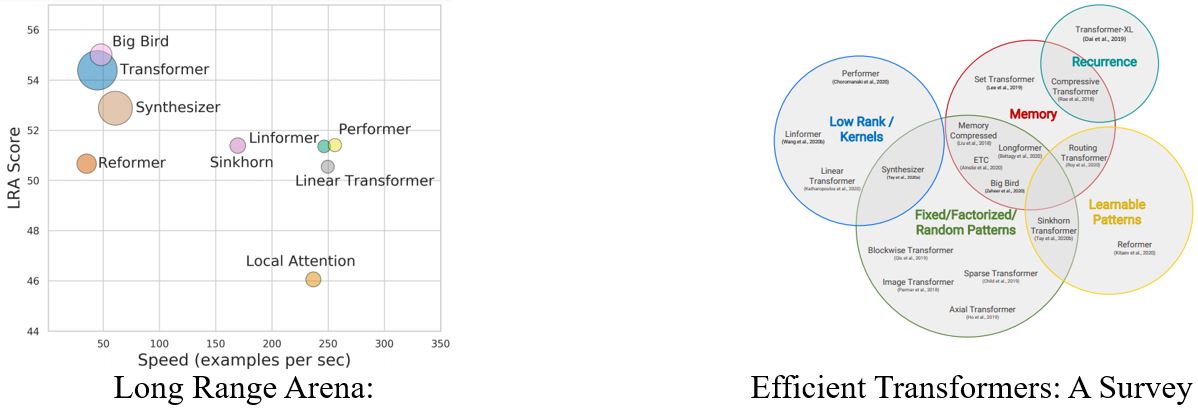
Self-attention的变形非常多,Long Range Arena: A Benchmark for Efficient Transformers中比较了不同的变形。Self-attention的运算量非常大,所以如何减小运算量是未来的一个研究方向。 关于Self-attention的变形也可以参考Efficient Transformers: A Survey。
