Configuration Space
要为机器人作运动规划,我们必须要给出机器人上每个点的位置说明,因为我们需要确保机器人上的任何点都不会与障碍物相撞。这就提出了一些基本的问题:需要多少信息才能完全指定机器人上每个点的位置?该如何表示这些信息?这些表示的数学性质是什么?在规划机器人的路径时,如何考虑机器人世界中的障碍?
在本章中,我们开始解决这些问题。首先,我们讨论了机器人构型的确切含义,并介绍了构型空间的概念,这是机器人运动规划中最重要的概念之一。然后我们简要讨论机器人环境中的障碍物是如何限制可行路径的集合的。然后,我们开始对构型空间的性质进行更严格的研究,包括它的维数,它有时如何用可微流形表示,以及流形如何用嵌入和参数化表示。最后我们将讨论构型的不同表示之间的映射以及这些映射的雅可比矩阵,即用不同的表示方法把速度联系起来。
3.1 Specifying a Robot's Configuration
机器人系统的configuration是系统每一点位置的complete specification。机器人的configuration space(或C-space)是系统所有可能构型构成的空间。因此,构型只是抽象的构型空间中的一个点。本书中用\(\color{green}{q}\)表示构型,用\(\color{green}{\mathcal{Q}}\)表示构型空间。一个机器人系统的自由度的数量就是构型空间的维度,或者说是用于指定构型所需的最少的参数的个数。
以平面内可以任一平移(无需旋转)的圆形移动机器人为例,一个比较简单的表示机器人构型的方法就是确定其中心关于某个固定坐标系所在的位置\((x, y)\)。如果知道机器人的半径\(r\),就可以很容易地从构型\(q = (x, y)\)确定机器人占据的点集,我们用\(R(q)\)来表示这个点集。当我们把构型定义为\(q = (x, y)\)时,我们有\(R(x, y) = \{ (x', y') \mid (x - x')^2 + (y- y')^2 \le r^2 \}\)。其中,参数\(x\)和\(y\)足以完全确定圆形机器人的构型。因此,一旦确定了平面内的坐标系,就可以用\(\mathbb{R}^2\)来描述圆形移动机器人的构型。
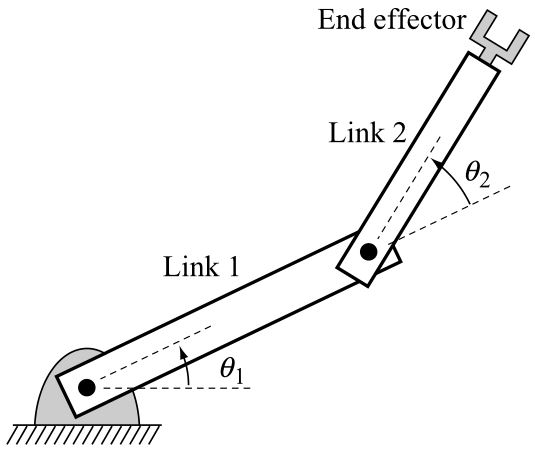
机器人在二维或三维欧几里得环境空间(分别表示为\(\mathbb{R}^2\)和\(\mathbb{R}^3\))中移动时,有时我们会把这个环境空间称为workspace。其他时候,我们对"workspace"会有一个更具体的含义。比如,对于机械臂,我们一般把手部或末端执行器(end effector)上的点到达的环境空间点的集合称为工作空间(图3.3)。对于上述平移的移动机器人,工作空间和构型空间都是二维欧几里得空间,但要注意它们其实是不同的空间。下面我们考虑稍微复杂一点的机器人时,这点会体现得更清楚。
## 3.6 Parameterizations of SO(3) 从前面的内容可以看出,旋转矩阵$$ R \in SO(3) $$的9个元素$$ R_{ij} $$受6个条件约束,剩下3个旋转自由度。因此,我们希望可以用3个变量来对$$ SO(3) $$作局部参数化。欧拉角是一种常见的参数化,但是我们无法用欧拉角来对$$ SO(3) $$作全局参数化。 ## 3.7 Example Configuration Spaces 设计运动规划器的时候,理解机器人构型空间的基础结构通常是十分重要的。 * $$ S^1 \times S^1 \times \cdots \times S^1 (n \text{times}) = T^n $$,n维圆环面 * $$ S^1 \times S^1 \times \cdots \times S^1 (n \text{times}) \neq S^n $$,$$ \mathbb{R}^{n+1} $$中的n维球体 * $$ S^1 \times S^1 \times S^1 \neq SO(3) $$ * $$ SE(2) \neq \mathbb{R}^3 $$ * $$ SE(3) \neq \mathbb{R}^6 $$ 有的时候流形是否是紧的很重要。流形$$ S^n $$,$$ T^n $$和$$ SO(n) $$都是紧的,它们互相直接相乘也是紧的。而流形$$ \mathbb{R}^n $$和$$ SE(n) $$不是紧的,因此$$ \mathbb{R}^n \times \mathcal{M} $$也不是紧的。 以上构型空间有一个重要的相同点:当它们被装进atlas时,都是可微流形。其中, * $$ \mathbb{R}^1 $$和$$ SO(2) $$是一维流形 * $$ \mathbb{R}^2 $$,$$ S^2 $$和$$ T^2 $$是二维流形 * $$ \mathbb{R}^3 $$,$$ SE(2) $$和$$ SO(3) $$是三维流形 * $$ \mathbb{R}^6 $$,$$ T^6 $$和$$ SE(3) $$是六维流形 ## 3.8 Transforming Configuration and Velocity Representations e.g. $$q$$表示机器人手臂的连接角度,$$x$$表示终端传感器在周围空间内作为刚体的构形。规划操作的时候,用$$x$$表示更方便,但是控制机器人手臂的时候用$$q$$变量更方便,所以需要在两种表达方式之间切换。然而$$\mathcal{Q}$$和$$\mathcal{M}$$往往不是同胚的,甚至两个空间的纬度都不相等。 定义foward kinematics map $$\color{green}{\Phi : \mathcal{Q}} \rightarrow \mathcal{M}$$,以及inverse kinematics map $$\color{green}{\Phi^{-1} : \mathcal{M}} \rightarrow \mathcal{Q}$$。随着机器人系统移动,$$ \dot{x} = \frac{dx}{dt} $$和$$ \dot{q} = \frac{dq}{dt} $$的关系为 $$ \dot{x} = \frac{\partial \Phi}{\partial q} = J(q) \dot{q} $$ 其中,$$ J $$是映射$$ \Phi $$的Jacobian,即微分$$ D \Phi $$(见附录C)。Jacobian也可以用于把一组坐标表示的力转化到另一组(见第4章4.7和第10章)。 ```note 关于构型空间的笔记目前还不全,但是后面我应该还会再反复读这一章以及附录里关于泛函分析的一些内容,这章里有很多思想很妙,解释了一些现有的规划方法为什么是可以这样做的。但是,作为运动规划的基础,这方面的内容很少被论文提及,这也是我第一次接触configuration space的概念。所以说还是得看一些教科书,对问题的理解才能更系统。 ```
