Model-free prediction & control

请先阅读书本的Chapter 5和Chapter 6


  • Model-free prediction: Estimate value function of an unknown MDP
  • Model-free control: Optimize value function of an unknown MDP

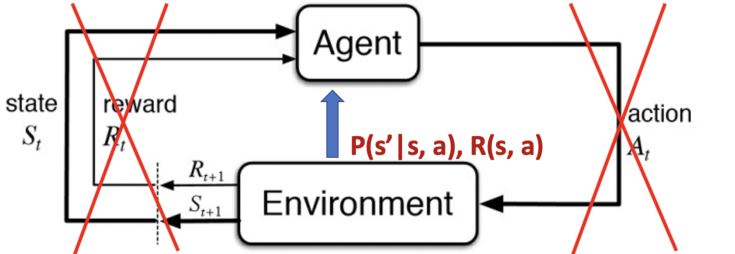
  Policy iteration和value iteration都是假设可以直接接触环境的动态过程和奖励的。然而在很多实际问题中，MDP模型可能是未知的或者过大而无法利用。

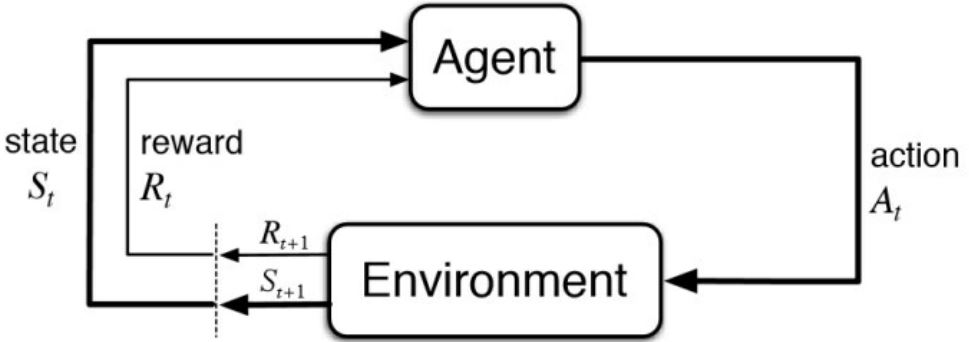
Model-free RL: learning by iteration

  • 无模型的RL可以在与环境交互的过程中解决问题
  • 不再能够直接访问已知的转移动态过程和奖励函数
  • trajectory/episodes是在agent与环境交互的过程中收集的
  • 每个trajectory/episode包含\(\{S_1, A_1, R_1, S_2, A_2, R_2, \ldots, S_T, A_T, R_T\}\)
补充

强化学习中”episode（事件）”指的是agent在环境里面根据某个策略从开始到结束这一过程，”trajectory”是一段状态动作序列。

Model-free prediction: policy evaluation without the access to the model

在无法接触MDP模型时，估计某个策略下的期望return

  • Monte Carlo policy iteration
  • Temporal Difference (TD) learning

3.1 Monte-Carlo Methods

  • Return：\(G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots\) 在策略\(\pi\)下
  • \(v^{\pi}(s) = \mathbb{E}_{\tau \sim \pi} [G_t \vert S_t = s]\)，按策略\(\pi\)生成的trajectory\(\tau\)的期望
  • MC simulation：对很多trajectory进行简单采样，计算所有轨迹的实际return，然后取平均
  • MC policy iteration使用经验平均return替代期望return
  • MC不需要MDP的动态过程/奖励，没有bootstrapping（在之前估计的基础上估计），也无需假设状态是马尔可夫的
  • 只能应用于由一系列独立事件组成的MDPs（每个episode都会终止）

  假设经验被划分为episodes，并且无论选择什么动作，所有episodes最终都会结束。只有在一个episodes完成时，价值估计和策略才会改变。因此，Monte-Carlo方法可以在"episode-by-episode"意义上是增量的，而不是在step-by-step（在线）意义上。这里的"Monte-Carlo"特指基于averaging complete return的方法。

3.1.1 MC policy iteration

  Monte-Carlo预测法可以在episode-by-episode的基础上进行增量实现。

评估状态\(v(s)\)：

  1. 在一个随机事件中访问状态\(s\)的每个时间步长\(t\)
  2. 增量计数 \(N(s) \leftarrow N(s) + 1\)
  3. 增量总return \(S(s) \leftarrow S(s) + G_t\)
  4. 值的评估根据平均return \(v(s) = S(s) / N(s)\)

根据大数定律，当\(N(s) \rightarrow \infty\)时，\(v(s) \rightarrow v^{\pi}(s)\)。

Incremental mean：来自样本\(x_1, x_2, \ldots\)的平均值

\[\begin{aligned} \mu_t & = \frac{1}{t} \sum_{j = 1}^t x_j \\ & = \frac{1}{t} \left(x_t + \sum_{j = 1}^{t-1} x_j\right) \\ & = \frac{1}{t} (x_t + (t - 1) \mu_{t - 1}) \\ & = \mu_{t - 1} + \frac{1}{t} (x_t - \mu_{t - 1}) \end{aligned}\]

Incremental MC Updates：

  1. 收集一次episode \((S_1, A_1, R_1, \ldots, S_t)\)
  2. 对于每个有\(G_t\)（计算所得的return）的状态\(S_t\)
     \(N(S_t) \leftarrow N(S_t) + 1\)
     \(v(S_t) \leftarrow v(S_t) + \frac{1}{N(S_t)} (G_t - v(S_t))\)
  3. 或者使用一个更新的均值（旧事件的影响会逐渐减小），适合解决非静态问题（\(\alpha\)可以理解为学习率）
     \(v(S_t) \leftarrow v(S_t) + \alpha (G_t - v(S_t))\)

3.1.2 DP vs. MC 策略评估

  动态规划（DP）通过价值估计\(v_{i-1}\)引导其余的期望回报的方法计算\(v_i\)。根据Bellman expectation backup迭代：

\[v_i(s) = \sum_{a \in A} \pi(a \vert s) \bigg[R(s,a) + \gamma \sum_{s' \in S} P(s' \vert s,a) v_{i-1}(s')\bigg]\]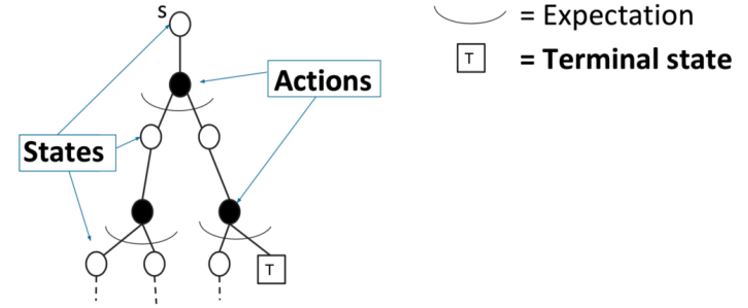

  MC用一次采样episode来更新经验平均return

\[v(S_t) \leftarrow v(S_t) + \alpha (G_{i,t} - v(S_t))\]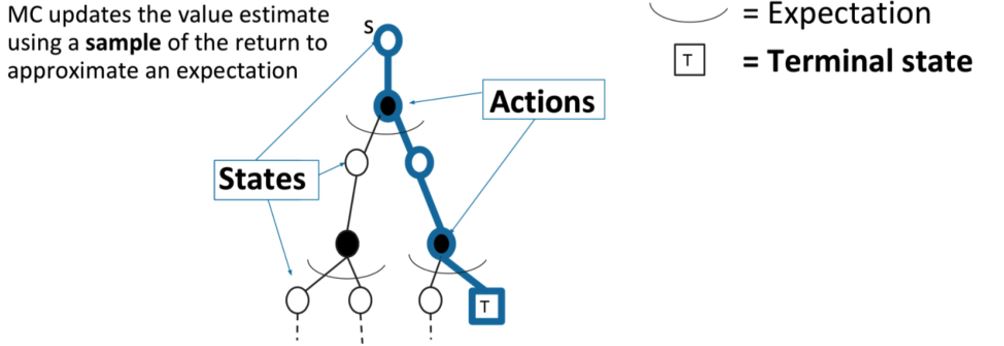

MC与DP的区别：

  1. MC根据样本经验进行操作，因此可以在没有模型的情况下直接学习。
  2. MC不会在其他价值估计的基础上更新其价值估计。
    （这两个不同点并没有紧密联系，可以分开。）

MC相较于DP的优势：

  1. MC可以用于环境未知的情况。
  2. 即使是环境动态特性完全已知的情况下，使用采样episode仍有很大的优势，e.g. 转移概率难以计算的情况。
  3. 估计某个单一的状态的值与全部状态无关。所以可从感兴趣的状态开始采样，然后再取return的平均。

3.2 Temporal-Difference Learning

  • TD法是直接从episodes的经验学习
  • TD是无模型的：MDP的转移特性/奖励
  • TD从不完整的episodes中学习，通过bootstrapping的方式。

3.2.1 one-step TD

  • 目标：根据策略\(\pi\)下的经验在轨学习\(v(\pi)\)
  • 最简的TD算法：TD(0)
      向估计return \(R_{t+1} + \gamma v(S_{t+1})\)方向更新\(v(S_t)\)
        \(v(S_t) \leftarrow v(S_t) + \alpha(R_{t+1} + \gamma v(S_{t+1}) - v(S_t))\)
  • TD target：\(\color{green}{R_{t+1} + \gamma v(S_{t+1})}\)
  • TD error：\(\color{green}{\delta = R_{t+1} + \gamma v(S_{t+1}) - v(S_t)}\)
  • 与incremental Monte-Carlo相比
      给定episode \(i\)，用实际return \(G_t\)更新\(v(S_t)\)
        \(v(S_t) \leftarrow v(S_t) + \alpha(G_{i,t} - v(S_t))\)

3.2.2 TD vs. MC

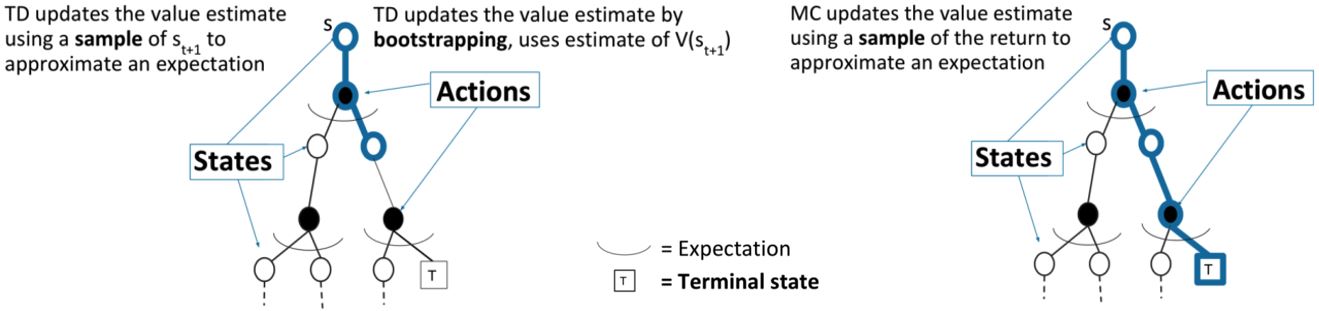
  1. TD可以在每步后在轨学习
    MC必须等到episode结束才能知道return
  2. TD可以从不完全序列中学习
    MC只能从完全序列中学习
  3. TD能用在连续的（non-terminating）环境中
    MC只能用在episodic（terminating）环境中
  4. TD利用马尔可夫性，在马尔可夫环境中更有效
    MC没有利用马尔可夫性，在非马尔可夫环境中更有效
补充

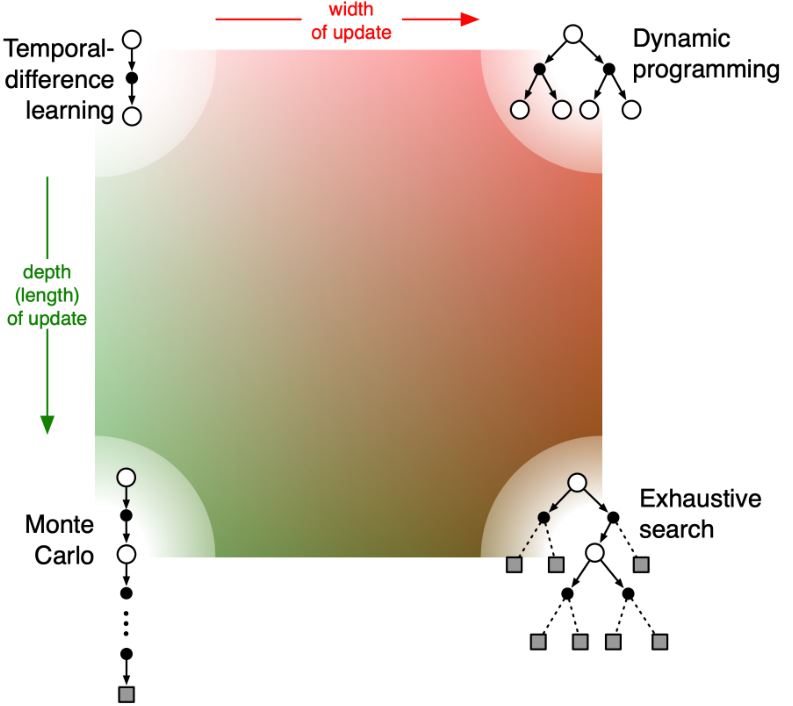
TD方法介于MC和DP之间，既使用了采样的方法，又采用了bootstrapping的方法。

3.2.3 n-step TD

  • n-step TD法是one-step TD和MC的一般情况
  • 可以根据需要平滑地从一个方法转移到另一个，以满足特定任务的需求。

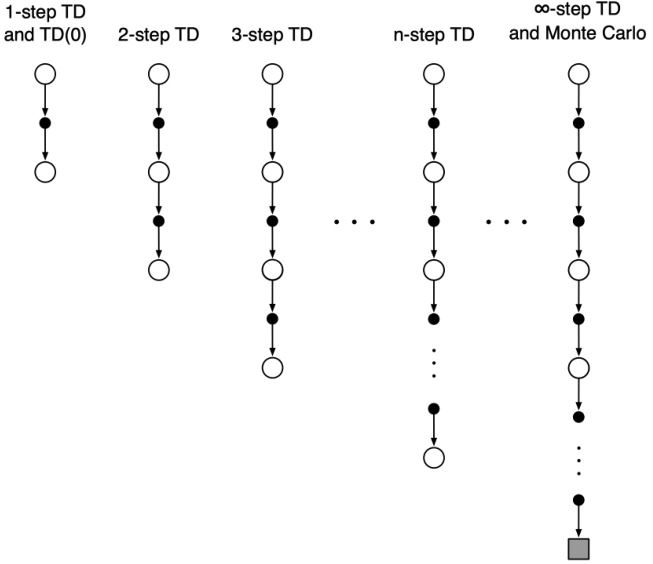
  考虑以下n（\(n = 1, 2, \infty\)）步的return

\[\begin{aligned} n = 1 (TD) \quad & G_t^{(1)} = R_{t+1} + \gamma v(S_{t+1}) \\ n = 2 \quad \quad \quad \ & G_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 v(S_{t+2}) \\ & \vdots \\ n = \infty (MC) \quad & G_t^{\infty} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-t-1} R_T \\ \end{aligned}\]

因此，n-step return被定义为

\[G_t = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n v(S_{t+n})\]

n-step TD：\(v(S_t) \leftarrow v(S_t) + \alpha (G_t^n - v(S_t))\)

Summary for Model-free Prediction

补充

Bootstrapping：更新时涉及估计
DP自助，MC不自助，TD自助
Sampling：更新时对期望采样
DP不采样，MC采样，TD采样

1. Dynamic Programming Backup

\[v(S_t) \leftarrow \mathbb{E}_{\pi} [R_{t+1} + \gamma v(S_{t+1})]\]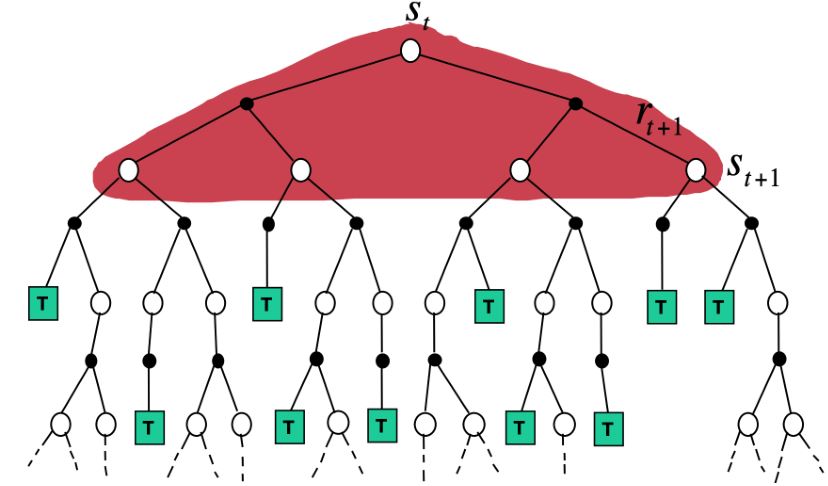

2. Monte-Carlo Backup

\[v(S_t) \leftarrow v(S_t) + \alpha (G_t - v(S_t))\]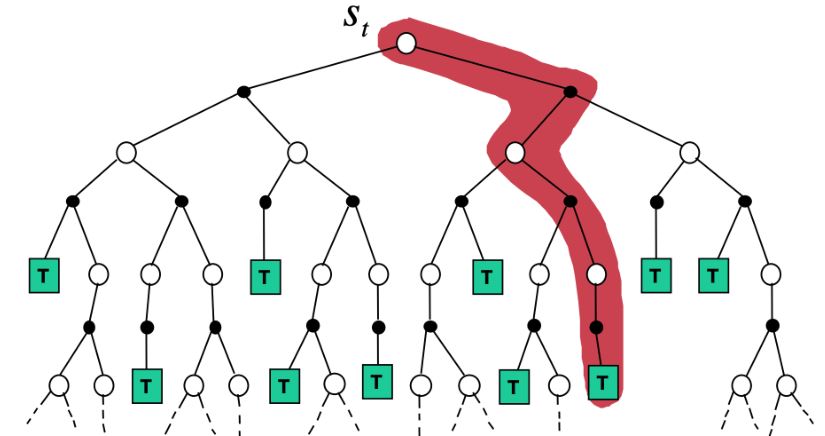

3. Temporal-Difference Backup

\[\text{TD(0): } v(S_t) \leftarrow v(S_t) + \alpha(R_{t+1} + \gamma v(S_{t+1}) - v(S_t))\]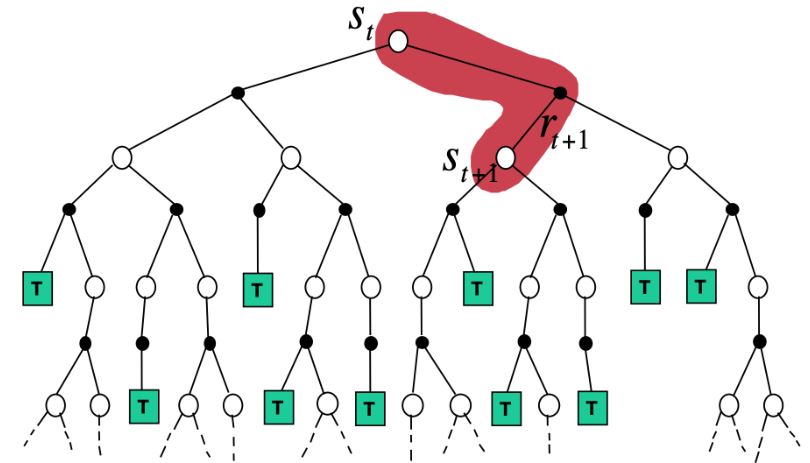

4. Reinforcement Learning

3.3 Monte-Carlo Control

提示

一般涉及到采样时，将策略迭代称为控制。

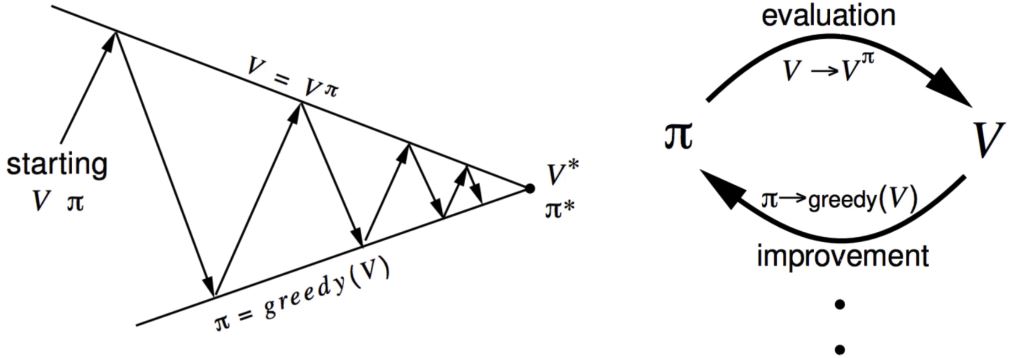
策略迭代，迭代以下两个步骤：

  1. 策略评估（给定当前的\(\pi\)，计算\(v\)）
  2. 策略改进（通过对\(v^{\pi}\)采取贪心行为 \(\pi' = \text{greedy}(v^{\pi})\)）

已知MDP的策略迭代过程：

  1. 计算策略\(\pi\)下的状态-动作价值：\(q_{\pi_i}(s,a) = R(s,a) + \gamma \sum_{s' \in S} P(s' \vert s,a) v_{\pi_i}(s')\)
  2. 对于所有的\(s \in S\)计算新策略\(\pi_{i+1}\)：\(\pi_{i+1}(s) = \text{arg} \max_a q_{\pi_i}(s,a)\) （根据策略改进定理可知，\(\pi_{i+1}\)优于\(\pi_i\)）

问题：如果\(R(s,a)\)和\(P(s' \vert s,a)\)都不可知或不可得怎么办呢？
—利用动作价值函数的广义策略迭代（Generalized Policy Iteration, GPI）

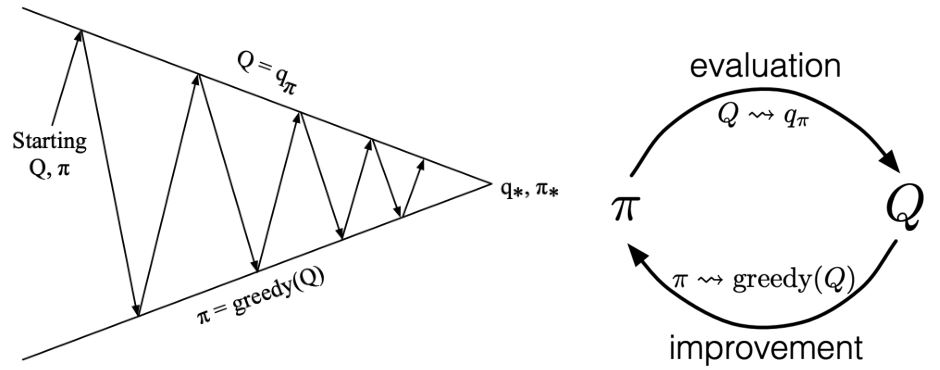
MC控制：

  1. 策略评估：Monte Carlo策略评估 \(Q = q_{\pi}\)
    （采样的两个假设：Ⅰ无限幕 Ⅱ试探性出发假设 ）
  2. 策略改进：贪心策略改进？ \(\pi(s) = \text{arg}\max_a q(s,a)\)

3.3.1 Monte Carlo ES

首次访问型 MC预测，\(v \approx v_{\pi}\)

  • 保证策略迭代收敛的假设：episode有exploring starts
  • Exploring starts可以确保无限频繁地选择所有动作

3.3.2 MC with ϵ-greedy exploration

  • exploration与exploitation的权衡（这部分内容将在后面的课程中详细讨论）
  • ϵ-贪心探索：确保持续探索
\[\pi'(s \vert a) = \begin{cases} \epsilon / |A| + 1 - \epsilon \quad & \text{if } a^* = \text{arg}\max_{a \in A} Q(s,a) \\ \epsilon / |A| & \text{otherwise} \end{cases}\]

所有的动作的概率都是非零的，有\(1 - \epsilon\)的概率选择贪心动作，有\(\epsilon\)的概率随机选择一个动作。

Policy improvement theorem：对于任意的ϵ-贪心策略\(\pi\)，关于\(q_{\pi}\)的ϵ-贪心策略\(\pi\)都是一次改进，\(v_{\pi '}(s) \ge v_{\pi}(s)\)。（证明见书p101式(5.2)）

3.4.3 MC vs. TD 预测与控制

时序差分学习相较于蒙特卡洛有以下优势：

  1. 较小的方差
  2. 在线
  3. 不完全序列

所以可以在控制回路中用TD代替MC

  • 将TD用于\(Q(S,A)\)
  • 用ϵ-贪心策略改进
  • 在每个时间步长更新，而不是等到一次episode结束

3.4 TD Control

首先，回顾一下TD预测：

  一次episode由交替的状态序列和状态-动作对组成

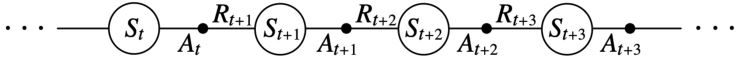
估计价值函数的TD(0)法：
  \(A_t \leftarrow\)由\(\pi\)给出的\(S\)的动作
  采取动作\(A_t\)，观察\(R_{t+1}\)和\(S_{t+1}\)
  \(v(S_t) \leftarrow v(S_t) + \alpha(R_{t+1} + \gamma v(S_{t+1}) - v(S_t))\)

那么，如何估计动作价值函数\(Q(S, A)\)呢？

3.4.1 On-policy vs. Off-policy

On-policy learning：从\(\pi\)中收集的经验来学习策略\(\pi\)
  按非最优的方式行动，以此探索所有动作，然后减少探索，e.g. ϵ-贪心。

另一种重要方法是off-policy learning，使用两个不同的策略：
  一个是正在被学习并成为最优策略的策略
  另一个更具探索性，用于生成轨迹

Off-policy learning：从另一个策略\(\mu\)中采样的经验来学习策略\(\pi\)
  \(\color{green}{\pi}\)：target policy
  \(\color{green}{\mu}\)：behavior policy

3.4.2 Sarsa: On-policy

  一次episode是由交替的状态序列和状态-动作对组成的。

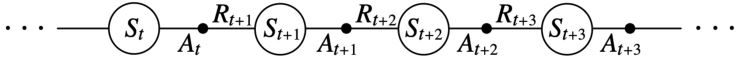
  One-setp Sarsa: 一步ϵ-贪心策略，然后bootstrap状态价值函数：

\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \big[ R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \big]\]

每次从非终止状态\(S_t\)转换后完成更新。

  TD target \(R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})\)

n-step Sarsa

  考虑以下n（\(n = 1, 2, \infty\)）步的Q-returns

\[\begin{aligned} n = 1 (Sarsa) \quad & q_t^{(1)} = R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) \\ n = 2 \quad \quad \quad \ & q_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 Q(S_{t+2}, A_{t+2}) \\ & \vdots \\ n = \infty (MC) \quad & q_t^{\infty} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-t-1} R_T \\ \end{aligned}\]

因此，n-step Q-return被定义为

\[q_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n Q(S_{t+n}, A_{t+n})\]

n-step Sarsa用n-step Q-return更新\(Q(s,a)\)：\(Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (q_t^{(n)} - Q(S_t, A_t))\)

Expected Sarsa

\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (R_{t+1} + \gamma \mathbb{E}_{\pi}[Q(S_{t+1}, a \vert S_{t+1})] - Q(S_t, A_t))\]
  1. 默认情况下\(\pi = \mu\)，同轨。
  2. 若\(\pi\)是贪心策略，即\(\pi = \text{arg} \max_a Q(S_{t+1}, a) = a^*\)，此时期望Sarsa为离轨策略，会退化成Q-learning。

3.4.3 Q-learning: Off-policy

Off-policy control遵循以下行为策略\(\mu(a \vert s)\)来收集数据
  \(S_1, A_1, R_2, \ldots, S_T \sim \mu\)
  用\(S_1, A_1, R_2, \ldots, S_T\)更新\(\pi\)

离轨学习的好处：

  1. 在遵循探索性策略的同时学习最优策略
  2. 通过观察人或其它agents来学习
  3. 重用由旧策略\(\pi_1, \pi_2, \ldots, \pi_{t-1}\)生成的经验

Off-policy control with Q-learning：

  • 行为价值\(Q(s, a)\)的离轨学习
  • 无需重要性采样
  • TD目标中的下一个动作是从备选动作\(A' \sim \pi(. \vert S_t)\)中选择的
  • 将\(Q(S_t, A_t)\)更新为备选动作的值
    \(Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (R_{t+1} + \gamma Q(S_{t+1}, A') - Q(S_t, A_t))\)

  Q-learning中行为策略和目标策略都是允许改进的。目标策略\(\color{blue}{\pi}\)对\(\color{blue}{Q(s, a)}\)贪心

\[\pi(S_{t+1}) = \text{arg}\max_{a'} Q(S_{t+1}, a')\]

其中，行为策略\(\color{blue}{\mu}\)可以是完全随机的，但是我们让它随着对\(\color{blue}{Q(s, a)}\)的ϵ-贪心而改进。

  因此，Q-learning的目标为

\[\begin{aligned} R_{t+1} + \gamma Q(S_{t+1}, A') & = R_{t+1} + \gamma Q(S_{t+1}, \text{arg}\max_{a'} Q(S_{t+1}, a')) \\ & = R_{t+1} + \gamma \max_{a'} Q(S_{t+1}, a') \end{aligned}\]

Q-learning的更新过程为

\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \big[ R_{t+1} + \gamma \max_{a} Q(S_{t+1}, a) - Q(S_t, A_t) \big]\]

3.4.4 Sarsa vs. Q-learning

Sarsa: on-policy TD control
  按ϵ-贪心，用从\(Q\)派生的策略从\(S_t\)选择动作\(A_t\)
  采取行为\(A_t\)，观察\(R_{t+1}\)和\(S_{t+1}\)
  按ϵ-贪心，用从\(Q\)派生的策略从\(S_{t+1}\)选择动作\(A_{t+1}\)
  \(Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \big[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \big]\)

Q-learning: off-policy TD control
  按ϵ-贪心，用从\(Q\)派生的策略从\(S_t\)选择动作\(A_t\)
  采取行为\(A_t\)，观察\(R_{t+1}\)和\(S_{t+1}\)
  然后将\(A_{t+1}\)"想象"为更新目标中的\(\text{arg}\max_{a'} Q(S_{t+1}, a')\)
  \(Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \big[R_{t+1} + \gamma \max_{a} Q(S_{t+1}, a) - Q(S_t, A_t)\big]\)

Sarsa和Q-learning的回溯图

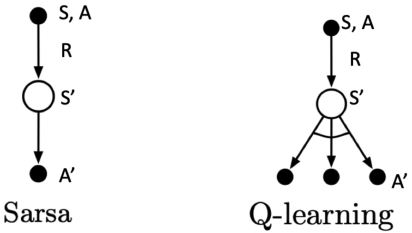
  在Sarsa中，\(A\)和\(A'\)都是从同一个策略中采样得到的，所以它是on-policy的；在Q-learning中，\(A\)和\(A'\)是从不同的策略中得到的，\(A\)更具探索性而\(A'\)是直接通过取最大值的操作得到的。

例：Cliff Walk（书 Example 6.6）
  Sarsa和Q-learning的例子

3.4.5 DP vs. TD

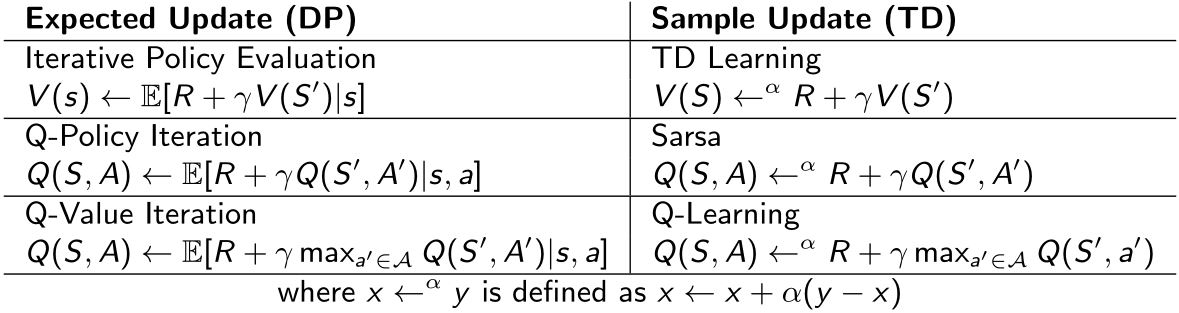
Summary

无模型预测

  • 在不知道MDP模型的情况下，只通过与环境交互来评估状态价值

MDP的无模型控制

  • 无模型控制：优化一个未知MDP的价值函数
  • 利用MC和TD的广义策略迭代

Supplement：Importance Sampling

  估计一个函数的期望为\(E_{x \sim P}[f(x)] = \int{f(x) P(x) dx} \approx \frac{1}{n} \sum_i f(x_i)\)，但是有时很难从\(P(x)\)中采样\(x\)，可以从另一个分布\(Q(x)\)中对\(x\)采样，然后修改权重

\[\begin{aligned} \mathbb{E}_{x \sim P}[f(x)] & = \int{P(x) f(x) dx} \\ & = \int{Q(x) \frac{P(x)}{Q(x)} f(x) dx} \\ & = \mathbb{E}_{x \sim Q} \bigg[\frac{P(x)}{Q(x)} f(x)\bigg] \approx \frac{1}{n} \sum_i \frac{P(x_i)}{Q(x_i)} f(x_i) \end{aligned}\]

  离轨RL的重要性采样：用从另一个策略（行为策略）采样的轨迹来估计回报的期望

\[\begin{aligned} \mathbb{E}_{T \sim \pi}[g(T)] & = \int{P(T) g(T) dT} \\ & = \int{Q(T) \frac{P(T)}{Q(T)} g(T) dT} \\ & = \mathbb{E}_{T \sim \mu} \bigg[\frac{P(T)}{Q(T)} g(T)\bigg] \approx \frac{1}{n} \sum_i \frac{P(T_i)}{Q(T_i)} g(T_i) \end{aligned}\]

离轨MC的重要性采样

  1. 根据行为策略\(\mu\)生成episode，并计算生成的return \(G(t)\)，即\(S_1, A_1, R_2, \ldots, S_T \ \sim \ \mu\)。
  2. 根据策略之间的相似性返回权重\(G_t\)，在整个情节中乘以重要性采样校正
    \(G_t^{\pi / \mu} = \frac{\pi (A_t \vert S_t)}{\mu (A_t \vert S_t)} \frac{\pi (A_{t+1} \vert S_{t+1})}{\mu (A_{t+1} \vert S_{t+1})} \cdots \frac{\pi (A_T \vert S_T)}{\mu (A_T \vert S_T)} G_t\)
  3. 用矫正后的return更新价值函数 \(V(S_t) \leftarrow V(S_t) + \alpha (G_t^{\pi / \mu} - V(S_t))\)

离线TD的重要性采样

  1. 根据行为策略\(\mu\)生成的TD目标来评估\(\pi\)
  2. 根据重要性采样来加权TD目标\(R + \lambda V(S')\)
  3. 只需要一次重要性采样校正
    \(V(S_t) \leftarrow V(S_t) + \alpha \left(\frac{\pi (A_t \vert S_t)}{\mu (A_t \vert S_t)} (R_{t+1} + \lambda V(S_{t+1})) - V(S_t)\right)\)
  4. 策略只要在一个步骤中是相似的即可
补充

为什么不对Q-learning使用重要性采样？
— 简单来说是因为Q-learning不对策略分布进行期望值估计。

  价值迭代中的贝尔曼最优性回溯为\(Q(s, a)= R(s, a) + \gamma \sum_{s' \in S} {P(s' \vert s,a) \max_{a'} {Q(s', a')}}\)。Q-learning可以被认为是价值迭代的基于采样的版本，使用从环境中收集的样本而不是使用过渡动态的期望值

\[Q(s, a) = r + \gamma \max_{a'} {Q(s', a')}\]

Q-learning是在转换分布上，而不是在策略分布上，因此不需要修正不同的策略分布。