Proximal Policy Optimization

Proximal Policy Optimization AlgorithmsJohn Schulman, F. Wolski, P. Dhariwal, A. Radford and O. Klimov, 2017

摘要——文章提出了一类新的用于强化学习的策略梯度方法，在通过与环境交互采样数据时交替，并使用随机梯度上升优化一个"替代"目标函数。在标准策略梯度方法中每次采样都会进行一次梯度更新，本文提出了一种新的目标函数，使得在多个epochs用minibatch更新成为可能。新方法称为proximal policy optimization (PPO)，具有TRPO的部分优点，但更易于实现，更一般化，且有更好的采样复杂度（从经验上来说）。实验表明，PPO优于其它在线策略梯度方法，总体上在采样复杂度、简洁性和延迟时间之间取得了良好的平衡。

1 Introduction

  利用神经网络作函数逼近器的强化学习中，主要的方法有deep Q-learning、原始的策略梯度方法和置信域/自然梯度方法。但是，在以下方面还有改进空间：可扩展性（拓展到大的模型和并行实现）、数据高效和鲁棒性（i.e. 无需调超参数即可胜任不同任务）。

  本文试图介绍一种算法，该算法在只使用一阶优化的情况下，达到TRPO的数据效率和可靠性能。我们提出了一个新的截断概率比（clipped probability ratios）目标，形成了对策略表现的悲观估计（i.e. 下界）。为了优化策略，我们在从策略中采样数据和对采样数据进行多次优化之间进行交替。

  实验对比了不同的替代目标，发现截断概率比目标最好。与其它方法相比，PPO在连续控制任务中表现得比其它方法好。在Atari中，（在样本复杂度上的）性能显著地比A2C好，且与ACER相当，但PPO更简单。

2 Background

2.1 Policy Gradient Methods

  策略梯度方法计算策略梯度的估计量，并将其插入到随机梯度上升算法中。虽然提倡使用相同的轨迹对目标函数进行多步优化，但这样做的理由并不充分，而且在经验上往往会导致破坏性的大的策略更新。

2.2 Trust Region Methods

  TRPO中，在策略更新大小的约束下最大化目标函数（"替代"目标）。在论证TRPO时，实际使用的是惩罚项而不是约束条件。这源于某个替代目标（它计算状态上的最大KL而不是均值）对策略\(\pi\)的性能形成了一个下界。TRPO用硬约束来代替惩罚项是因为很难选择合适的罚系数\(\beta\)，固定的\(\beta\)无法胜任不同的问题，甚至在一个简单的问题上都可能效果不好。要想用一阶算法来模拟TRPO的单调改进很难，选择一个固定的罚系数并用SGD来优化"替代"目标函数是不够的，还需要更多修饰。

3 Clipped Surrogate Objective

  用\(r_t(\theta)\)表示概率比值\(r_t(\theta) = \frac{\pi_{\theta}(a_t \vert s_t)}{\pi_{\theta_{\text{old}}}(a_t \vert s_t)}\)，所以有\(r_t(\theta_{\text{old}}) = 1\)。TRPO最大化的"替代"目标即

\[L^{\text{CPI}}(\theta) = \hat{\mathbb{E}}_t \left[ \frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{\text {old }}}(a_t \mid s_t)} \hat{A}_t \right] = \hat{\mathbb{E}}_t\left[r_t(\theta) \hat{A}_t\right]\]

上标CPI表示conservative policy iteration（保守策略迭代）。在没有约束条件的情况下，最大化这个目标函数会带来非常大的策略更新，所以下面我们需要修饰这个目标，惩罚那些让\(r_t(\theta)\)远离1的策略变化。

  我们提出了如下目标函数：

\[\color{green}{ L^{\text{CLIP}}(\theta) = \hat{\mathbb{E}}_t \left[ \min \left( r_t(\theta) \hat{A}_t, \operatorname{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_t \right) \right] }\]

其中\(\epsilon\)是一个超参数，这里\(\epsilon = 0.2\)。\(\min\)函数中第一项即\(L^{\text{CPI}}\)。第二项\(\operatorname{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_t\)通过截断概率比值的方式修饰了"替代"目标，移除了将\(r_t\)移出\([1-\epsilon, 1+\epsilon]\)的激励。通过取截断目标和未截断目标中更小的，就可以得到未截断目标的一个下界。通过这个机制，我们可以忽略让目标更好的概率比的变化，但是考虑让目标更差的概率比的变化。注意，在\(\theta_{\text{old}}\)附近\(L^{\text{CLIP}} = L^{\text{CPI}}\)一阶成立，但是\(\theta\)离开\(\theta_{\text{old}}\)后就不成立了。注意，概率比在\(1-\epsilon\)处还是\(1+\epsilon\)处截断取决于adavantage \(\hat{A}_t\)的正负。下图是\(L^{\text{CLIP}}\)中的一项（i.e. 某个时刻\(t\)），整个\(L^{\text{CLIP}}\)是很多这样的项的和。

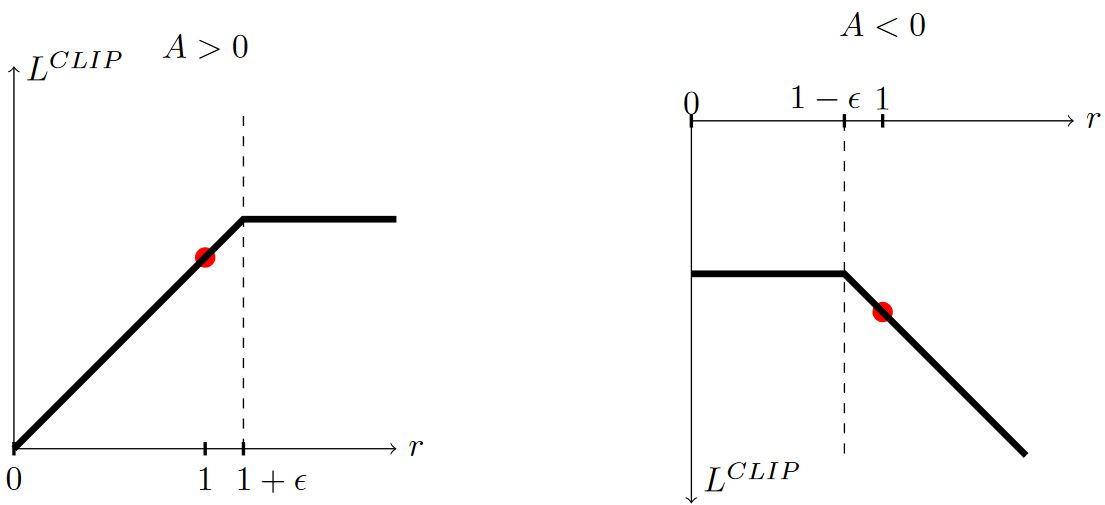
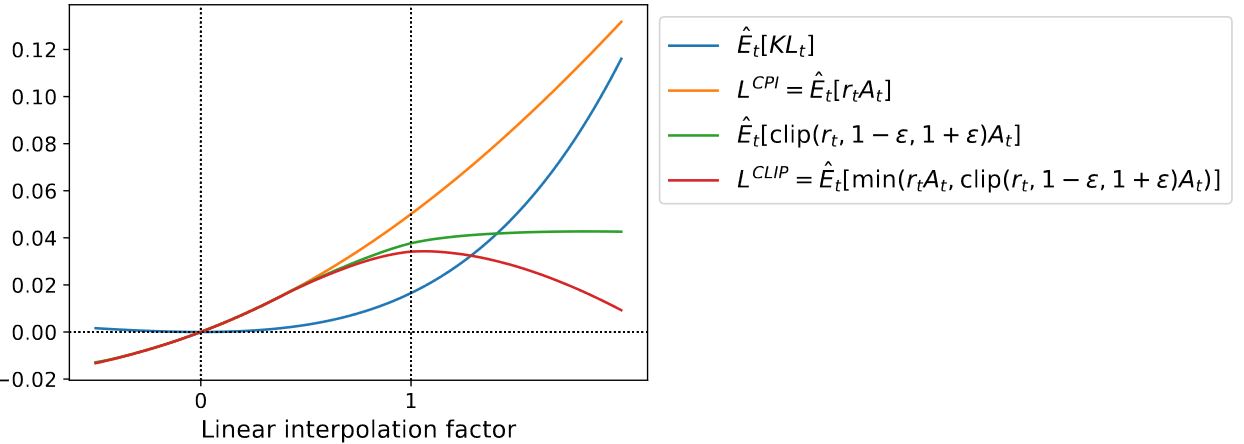
  下图是"替代"目标\(L^{\text{CLIP}}\)另一种直觉来源，展示了在一个连续的控制问题上通过近端策略优化（我们将简要介绍的算法）得到的沿策略更新方向插值时，几个目标是如何变化的。

4 Adaptive KL Penalty Coefficient

  另一种可以代替或者作为补充的方法，就是对KL散度加惩罚项，并且自适应地调整惩罚项的系数，使得每次策略更新的时候可以达到某个期望的KL散度值\(d_{\text{targ}}\)。在我们的实验中，KL惩罚项的性能不如截断代替目标，但该方法是一个重要的baseline，所以我们没有省略。

  该算法的最简单示例，在每次策略更新的时候进行以下操作:

• 用minibatch SGD的几个epoch，优化含KL惩罚的目标
    \(L^{K L P E N}(\theta)=\hat{\mathbb{E}}_t\left[\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{\text {old }}}\left(a_t \mid s_t\right)} \hat{A}_t-\beta \operatorname{KL}\left[\pi_{\theta_{\text {old }}}\left(\cdot \mid s_t\right), \pi_\theta\left(\cdot \mid s_t\right)\right]\right]\)
• 计算\(d=\hat{\mathbb{E}}_t\left[\mathrm{KL}\left[\pi_{\theta_{\text {old }}}\left(\cdot \mid s_t\right), \pi_\theta\left(\cdot \mid s_t\right)\right]\right]\)
  — If \(d \lt d_{\text{targ}}/1.5\), \(\beta \leftarrow \beta /2\)
  — If \(d \gt d_{\text{targ}} \times 1.5\), \(\beta \leftarrow \beta \times 2\)

更新的\(\beta\)用于下一次策略更新。根据这个方案，策略更新时KL散度很少会与\(d_{\text{targ}}\)相差很大。这种相差很大的情况只会偶尔发生，而且\(\beta\)会迅速调整过来。上面的参数1.5和2都是启发式选择的，但是算法本身对它们并不敏感。\(\beta\)的初值是另一个超参数，但在实际使用是并不重要，因为算法本身会很快调整它。

5 Algorithm

  前面章节提到的surrogate losses可以通过在典型的策略梯度实施的基础上小幅变化得到计算和微分。对于那些使用自动微分的实现，一个是简单构造loss \(L^{CLIP}\)或\(L^{KLPEN}\)来代替\(L^{PG}\)，一个是在这个目标上执行多步随机梯度上升。

  大多是可减小方差的advantage函数估计器的计算技巧都利用了一个学过的state-value函数\(V(s)\)。如果用策略和价值函数参数共享的网络结构，我们就必须用结合了策略surrogate和价值函数误差项的loss function。这个目标函数还可以进一步增广，比如增加一项熵bonus以保证充分探索。将这些项结合起来，得到如下目标：

\[L_t^{CLIP + VF + S}(\theta) = \hat{\mathbb{E}}_t \left[ L_t^{C L I P}(\theta)-c_1 L_t^{V F}(\theta)+c_2 S\left[\pi_\theta\right]\left(s_t\right) \right]\]

其中，\(c_1, c_2\)为系数，\(S\)为熵bonus，\(L_t^{V F}\)为方差loss \((V){\theta}(s_t) - V_t^{targ})^2\)。

  策略梯度实现的一种类型，非常适合与递归神经网络一起使用，每\(T\)个时间步长运行策略一次（\(T\)远小于episode长度），并用收集到的样本进行一次更新。这类实现需要一个视野不超过\(T\)的advantage估计器，比如

\[\hat{A}_t = -V(s_t) + r_t + \gamma r_{t+1} + \cdots + \gamma^{T-t+1} r_{T-1}+\gamma^{T-t} V(s_T)\]

其中，\(t\)表示在给定的T长度的序列片段\([0,T]\)内的时间索引。写出advantage估计的一般形式，该式会在\(\lambda = 1\)的时候退化成上式。

\[\hat{A}_t = \delta_t+(\gamma \lambda) \delta_{t+1}+\cdots+\cdots+(\gamma \lambda)^{T-t+1} \delta_{T-1}, \text{ where } \delta_t=r_t+\gamma V\left(s_{t+1}\right)-V\left(s_t\right)\]

  采用定长轨迹片段的PPO算法如上所示。每次迭代，\(N\)个（并行）中的每个actor收集\(T\)时间步长的数据。然后，基于这\(NT\)个时间步长的数据构造surrogate loss，并用minibatch SGD对\(K\)个epochs进行优化。