MM & HMM

应用背景：
  天气预报：下雨、晴天、多云……
  预测传染病的感染
  语音识别
  中文输入法
  人口预测
  生物信息学（e.g. 基因分析）
  ……

3.1 Markov Model

例：天气预报问题

  • 三种天气状态：{晴天，雨天，雾天}
  • 今天的天气情况与昨天、前天、……的天气有关，\(P(w_n \vert w_{n-1},w_{n-2},\ldots,w_1)\)
  • 如果已知过去三天的情况（按顺序）：晴天，晴天，雾天
  • 那么明天是雨天的概率：\(P(w_4 = \text{雨天} \vert w_3 = \text{雾天} ,w_2 = \text{晴天} ,w_1 = \text{晴天} )\)

3.1.1 马尔可夫模型

注意

一下讨论均基于一阶马尔可夫假设

  • 给定一系列数据 \(D = \{ x_1,x_2,x_3,\ldots,x_N \}\)
  • 一阶马尔可夫假设
    在\(n\)时刻观察的概率仅取决于在\(n-1\)时刻的观察。
    \(p(x_n \vert x_{n-1}, \ldots, x_2, x_1)\) \(p(D \vert M) = p(x_1) \prod_{n=2}^N p(x_n \vert x_{n-1})\)
  • 转移概率\(\color{green}{a_{i,j}}\)
    给定\(n-1\)时刻的状态\(S_i\)，\(n\)时刻处于状态\(S_j\)的概率 \(a_{i,j} = p(x_n = S_j \vert x_{n-1} = S_i)\)

3.1.2 转移概率的性质

  1. 非负性 \(a_{i,j} \ge 0\)
  2. Time invariant (homogeneous 时间不变性)
    \(p(x_n = S_j \vert x_{n-1} = S_i) = p(x_{n+T} = S_j \vert x_{n-1+T} = S_i)\)
  3. 转移矩阵：每行之和 = 1
    \(\mathbf{A} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \qquad \sum_{j=1}^M {a_{i,j}} = 1 \text{ for } i = 1,\ldots,M\)

例

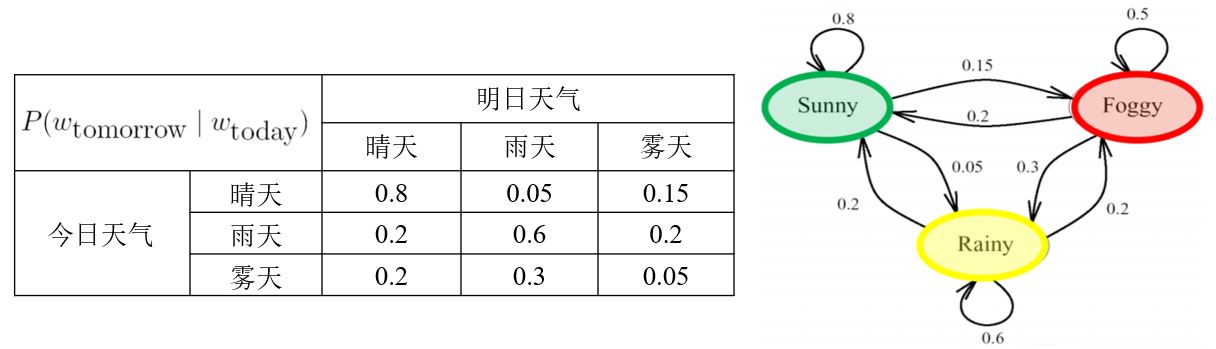
利用Markov假设：\(P(w_n \vert w_{n-1},w_{n-2},\ldots,w_1) \approx P(w_n \vert w_{n-1})\)
以及联合概率：\(P(w_1,\ldots,w_n) = \prod_{i=1}^n P(w_i \vert w_{i-1})\)

Q1：已知今天是晴天，那么明天是晴天且后天下雨的概率是多少？
Q2：已知今天是雾天，那么后天下雨的概率是多少？

3.2 Hidden Markov Model

什么是隐马尔可夫模型（HMM）？

例：天气预测问题
  假设一个人被关在一个房间里几天，他想知道外面的天气。
  他所能知道的唯一线索：看守者是否拿着伞。

  • 观察到的状态：伞？
  • 隐藏的状态：天气

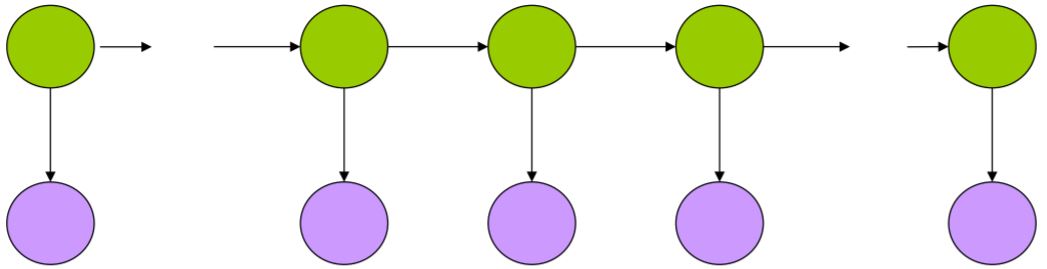
  图形模型
  圆圈：状态
  箭头：状态之间的依赖关系

  绿色圆圈：hidden states
  只由前一个状态决定
  未来与过去无关，只与现在有关。

  紫色圆圈：observed states
  观察到的状态只与隐状态有关

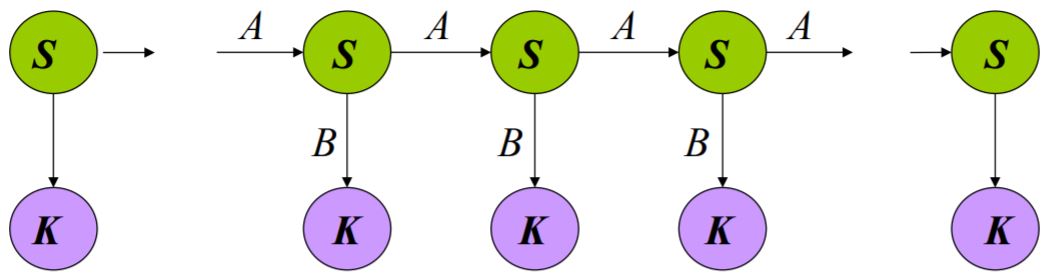
  \(\{ S,K,\prod,A,B \}\)
  \(S: \{ s_1, \ldots, s_N \}\) 隐状态的值
  \(K: \{ k_1, \ldots, k_M \}\) 观察状态的值
  \(\prod = \{\pi_i\}\) 初始状态概率
  \(A = \{ a_{ij} \}\) 状态转移概率 \(p(x_n=S_j \vert x_{n-1}=S_i) = a_{ij}\)
  \(B = \{ b_{ij} \}\) 观察状态概率（输出概率） \(p(y_n=K_j \vert x_n=S_i) = b_{ij}\)

例：之前的天气Markov过程为\(P(w_1,\ldots,w_n) = \prod_{i=1}^n P(w_i \vert w_{i-1})\)，而现在实际的天气情况被隐藏了，我们只能观察到看守者是否带了雨伞

\[P(w_1,\ldots,w_n \vert u_1,\ldots,u_n) = \frac {P(u_1,\ldots,u_n \vert w_1,\ldots,w_n) P(w_1,\ldots,w_n)} {P(u_1,\ldots,u_n)}\]

其中，如果看守者在第\(i\)天带了伞，那么\(u_i\)为真，如果没有则为假。

3.2.1 输出独立性假设

  假设对于所有的\(i\)，已知\(w_i\)，那么对于所有的\(j \neq i\)，\(u_i\)与所有的\(u_j\)和\(w_j\)无关。

\[P(u_1,\ldots,u_n \vert w_1,\ldots,w_n) = \prod_{i=1}^n P(u_i \vert w_i)\]

Q3：观察变量有两种取值\(\{ C1 = \text{带伞} , C2 = \text{没带伞} \}\)
  隐变量有三种状态\(\{ S_1 = \text{晴天} , S_2 = \text{雨天} ,S_1 = \text{雾天} \}\)
假设被关进房间的第一天是晴天，第二天看守者带了伞，那么第二天下雨的概率是多少？

\[\begin{aligned} & p(x_2=S_2 \vert y_2=C_1 , x_1=S_1) \\ = & p(x_2=S_2 \vert x_1=S_1) * p(y_2=C_1 \vert x_2=S_2) / p(y_2=C_1 \vert x_1=S_1) \end{aligned}\]

3.2.2 基本问题

  给定初始HMM \(\mu = \{ A,B,\prod \}\)，观察序列为\(O = o_1,\ldots,o_T\)

  • Estimation problem

    计算给定观察序列的概率\(p(O \vert \mu)\)

  • Decoding problem

    给定一个观察序列，计算最有可能的隐状态序列

  • Learning problem

    给定一个观察序列和可能模型的集合，哪个模型与数据最接近。

1. Estimation prob.

  \(O = o_1,\ldots,o_T\)，\(\mu = \{ A,B,\prod \}\)，计算\(P(O \vert \mu)\)

Solution 1

\[P(O \vert \mu) = \sum_X P(O,X \vert \mu)\]

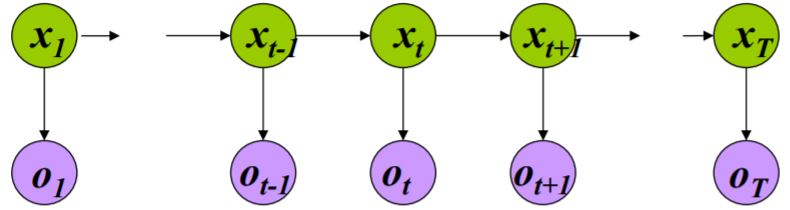
其中，\(P(O, X \vert \mu) = P(O \vert X, \mu) P(X \vert \mu)\)，所以

\[P(O \vert \mu) = \sum_X P(O \vert X, \mu) P(X \vert \mu)\]

其中，\(P(O \vert X, \mu) = b_{x_1 o_1} b_{x_2 o_2} \cdots b_{x_T o_T}\)，\(P(X \vert \mu) = \pi_{x_1} a_{x_1 x_2} a_{x_2 x_3} \cdots a_{x_{T-1} a_T}\)

\[\boxed{ P(O \vert \mu) = \sum_{\{ x_1 \ldots x_T \}} { \pi_{x_1} b_{x_1 o_1} \prod_{t=1}^{T-1} a_{x_t x_{t+1}} b_{x_{t+1} o_{t+1}} } }\]

方法1需要列出所有可能的状态序列（\(\text{长度} = T\)），需要做\(2TN^T\)次乘法（共\(N\)种可能的状态）。

Solution 2: Foward algorithm

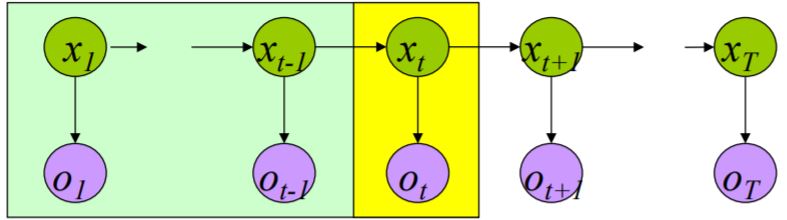
HMM特殊的结构为动态规划提供了一种有效的解决方案——前向算法。

  定义\(\quad \quad \color{green}{ \alpha_t(i) = P(o_1 \cdots o_t, x_t=i \vert \mu) }\) \(\quad \rightarrow \quad P(O \vert \mu) = \sum_{i=1}^N \alpha_T(i)\)

\[\begin{aligned} \alpha_{t+1}(j) & = P(o_1 \cdots o_{t+1}, x_{t+1}=j \vert \mu) \\ & = \sum_{i=1 \ldots N} P(o_1 \cdots o_{t}, o_{t+1}, x_t=i, x_{t+1}=j) \\ & = \sum_{i=1 \ldots N} P(o_1 \cdots o_{t}, o_{t+1}, x_{t+1}=j \vert x_t=i)P(x_t=i) \\ & = \sum_{i=1 \ldots N} P(o_1 \cdots o_{t} \vert x_t=i) P(o_{t+1}, x_{t+1}=j \vert x_t=i) P(x_t=i) \\ & = \sum_{i=1 \ldots N} P(o_1 \cdots o_{t} \vert x_t=i) P(x_{t+1}=j \vert x_t=i) P(o_{t+1} \vert x_{t+1}=j) \\ & = \sum_{i=1 \ldots N} \alpha_t(i) a_{ij} b_{j O_{t+1}} \end{aligned}\] \[\boxed { P(O \vert \mu) = \sum_{i=1}^N \alpha_T(i) }\]

  \(P(O \vert \mu)\)：\(O(N^2 T)\)乘法

Solution 3: Backard algorithm

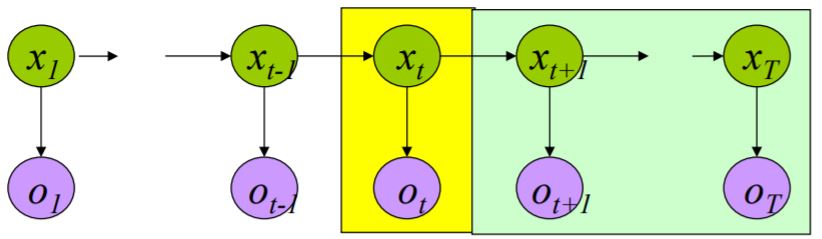
  定义\(\quad \quad \color{green}{ \beta_t(i) = P(o_t \cdots o_T \vert x_t=i , \mu) }\) \(\quad \rightarrow \quad\boxed{ P(O \vert \mu) = \sum_{i=1}^N \pi_i \beta_1(i) }\)

\[\begin{aligned} & \beta_t(i) = \sum_{j=1 \ldots N} a_{ij} b_{i O_t} \beta_{t+1}(j) \quad , t = T,T-1,\ldots,1 \quad 1 \le i \le N \\ & \beta_{T+1}(i) = 1 \quad , \ 1 \le i \le N \end{aligned}\]

总结

  枚举法 \(P(O \vert \mu) = \sum_{\{ x_1,\ldots,x_T \}} {\pi_{x_1} b_{x_1 o_1} \prod_{t=1}^{T-1} a_{x_t x_{t+1}} b_{x_{t+1} o_{t+1}} }\)

  前向法 \(P(O \vert \mu) = \sum_{i=1}^N \alpha_T(i)\)

  后向法 \(P(O \vert \mu) = \sum_{i=1}^N \pi_i \beta_1(i)\)

2. Decoding prob.

  • 给定一个观察序列，计算最有可能的隐状态序列。
  • 找出最能解释观测结果的状态序列。
  • 可能有多个\(X\)使得\(P(X \vert O)\)取到最大。

Viterbi algorithm

注意

维特比算法找到的可能是局部最优值。

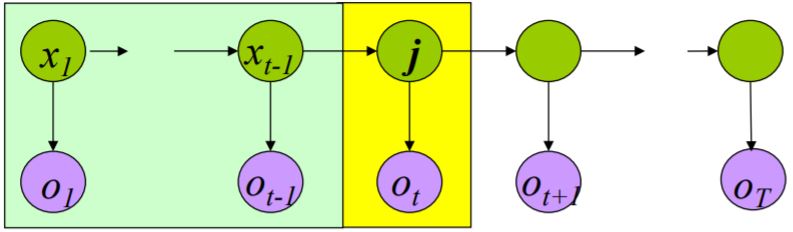
定义

\[\delta_t(j) = \max_{x_1 \ldots x_{t-1}} P( x_1 \ldots x_{t-1} , o_1 \ldots o_{t-1} x_t = j , o_t )\] \[\max_x P(X \vert O) \Leftrightarrow \max_x P(X , O) \Leftrightarrow \max_j \delta_T(j)\]
\[\delta_{t+1}(j) = \max_i \{ \delta_t(i) a_{ij} b_{j o_{t+1}} \}\] \[\psi_{t+1}(j) = \mathop{argmax}_i \{ \delta_t(i) a_{ij} b_{j o_{t+1}} \}\]

其中，\(\psi_{t+1}(j)\)为预测的\(t+1\)时刻隐状态，即\(\hat{X}_{t+1}\)

3.2.3 HMM应用

  • 语音识别
  • （中/日）输入法
  • 词性标注
  • 基因分析
  • 任何线性序列的现象