Plicy Optimization Ⅱ: SOTA

Policy Gradient→Natural Policy Gradient/TRPO→ACKTR→PPO
TRPO: Trust region policy optimization. Schulman, L., Moritz, Jordan, Abbeel. 2015
ACKTR: Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation. Y. Wu, E. Mansimov, S. Liao, R. Grosse, and J. Ba. 2017
PPO: Proximal policy optimization algorithms. Schulman, Wolski, Dhariwal, Radford, Klimov. 2017
Q-learning→DDPG→TD3→SAC
DDPG: Deterministic Policy Gradient Algorithms, Silver et al. 2014
TD3: Addressing Function Approximation Error in Actor-Critic Methods, Fujimoto et al. 2018
SAC: Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor, Haarnoja et al. 2018

注意

这章的内容非常有挑战性，建议先阅读论文。

6.0 Review

6.0.1 Value-based VS Policy-based

在基于价值的RL确定性策略是直接对价值函数作\(a_t = \operatorname{argmax}_a Q(s_t,a)\)贪心运算得到的。
在策略优化中，我们有来自\(\pi_{\theta}(a \vert s)\)随机的策略输出，其中\(\theta\)是要优化的策略参数。

策略目标函数为\(J(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta}} [R(\tau)]\)，
策略梯度（REINFORCE）为\(\nabla_{\theta} J(\theta) =\mathbb{E}_{\pi_{\theta}}\left[G_{t} \nabla_{\theta} \log \pi_{\theta}(s, a)\right] \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T-1} G_{t}^{i} \nabla_{\theta} \log \pi_{\theta}\left(s_{i}, a_{i}\right)\)。

6.0.2 Advantage Actor-Critic

引入baseline来减小AC的方差

Advantage function将\(Q\)与baseline \(V\)结合：

\[A^{\pi}(s,a) = Q^{\pi}(s,a) - V^{\pi}(s)\]

那么策略梯度变为：

\[\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} [\nabla_{\theta} \log \pi_{\theta}(s,a) A^{\pi_{\theta}}(s,a)]\]

两个函数逼近器包含两组参数向量，利用TD learning或MC来更新这两组参数

\[\begin{aligned} V_{\mathbf{v}}(s) & \approx V^{\pi}(s) \\ Q_{\mathbf{w}}(s,a) & \approx Q^{\pi}(s,a) \end{aligned}\]

对于真价值函数\(V^{\pi_{\theta}}(s)\)，其TD error \(\delta^{\pi_{\theta}} = r(s,a) + \gamma V^{\pi_{\theta}}(s') - V^{\pi_{\theta}}(s)\)，是优势函数的估计值。

\[\begin{aligned} \mathbb{E}_{\pi_{\theta}}\left[\delta^{\pi_{\theta}} \mid s, a\right] &= \mathbb{E}_{\pi_{\theta}}\left[r+\gamma V^{\pi_{\theta}}\left(s^{\prime}\right) \mid s, a\right]-V^{\pi_{\theta}}(s) \\ &= Q^{\pi_{\theta}}(s, a)-V^{\pi_{\theta}}(s) \\ &= A^{\pi_{\theta}}(s, a) \end{aligned}\]

所以，我们可以用TD error来计算策略梯度

\[\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} [\nabla_{\theta} \log \pi_{\theta}(s,a) \delta^{\pi_{\theta}}]\]

这样，只要一组由TD估计的critic参数\(\color{red}{\kappa}\)就可以了

\[\delta_{\mathbf{v}} = r + \gamma V_{\kappa}(s') - V_{\kappa}(s)\]

6.0.3 Different time-scales

Crtic at different time-scales

Critic可以从以下多个目标来估计线性价值函数\(V_{\kappa}(s) = \psi(s)^T \kappa\)：
对于MC，其更新为\(\Delta \kappa = \alpha(\color{green}{G_t} \color{black}{-} V_{\kappa}(s)) \psi(s)\)
对于TD(0)，其更新为\(\Delta \kappa = \alpha(\color{green}{r + \gamma V_{\kappa}(s')} \color{black}{-} V_{\kappa}(s)) \psi(s)\)
对于k-step return，其更新为\(\Delta \kappa = \alpha(\color{green}{\sum_{i=0}^k \gamma^i r_{t+i} + \gamma^k V_{\kappa}(s_{t+k})} \color{black}{-} V_{\kappa}(s)) \psi(s)\)

Actors at different time-scales

策略梯度\(\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} [\nabla_{\theta} \log \pi_{\theta}(s,a) A^{\pi_{\theta}}(s,a)]\)也可以在许多时间尺度上进行估计：
Monte-Carlo Actor-Critic策略梯度用整个return的误差来估计，\(\nabla_{\theta}J(\theta) = \alpha(G_t - V_{\kappa}(s_t)) \nabla_{\theta} \log \pi_{\theta}(s_t,a_t)\)。
TD Difference Actor-Critic策略梯度用TD error来估计，\(\nabla_{\theta}J(\theta) = \alpha \big(r + \gamma V_{\kappa}(s_{t+1}) - V_{\kappa}(s_t) \big) \nabla_{\theta} \log \pi_{\theta}(s_t,a_t)\)。
k-step return Actor-Critic策略梯度用k-step return的误差来估计，\(\nabla_{\theta}J(\theta) = \alpha \big( \sum_{i=0}^k \gamma^i r_{t+i} + \gamma^k V_{\kappa}(s_{t+k}) - V_{\kappa}(s_t) \big) \nabla_{\theta} \log \pi_{\theta}(s_t,a_t)\)。

6.0.5 Summary of PG Algorithms

策略梯度有很多不同形式 \(\begin{aligned} \nabla_{\theta} J(\theta) &=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) G_{t}\right] \text{ ——REINFORCE} \\ &=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) Q^{\mathrm{w}}(s, a)\right] \text{ ——Q Actor-Critic} \\ &=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) A^{\mathrm{w}}(s, a)\right] \text{ ——Advantage Actor-Critic} \\ &=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) \delta\right] \text{ ——TD Actor-Critic} \end{aligned}\)
Critic用策略评估（e.g. MC或TD learning）来估计\(Q^{\pi}(s,a)\)，\(A^{\pi}(s,a)\)或\(V^{\pi}(s)\)。

6.1 Trust Region Policy Optimization

Problems with PG

1. 采样效率低，因为PG是在线学习，\(\nabla_{\theta} J(\theta) = \mathbb{E}_{a \sim \pi_{\theta}} [\nabla_{\theta} \log{ \pi_{\theta}(s,a) r(s,a) }]\)

2. 策略更新过大或步长不当会破坏训练
这点和监督学习不一样，因为在监督学习中学习和数据是独立的。
在RL中，步长过大→坏的策略→坏的数据收集
可能无法从坏的策略中恢复，这会破坏整体的性能

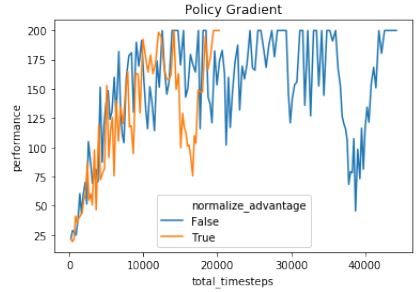
如何使训练更稳定？
— Trust region和natural policy gradient（二阶的优化方式）

如何进行离策略的策略优化？
— 在TRPO中用的重要性采样

6.1.0 Preliminaries

1. Natural policy gradient

策略梯度是欧几里得度量参数空间中最陡的上升：

\[d^{*} = \nabla_{\theta} J(\theta)=\lim _{\epsilon \rightarrow 0} \frac{1}{\epsilon} \arg \max J(\theta+d), \text { s.t. }\|d\| \leq \epsilon\]

它的缺点是对策略函数的参数化很敏感。

以KL-divergence（相对熵）为约束的distribution space（策略输出）中的最陡上升：

\[d^{*} = \arg \max J(\theta+d), \text { s.t. } KL(\pi_{\theta} \| \pi_{\theta+d})=c\]

将KL散度固定为常数\(c\)，可以确保我们以恒定速度沿着分布空间移动，而不管曲率如何（因此对模型参数化具有鲁棒性，因为我们只关心由参数引起的分布）。

KL-divergence as metric for two distributions

KL散度用于度量两个分布的"近似程度"：

\[\color{green}{ KL(\pi_{\theta} \| \pi_{\theta'}) = \mathbb{E}_{\pi_{\theta}}[\log \pi_{\theta}] - \mathbb{E}_{\pi_{\theta}}[\log \pi_{\theta'}] }\]

尽管KL散度是非对称的，因此不是真正的度量，但这不影响我们使用它。这是因为当\(d\)趋向于0时，KL散度是渐进对称的。所以，在局部邻域内KL散度是近似对称的。

我们可以证明KL散度的二阶Taylor展开为

\[KL(\pi_{\theta} \| \pi_{\theta+d}) \approx \frac{1}{2} d^T \mathbf{F} d\]

其中\(\mathbf{F}\)是KL散度的二阶导数\(\mathbb{E}_{\pi_{\theta}} [\nabla \log \pi_{\theta} \nabla \log \pi_{\theta}^T]\)，即Fisher Information Matrix（费舍尔信息矩阵）。

把以KL-divergence（相对熵）为约束的distribution space（策略输出）中的最陡上升\(d^{*} = \arg \max J(\theta+d), \text { s.t. } KL(\pi_{\theta} \| \pi_{\theta+d})=c\)写成Lagrangian形式，\(J(\theta+d)\)由其一阶泰勒展开近似，约束KL散度由其二阶泰勒展开近似，得到

\[\begin{aligned} d^{*} &= \underset{d}{\arg \max } J(\theta+d)-\lambda\left(K L\left(\pi_{\theta} \| \pi_{\theta+d}\right)-c\right) \\ & \approx \underset{d}{\arg \max } J(\theta)+\nabla_{\theta} J(\theta)^{T} d-\frac{1}{2} \lambda d^{T} F d+\lambda c \end{aligned}\]

为了求最大化，我们令其关于\(d\)的导数为零，得到natural Policy gradient \(d = \frac{1}{\lambda} \mathbf{F}^{-1} \nabla_{\theta} J(\theta)\)。

自然策略梯度是二阶优化，更加准确而且与模型如何参数化无关（model invariant）。

\[\theta_{t+1} = \theta_t + \alpha \mathbf{F}^{-1} \nabla_{\theta} J(\theta)\]

其中，\(\mathbf{F} = \mathbb{E}_{\pi_{\theta}(s,a)} [\nabla \log \pi_{\theta}(s,a) \nabla \log \pi_{\theta}(s,a)^T]\)为Fisher信息矩阵，即KL散度的二阶微分。\(\mathbf{F}\)度量了策略（分布）关于模型参数\(\theta\)的曲率。

补充

无论模型如何参数化，自然策略梯度都会产生相同的策略变化。

关于自然梯度：A Natural Policy Gradient, 2001、techblog: Natural Gradient Descent、知乎：自然策略梯度。

2. PG with IS

我们可以利用重要性采样将策略梯度变成离策略学习。重要性采样（important sampling, IS）：计算\(f(x)\)的期望值，其中\(x\)具有数据分布\(p\)。我们可以从另一个分布\(q\)中采样数据，使用\(p\)和\(q\)之间的概率比重新校准结果。（IS代码示例）

\[\mathbb{E}_{x \sim p} [f(x)] = \int p(x)f(x)dx = \int q(x) \frac{p(x)}{q(x)} dx = \mathbb{E}_{x \sim q} \left[ \frac{p(x)}{q(x)} f(x) \right]\]

对策略目标进行重要性采样

\[J(\theta) = \mathbb{E}_{\color{green}{a \sim \pi_{\theta}}} \color{black}{[r(s,a)]} = \mathbb{E}_{\color{green}{a \sim \hat{\pi}}} \color{black}{\left[ \frac{\pi_{\theta}(s,a)}{\hat{\pi}(s,a)} r(s,a) \right]}\]

6.1.1 Increasing the robustness with TR

行为策略可以直接是旧策略，因此我们可以有一个替代目标函数

\[\theta = \underset{\theta}{\arg \max } J_{\theta_{\text {old }}}(\theta) = \underset{\theta}{\arg \max } \mathbb{E}_{t}\left[\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)} R_{t}\right]\]

当\(\pi_{\theta} / \pi_{\theta_{\text{old}}}\)太大时，估计值可能会过大。解决方案：限制后续策略之间的差异。比如，用KL散度来测量两个策略之间的距离

\[KL(\pi_{\theta_{\text{old}}} \| \pi_{\theta}) = - \sum_a \pi_{\theta_{\text{old}}}(a \vert s) \log \frac{\pi_{\theta}(a \vert s)}{\pi_{\theta_{\text{old}}}(a \vert s)}\]

因此，包含置信区间的目标变成最大化

\[\begin{aligned} & J_{\theta_{\text {old }}}(\theta) = \mathbb{E}_t \left[\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{\text {old }}}\left(a_t \mid s_t\right)} R_t\right] \\ & \text {s.t. } KL \big(\pi_{\theta_{\text {old }}} \left(. \mid s_t\right) \| \pi_\theta \left(. \mid s_t\right)\big) \leq \delta \end{aligned}\]

在置信区间中，我们将参数搜索限制在一个由\(\delta\)控制的区域内。这是TRPO和PPO背后的思想。

6.1.2 Trust region optimization

将用Taylor展开到二阶，经推导可得

\[\begin{aligned} J_{\theta_t}(\theta) & \approx g^T (\theta-\theta_t) \\ K L\left(\theta_t \| \theta\right) & \approx \frac{1}{2} (\theta-\theta_t)^T H (\theta-\theta_t) \end{aligned}\]

其中，\(g = \nabla_{\theta} J_{\theta_t}(\theta)\)，\(H = \nabla_{\theta}^2 KL(\theta_t \| \theta)\)，\(\theta_t\)即\(\theta_{\text{old}}\)。

那么目标变为：

\[\begin{aligned} & \theta_{t+1} = \operatorname{arg max}_{\theta} g^T(\theta-\theta_t) \\ & \text{s.t. } \frac{1}{2} (\theta-\theta_t)^T H (\theta-\theta_t) \le \delta \end{aligned}\]

这是一个二次方程，可以求解析解：

\[\theta_{t+1} = \theta_t + \sqrt{\frac{2 \delta}{g^T H^{-1} g}} H^{-1} g\]

补充

TRPO的参数更新中没有设置步长，这里我们认为步长是跟δ的大小相关（即上式中的根号项）。所以在TRPO中只需要给出我们希望新策略和旧策略间相距多少即可。

6.1.3 Natural policy gradient

自然梯度是相对于Fisher信息的最陡上升方向，\(H\)即为Fisher信息矩阵（FIM），其计算如下

\[H =\nabla_\theta^2 K L\left(\pi_{\theta_t} \| \pi_\theta\right)=E_{a, s \sim \pi_{\theta_t}}\left[\nabla_\theta \log \pi_\theta(a, s) \nabla_\theta \log \pi_\theta(a, s)^T\right]\]

学习率 (\(\delta\)) 可以被认为是选择了一个根据策略变化标准化的步长。这是有益的，因为这意味着任何参数更新都不会显著改变策略网络的输出。

6.1.4 TRPO

FIM及其转置计算成本很高，所以TRPO通过解线性方程\(H \mathbf{x} = g\)来估计\(\mathbf{x} = H^{-1} g\)。

考虑二次方程的优化。解\(\mathbf{Ax = b}\)等价于\(\mathbf{x} = \operatorname{arg max}_{\mathbf{x}} \frac{1}{2} \mathbf{x}^T \mathbf{Ax} - \mathbf{b}^T \mathbf{x}\)，由于\(f'(\mathbf{x}) = \mathbf{Ax - b} = 0\)，所以我们可以把二次方程优化为

\[\min_{\mathbf{x}} \frac{1}{2} \mathbf{x}^T H \mathbf{x} - g^T \mathbf{x}\]

用共轭梯度法求解。它与梯度上升非常相似，但可以在较少的迭代中完成。

TRPO论文的附录A提供了一个2页证明，证明此方法可保证单调改进，即每次TRPO迭代中的策略更新都会创建更好的策略

\[J(\pi_{t+1}) - J(\pi_t) \ge M_t(\pi_{t+1}) - M(\pi_t) \qquad \text{where } M_t(\pi) = L_{\pi_t}(\pi)-\alpha D_{KL}(\pi_t, \pi)\]

因此，通过在每次迭代时最大化\(M_t\)，可以保证真实目标\(J\)是不会减小的。它是一种Minorize-Maximization (MM) 算法，是一类包含期望最大化的方法。MM算法通过最大化代理函数（下面的蓝线）来迭代地实现这一点，该代理函数近似于本地的预期回报。

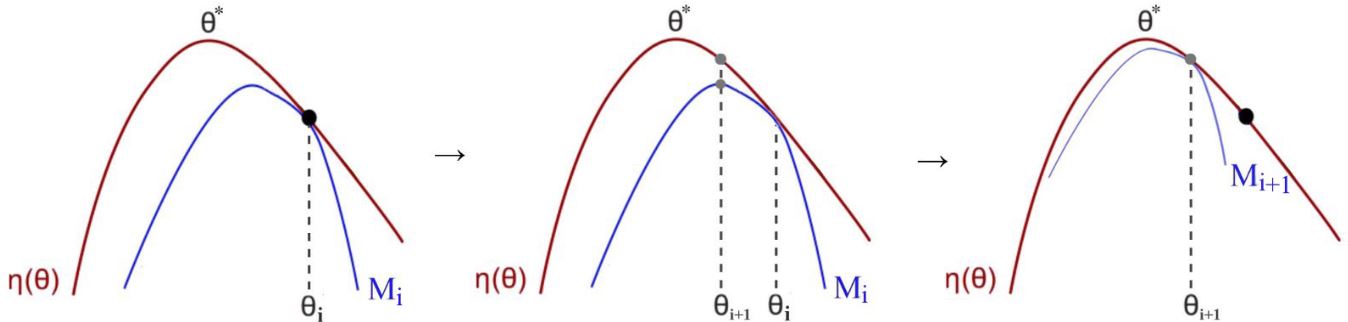
Result & Demo of TRPO

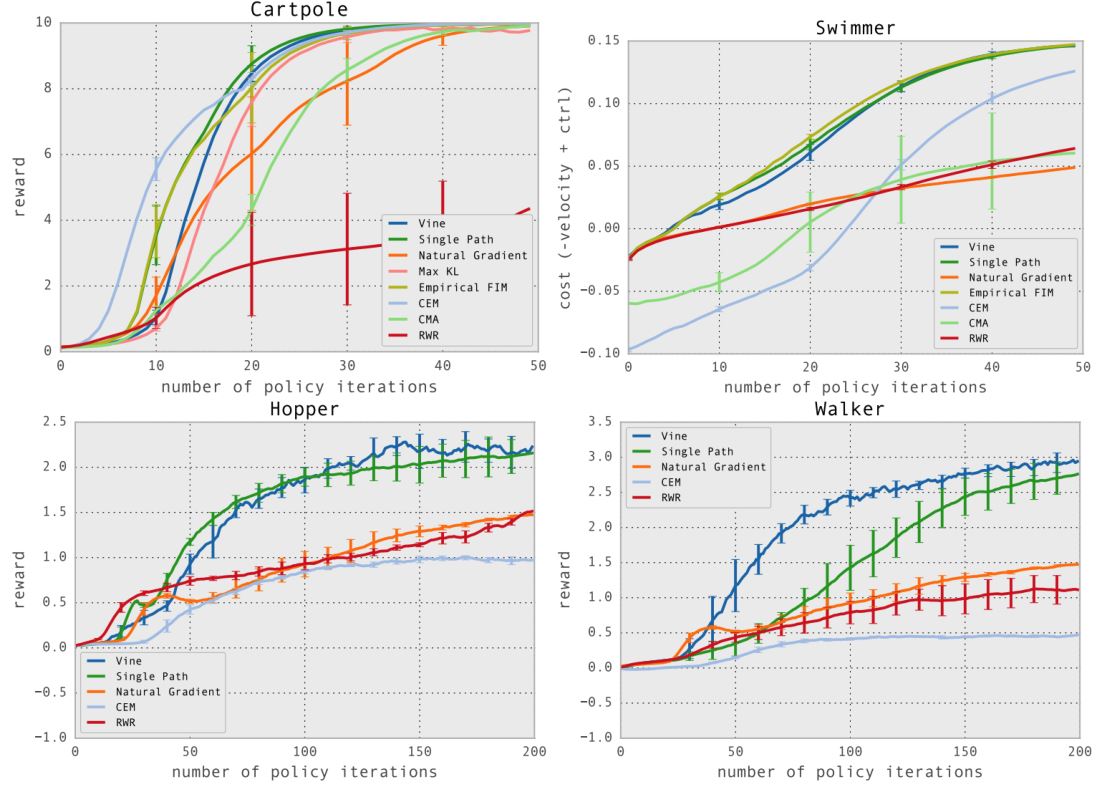
演示视频位于(https://www.youtube.com/watch?v=KJ15iGGJFvQ)。

6.1.5 Limitations of TRPO

TRPO的可扩展性问题
每次为当前策略模型计算\(H\)代价很高
需要大量rollout才能逼近\(H\)， \(H=E_{s, a \sim \pi_{\theta_t}}\left[\left(\nabla_\theta \log \pi_\theta(s, a)\right)^T\left(\nabla_\theta \log \pi_\theta(s, a)\right)\right]\)
共轭梯度（Conjugate Gradient, CG）使实现更加复杂
TRPO在有些任务的表现上不如DQN

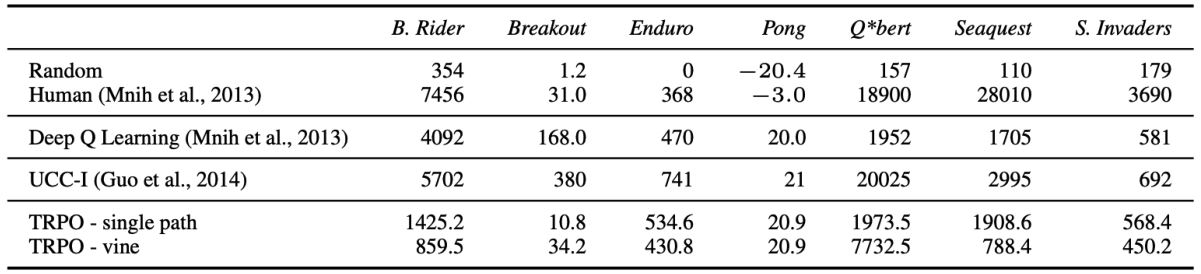
6.2 ACKTR: Calculate Natural Gradient with K-FAC

ACKTR用Kronecker因子近似曲率（K-FAC）简化了Fisher信息矩阵（FIM）的求逆过程，加速了优化。

\[\mathbf{F} = \mathbb{E}_{x \sim \pi_{\theta_t}} \big[ \big( \nabla_\theta \log \pi_\theta(x) \big)^T \big( \nabla_\theta \log \pi_\theta(x) \big) \big]\]

替换为逐层计算

\[\color{green}{\begin{aligned} F_{\ell} &= \mathbb{E}[\operatorname{vec} \{\nabla_W L\} \operatorname{vec}\{\nabla_W L\}^T] = \mathbb{E}[a a^T \otimes \nabla_s L (\nabla_s L)^T] \\ & \approx \mathbb{E}[a a^T] \otimes \mathbb{E}[\nabla_s L (\nabla_s L)^T] := A \otimes S :=\hat{F}_{\ell} \end{aligned}}\]

其中，\(A\)表示\(\mathbb{E}[a a^T]\)，\(S\)表示\(\mathbb{E}[\nabla_s L (\nabla_s L)^T]\)。

随机梯度下降（SGD）是一阶优化，广泛用于网络优化；自然梯度下降在迭代方面比一阶方法收敛更快，因为考虑了损失函数的曲率，尽管它需要计算Fisher信息矩阵 \(\theta_{t+1} = \theta_t + \alpha \mathbf{F}^{-1} \nabla_\theta J(\theta)\)，其中\(\mathbf{F} = \mathbb{E}_{\pi_\theta(s, a)} [\nabla \log \pi_\theta(s, a) \nabla \log \pi_\theta(s, a)^T ]\)。K-FAC用于大规模神经网络优化的FIM估计。

补充

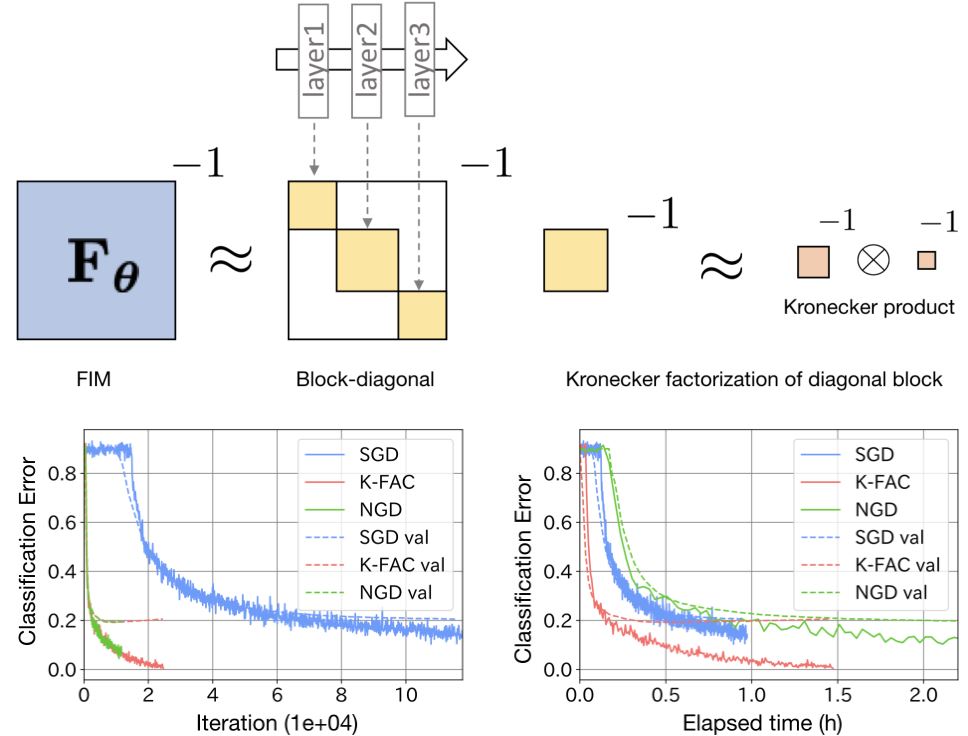
神经网络的FIM是分块对角矩阵，因为每层只和层内的系数相关，所以可以用K-FAC来加速FIM的求逆。

Performance of ACKTR

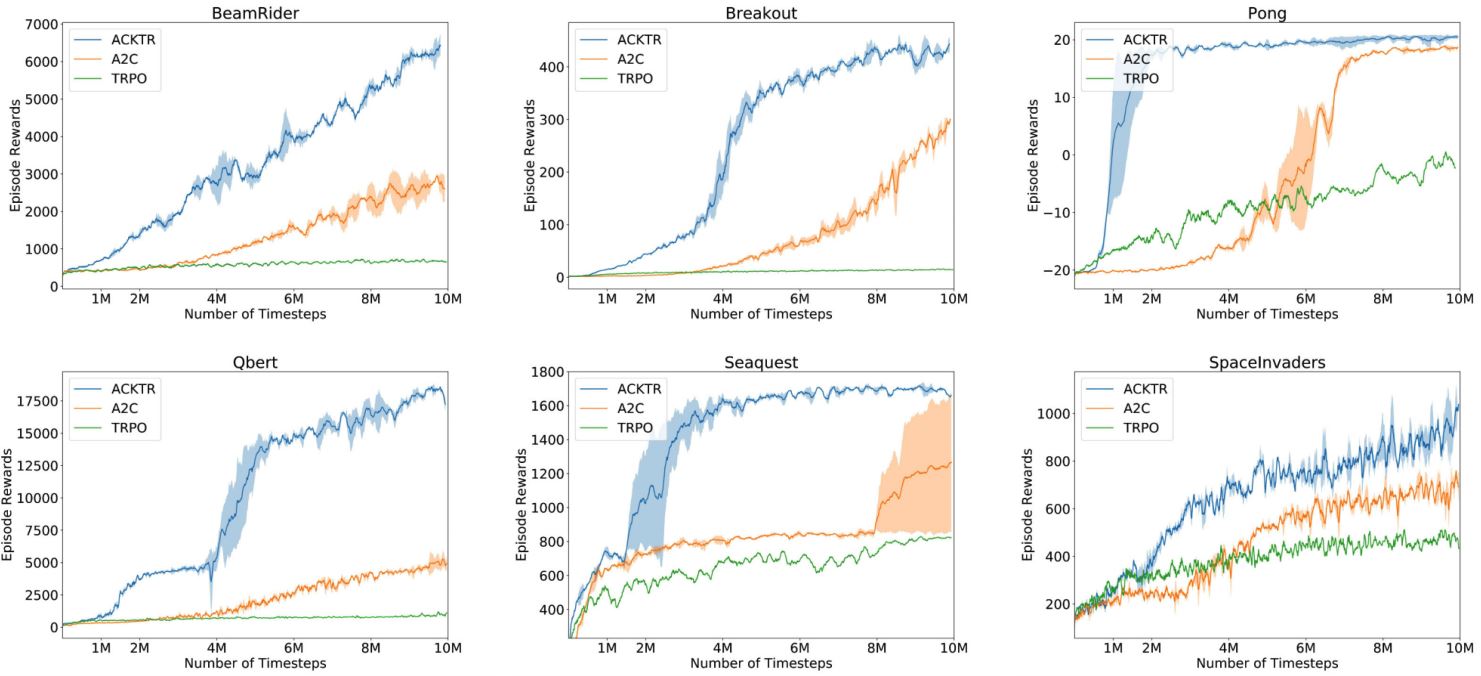
介绍链接：OpenAI: ACKTR & A2C

6.3 Proximal Policy Optimization

6.3.1 PPO

自然梯度和TRPO中的损失函数

\[\begin{aligned} \max_\theta \quad & \mathbb{E}_t \left[\frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{\text {old }}}(a_t \mid s_t)} A_t\right] \\ \text {s.t.} \quad & \mathbb{E}_t \big[ K L[\pi_{\theta_{\text{old}}}(. \mid s_t), \pi_\theta(. \mid s_t)] \big] \leq \delta \end{aligned}\]

也可以写成无约束的形式

\[\color{green}{ \max_\theta \mathbb{E}_t \left[\frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{\text {old }}}(a_t \mid s_t)} A_t\right] - \beta \mathbb{E}_t \big[ K L[\pi_{\theta_{\text{old}}}(. \mid s_t), \pi_\theta(. \mid s_t)] \big] }\]

PPO：引入自适应的KL惩罚，所以能更好地保证在置信区域内进行优化。性能与TRPO相当，但是因为用一阶优化（SGD）所以求解速度快很多。

6.3.2 PPO with clipping

用\(r_t(\theta)\)表示概率比\(r_t(\theta) = \frac{\pi_\theta(a_t \vert s_t)}{\pi_{\theta_{\text{old}}}(a_t \vert s_t)}\)，所以不同的替代目标有：
1. PG（无置信域）：\(L_t(\theta) = r_t(\theta) \hat{A}_t\)
2. KL约束：\(L_t(\theta) = r_t(\theta) \hat{A}_t ,\ \text{s.t. } KL[\pi_{\theta_{\text{old}}}, \pi_\theta] \le \delta\)
3. KL惩罚：\(L_t(\theta) = r_t(\theta) \hat{A}_t - \beta KL[\pi_{\theta_{\text{old}}}, \pi_\theta]\)

如果新策略与旧策略距离很远（r_t很大），就用一个新的目标函数来截断估计的advantage函数

\[\color{green}{ L_t(\theta) = \min \left(r_t(\theta) \hat{A}_t, \operatorname{clip}\left(r_t(\theta), 1-\epsilon, 1+\epsilon\right) \hat{A}_t\right) }\]

如果新旧策略的概率比在\(1-\epsilon ,\ 1+\epsilon\)的范围之外，那么advantage函数会被截断。（在PPO论文中，\(\epsilon\)被设为2。）

Clipping的作用类似于一个正则化器，消除了激励策略发生巨大变化的因素。当advantage为正时，我们鼓励动作，因此\(\pi_\theta(a \vert s)\)变大，

\[L\left(\theta ; \theta_{\text{old}}\right) = \min \left( \frac{\pi_\theta(a_t \vert s_t)}{\pi_{\theta_{\text{old}}}(a_t \vert s_t)}, (1 + \epsilon) \right) \hat{A}_t\]

当advantage为负时，我们不鼓励动作，因此\(\pi_\theta(a \vert s)\)变小，

\[L\left(\theta ; \theta_{\text{old}}\right) = \max \left( \frac{\pi_\theta(a_t \vert s_t)}{\pi_{\theta_{\text{old}}}(a_t \vert s_t)}, (1 - \epsilon) \right) \hat{A}_t\]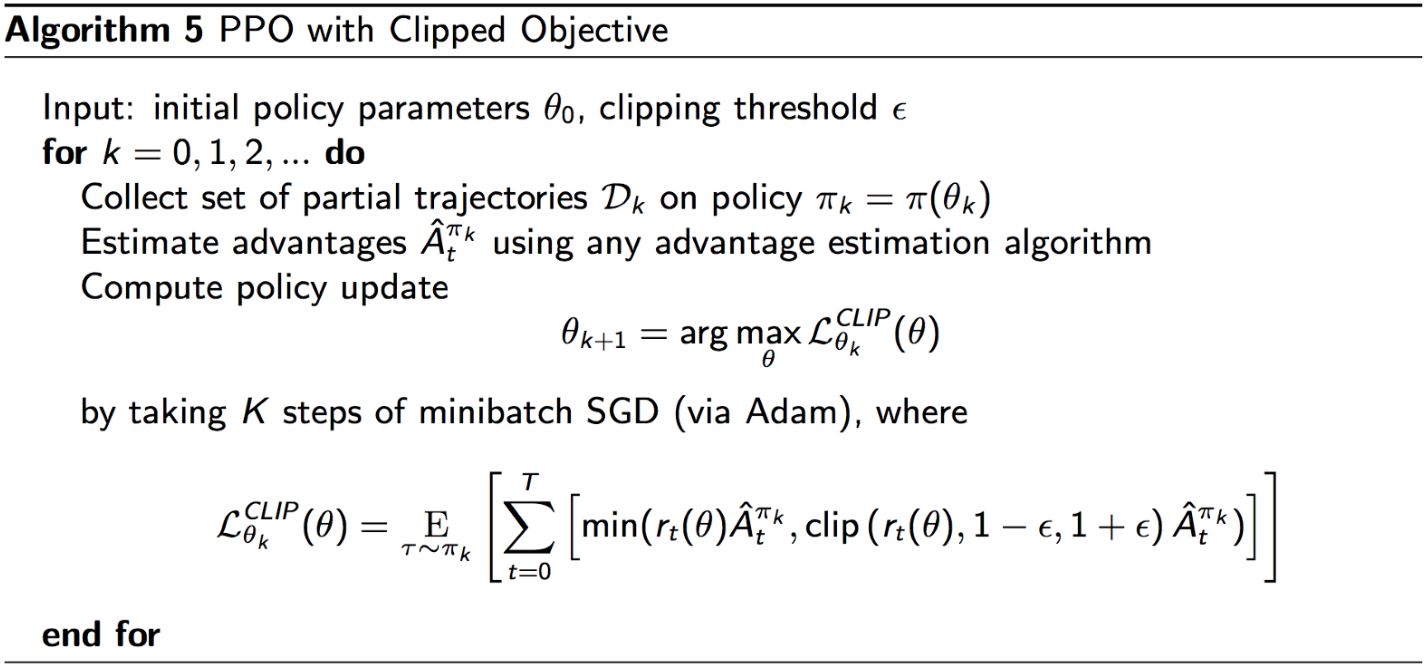

PPO有置信域方法的稳定性和可靠性，实现上却简单很多，只需在原始策略梯度的基础上改几行代码即可实现。

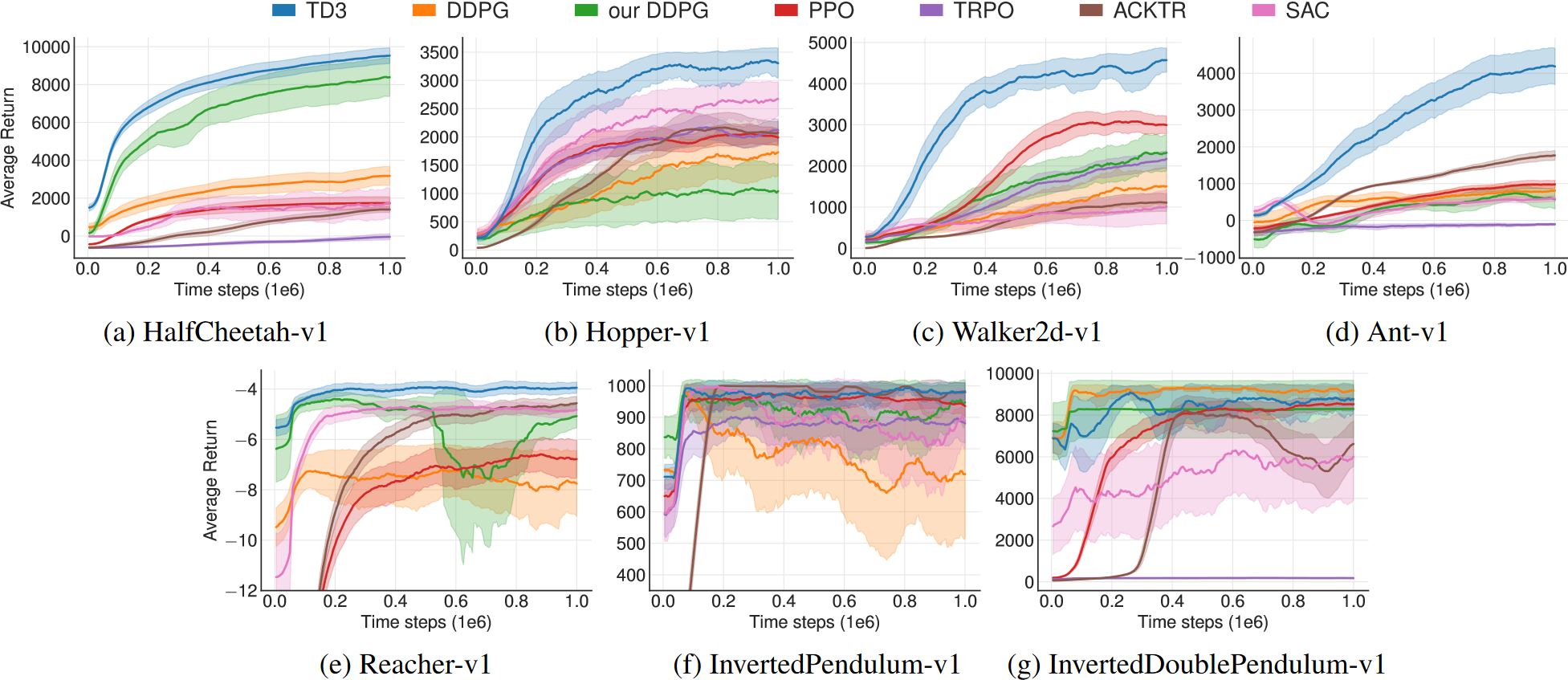
Result of PPO

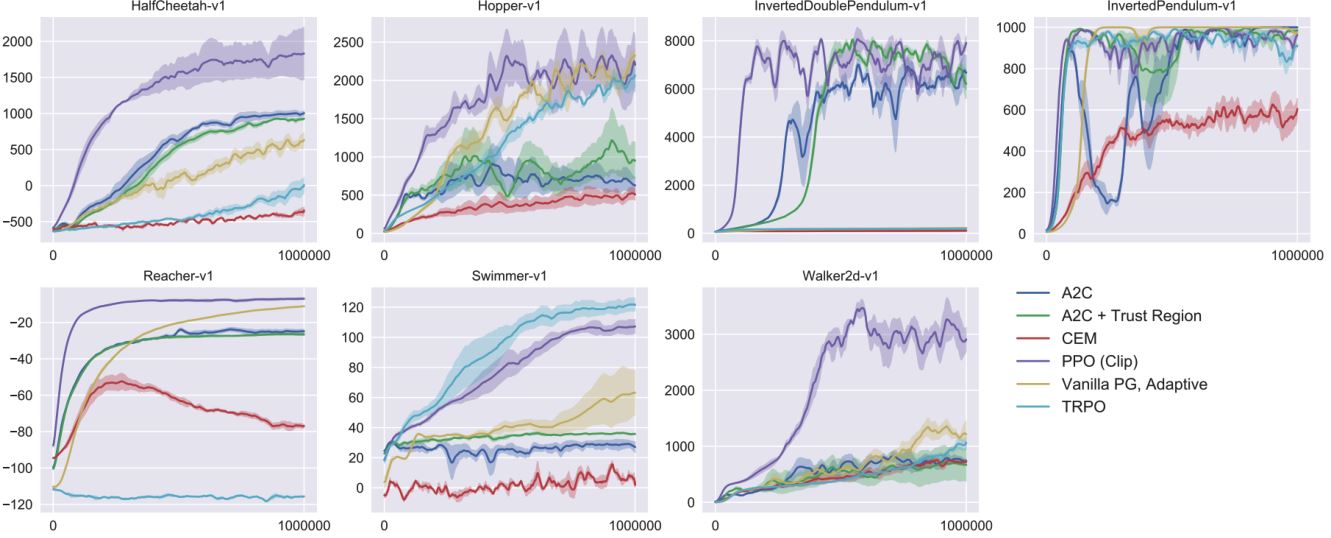
Result on the continuous control tasks (MuJuCo)

Demo of PPO (by OpenAI)
复杂环境下运动行为的出现分布式PPO (by DeepMind)
Code example

补充

目前SOTA的强化学习方法大多是基于策略的。

TRPO：具有可靠的数学证明和保证，但难以遵循
ACKTR：基于数值优化的改进，可扩展到实际问题
PPO：可读性好，损失函数设计优雅，易于实现，广泛使用

6.4 Deep Deterministic Policy Gradient

动机：如何将DQN拓展道连续动作空间的环境中？

DDPG与DQN十分相似，可以看作是DQN的连续动作空间版

\[\begin{aligned} \text{DQN: } & a^* =\underset{a}{\arg \max } Q^*(s, a) \\ \text{DDPG: } & a^* =\underset{a}{\arg \max } Q^*(s, a) \approx Q_\phi(s, \mu_\theta(s)) \end{aligned}\]

可以看出，DDPG中确定性策略\(\mu_\theta(s)\)直接给出了最大化\(Q_\phi(s, a)\)的动作。由于动作\(a\)是连续的，所以我们假设Q-函数\(Q_\phi(s, a)\)关于\(a\)是可微的。

因此，DDPG有如下目标：

\[\begin{aligned} \text{Q-target: } & y(r, s^{\prime}, d) = r + \gamma(1-d) Q_{\phi_{targ}}(s^{\prime}, \mu_{\theta_{targ}}(s^{\prime})) \\ \text{Q-function: } & \min \mathbb{E}_{s, r, s^{\prime}, d \sim \mathcal{D}}[Q_\phi(s, a) - y(r, s^{\prime}, d)] \\ \text{policy: } & \max_\theta \mathbb{E}_{s \sim \mathcal{D}}[Q_\phi(s, \mu_\theta(s))] \end{aligned}\]

对价值和策略网络应用经验回放及目标网络的trick是和DQN里一样的。DDPG的示例代码（采用与TD3一样的样本代码库）

6.5 Twin Delayed DDPG (TD3)

DDPG的一个主要缺点就是学到的\(Q\)函数有时会显著地高估\(Q\)值，导致策略崩盘。真实价值是通过沿当前策略执行1000个episode以上的平均折扣return得来的。

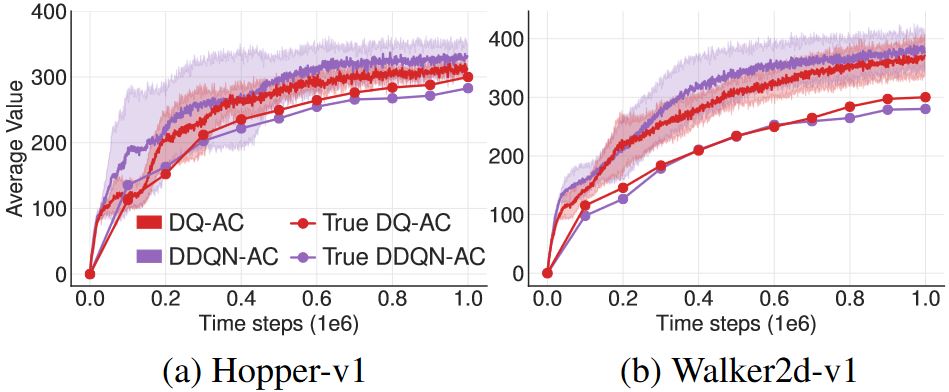
在MuJoCo环境下，Double DQN和Double Q-learning的不同actor-critic变体对价值估计的overestimate偏差对比

TD3提出了三点改进（tricks？）

Clipped Double-Q Learning. TD3学习两个\(Q\)函数而不是一个（"twin"的含义），并用两个\(Q\)值中较小的那个生成Bellman误差损失函数中的目标。
"Delayed" Policy Updates. TD3以比\(Q\)函数更新频率更低的频率更新策略（和目标网络）。原文推荐每两次\(Q\)函数更新对应一次策略更新。
Target Policy Smoothing. TD3在目标动作中加入噪声，使得策略更难通过沿着动作的变化平滑\(Q\)来利用\(Q\)函数误差。

TD3同时学习两个\(Q\)函数，\(Q_{\phi_1}\)和\(Q_{\phi_2}\)，通过最小化均方Bellman误差。两个\(Q\)函数都用同一个目标，使用两个\(Q\)函数给出的较小的那个值作为后续的\(Q\)-target：

\[y(r, s^{\prime}, d) = r + \gamma(1-d) \min _{i=1,2} Q_{\phi_{i, targ}}(s^{\prime}, \color{green}{a_{TD3}(s^{\prime})} \color{balck}{)}\]

目标策略平滑如下：

\[\color{green}{a_{TD3}(s^{\prime})} = \color{black}{ \operatorname{clip} \left( \mu_{\theta, \operatorname{targ}}(s^{\prime}) + \operatorname{clip}(\epsilon,-c, c), a_{low}, a_{high} \right), \epsilon \sim \mathcal{N}(0, \sigma) }\]

这步的作用和正则化一样：防止策略的动作输出包含错误的尖峰。

作者的Pytorch实现（非常简洁的实现！）这个仓库下还有DDPG与TD3不同之处的对比。

6.6 Soft Actor-Critic (SAC)

SAC以离策略的方式优化了一个随机策略，统一了随机策略优化和DDPG风格的方法。SAC引入了entropy regularization，熵是描述一个随机变量的随机程度的量，\(H(P) = \mathbb{E}_{x \sim P}[- \log P(x)]\)。

Entropy-regularized RL：策略被训练来最大化期望return和熵之间的平衡。

\[\color{green}{ \pi^* = \arg \max \mathbb{E}_{\tau \sim \pi} \left[ \sum_t \gamma^t (R(s_t, a_t, s_{t+1}) + \alpha H(\pi(. \mid s_t))) \right] }\]

价值函数中加入每个时间的熵

\[V^\pi(s) = \mathbb{E}_{\tau \sim \pi} \left[ \sum_t \gamma^t(R(s_t, a_t, s_{t+1}) + \alpha H(\pi(. \mid s_t))) \mid s_0 = s \right]\]

熵归一化的\(Q^\pi\)的Bellman递归方程

\[\begin{aligned} Q^\pi(s, a) &= \mathbb{E}_{s^{\prime} \sim P, a^{\prime} \sim \pi} [R(s, a, s^{\prime}) + \gamma(Q^\pi(s^{\prime}, a^{\prime}) + \alpha H(\pi(. \mid s^{\prime})))] \\ &= \mathbb{E}_{s^{\prime} \sim P, a^{\prime} \sim \pi} [R(s, a, s^{\prime}) + \gamma(Q^\pi(s^{\prime}, a^{\prime}) - \alpha \log \pi(a^{\prime} \mid s^{\prime}))] \end{aligned}\]

所以，Q函数的采样更新为

\[Q^\pi(s, a) \approx r + \gamma (Q^\pi(s^{\prime}, \hat{a}^{\prime}) - \alpha \log \pi(\hat{a}^{\prime} \mid s^{\prime})),\ \hat{a}^{\prime} \sim \pi(. \mid s^{\prime})\]

SAC同时学习一个策略\(\pi_\theta\)和两个Q函数\(Q_{\phi_1}\)、\(Q_{\phi_1}\)。和TD3一样，共用的目标中使用了clipped Double-Q trick，两个Q函数都是通过最小化Bellman均方差的方式来学习的。

\[\begin{aligned} L(\phi_i, \mathcal{D}) &= \mathbb{E}[(Q_\phi(s, a) - y(r, s^{\prime}, d)^2] \\ y(r, s^{\prime}, d) &= r + \gamma (1-d) \left( \min _{j=1,2} Q_{\phi_{\text{targ}, j}}(s^{\prime}, \hat{a}^{\prime}) - \alpha \log \pi(\hat{a}^{\prime} \mid s^{\prime}) \right),\ \hat{a}^{\prime} \sim \pi_\theta(. \mid s^{\prime}) \end{aligned}\]

策略是通过最大化期望未来return与期望未来熵的和来学习的，因此最大化

\[\begin{aligned} V^\pi(s) &= \mathbb{E}_{a \sim \pi}[Q^\pi(s, a) + \alpha H(\pi(. \mid s))] \\ &= \mathbb{E}_{a \sim \pi}[Q^\pi(s, a) - \alpha \log \pi(a \mid s)] \end{aligned}\]