Introduction

  本课程将聚集深度学习，如果说机器学习=寻找函数，那么深度学习中机器就是要找一个函数，而这个函数是一个类神经网络。函数的输入可以有很多种类，向量、矩阵、序列等。

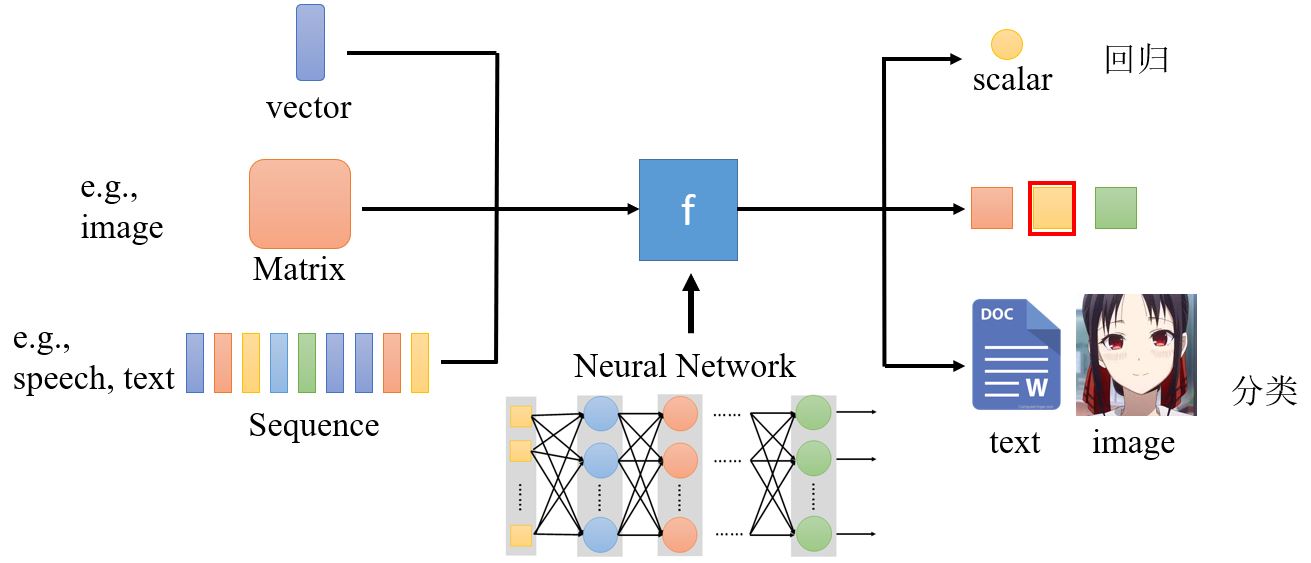
机器学习的框架：

1. Function with unknown parameters

\[y = f(\qquad) \rightarrow y = b + w x_1\]

  根据domain knowledge将\(y = f(\quad)\)写出model \(y = b + w x_1\)，其中，\(y\)和\(x_1\)为feature，\(w\)和\(b\)为未知参数，称\(w\)为weight，称\(b\)为bias。

2. Define loss from training data

  Loss是关于参数的函数\(L(b,w)\)，用于评估一组值的好坏程度。

令loss：\(L = \frac{1}{N} \sum_n e_n\)
  若\(e = \| y - \hat{y} \|\)，则\(L\)为mean absolute error (MAE)
  若\(e = (y - \hat{y})^2\)，则\(L\)为mean square error (MSE)。

如果\(y\)和\(\hat{y}\)都是概率分布，可以选择cross entropy（交叉熵）作为loss。

3. Optimization

Gradient descent \(w^*, b^* = \arg \min_{w, b} L\)

  • （随机）选取一个初始值\(w^0\)，\(b^0\)
  • 计算\(\frac{\partial L}{\partial w} \vert_{w = w_0, b = b_0}\)和\(\frac{\partial L}{\partial b} \vert_{w = w_0, b = b_0}\)
    通过选取合适的learning rate \(\color{green}{\eta}\)来控制更新的步长。因为\(\eta\)是人为选定的，所以是一个hyperparameter。
      \(w^1 \leftarrow w^0 - \eta \frac{\partial L}{\partial w} \vert_{w = w_0, b = b_0} \qquad b^1 \leftarrow b^0 - \eta \frac{\partial L}{\partial b} \vert_{w = w_0, b = b_0}\)
  • 迭代更新\(w\)和\(b\)
注意

梯度下降法可能会陷入局部极值，但这并不是在这个方法中所要解决的真正难题。

1.1 Function with unknown

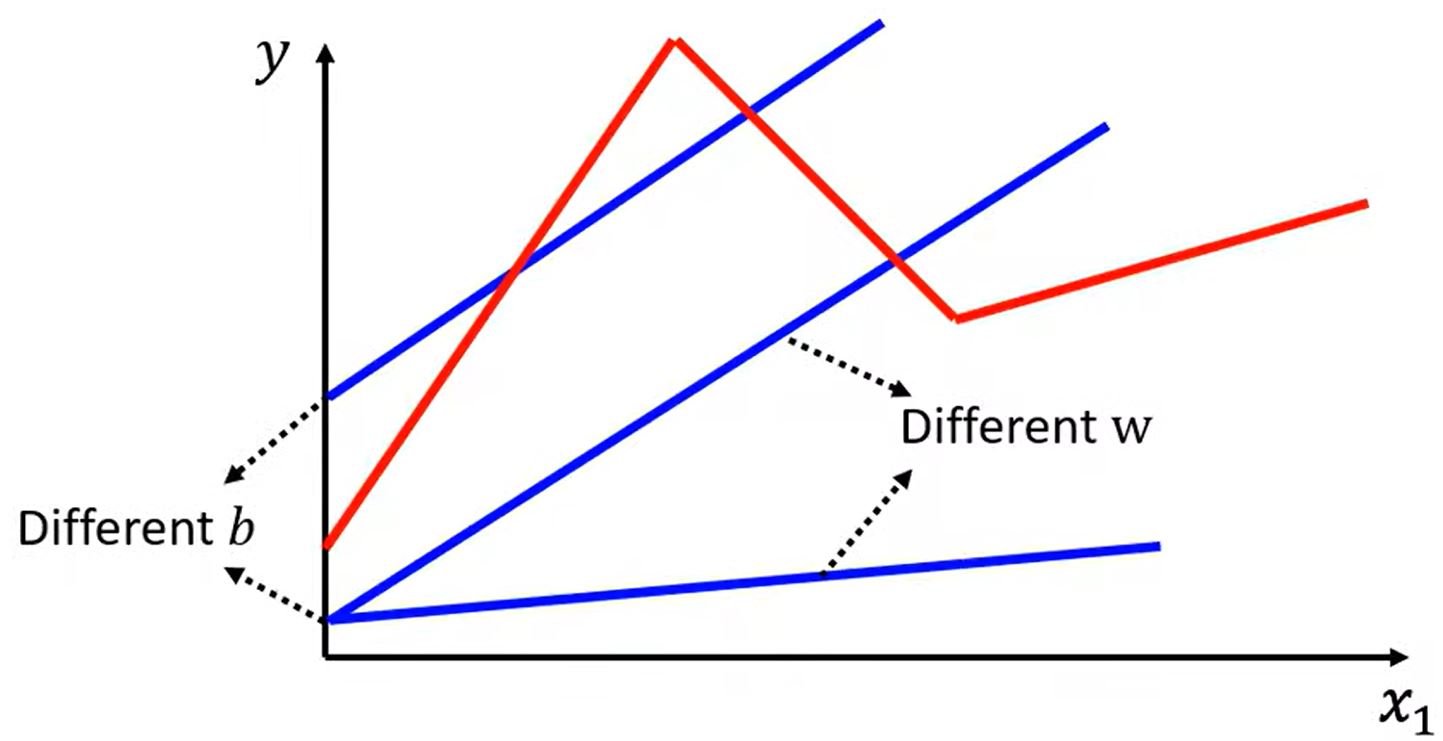
  前面我们考虑了线性模型\(y = b + w x_1\)，但是线性模型非常受限，即有model bias，所以还需要更加复杂的模型。

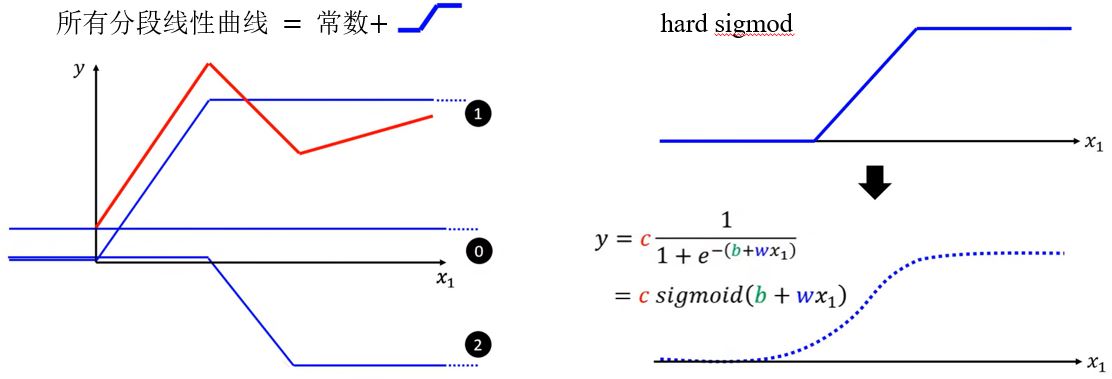
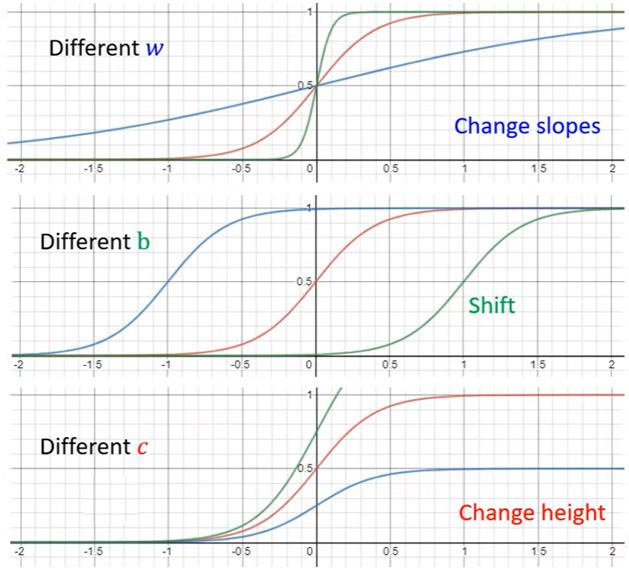
  所有的分段线性曲线可以用常数和如下图所示的蓝色曲线组成，而所有连续曲线都可以用分段线性曲线来近似。这个蓝色曲线可以用sigmod函数\(\color{green}{y =c \frac{1}{1+e^{-(b+w x_1)}} = c \operatorname{sigmoid}(b+w x_{1})}\)来近似。通过改变\(w\)、\(b\)和\(c\)可以得到不同形状的sigmod函数。

这样，就可以得到新的模型（更多特征）：

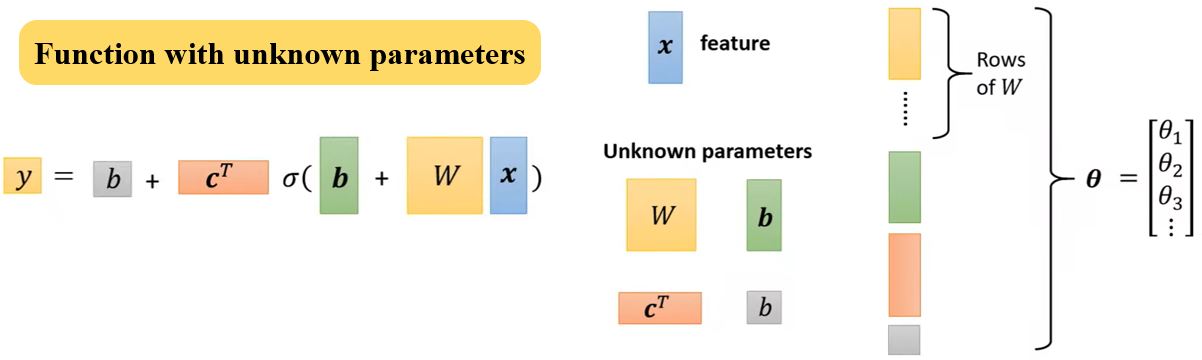
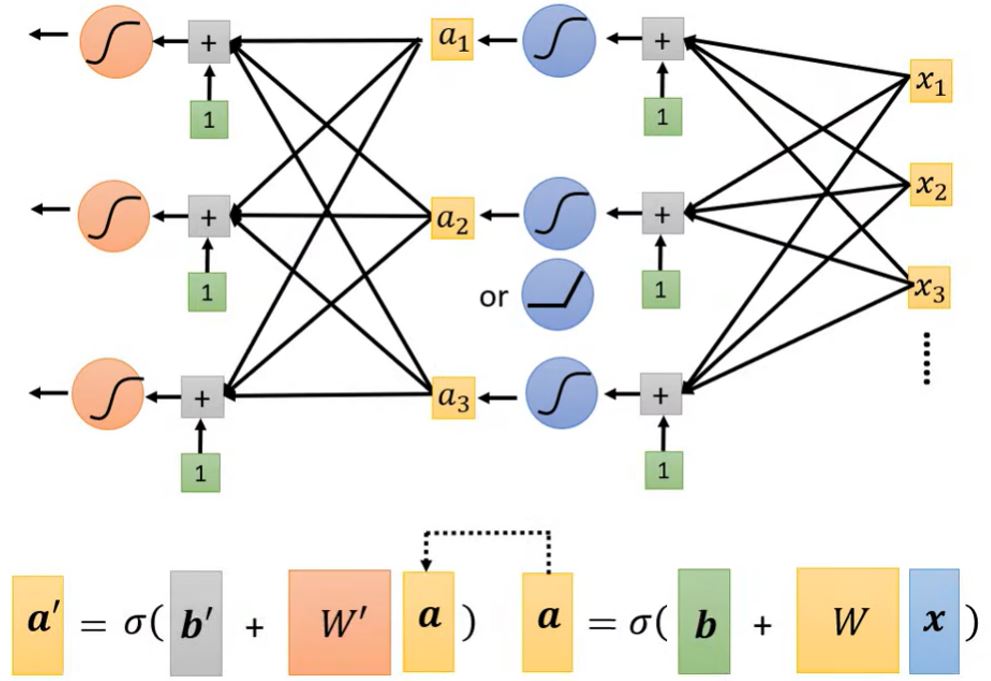
\[y = b + w x_1 \rightarrow y = b + \sum_i c_i \operatorname{sigmoid}(b_i + w_i x_1)\] \[y = b + \sum_j w_j x_j \rightarrow \boxed{y = b + \sum_i c_i \operatorname{sigmoid}(b_i + \sum_j w_{ij} x_j)}\]

其中，\(j\)是特征的序号，\(i\)是sigmoid的序号。

  下面，以\(i = 1, 2, 3\)和\(j = 1, 2, 3\)的情况为例。

提示

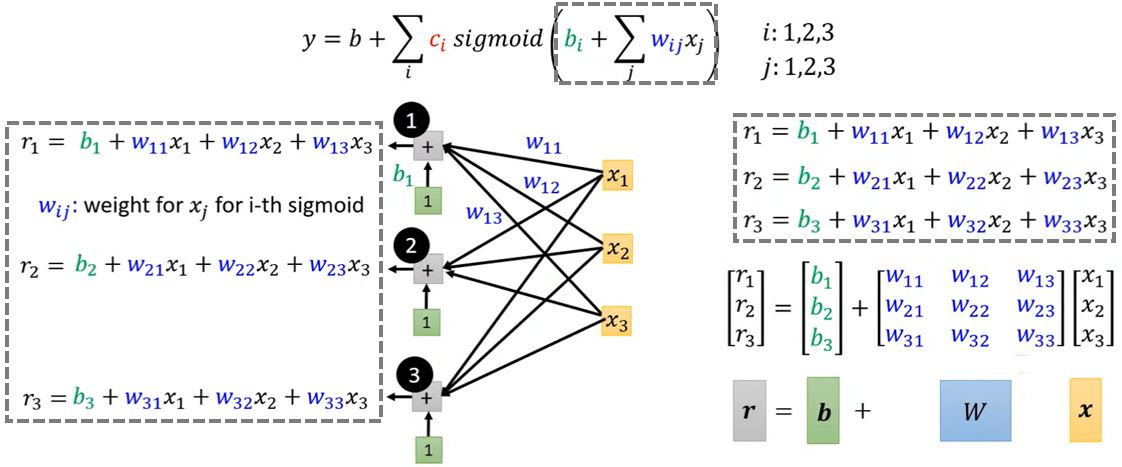
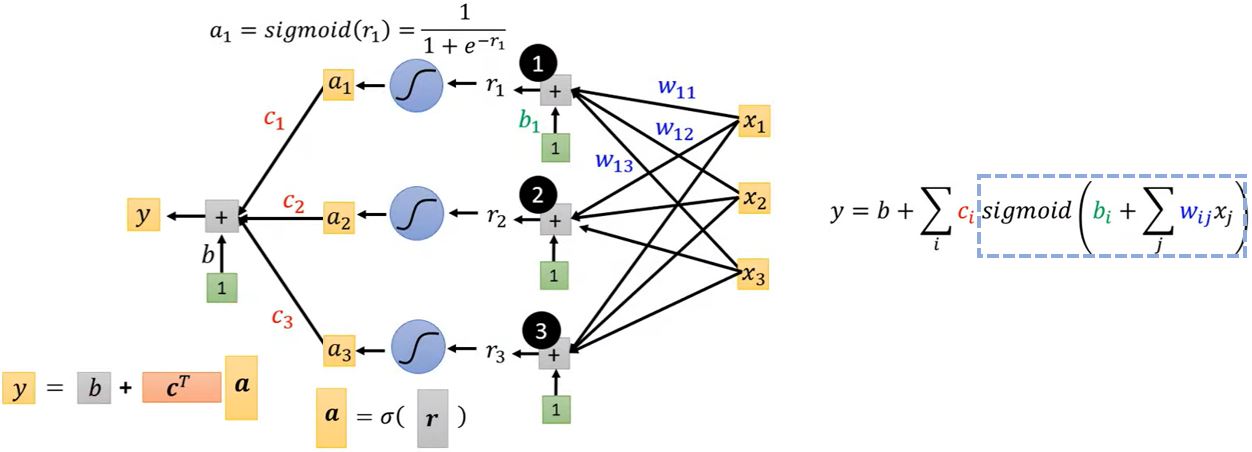
这里出现的神经网络模型是在1943年由心理学家W. S. McCulloch和数理逻辑学家W. Pitts提出的MP（McCulloch-Pitts）模型，该模型将外部输入模拟成一串数字，将每个树突对输入刺激的加工过程模拟为以某个权重对输入进行加权求和，将细胞核对输入的处理模拟为一个带有偏置的加权求和，最后的输出是用激活函数对求和的结果进行非线性变换得出。虽然这个模型并不能反应真实的神经元运作机制，但是这个模型在机器学习领域应用很广泛。

1.2 Define Loss

  Loss是关于参数的函数\(L(b,w)\)，用于评估一组值的好坏程度。

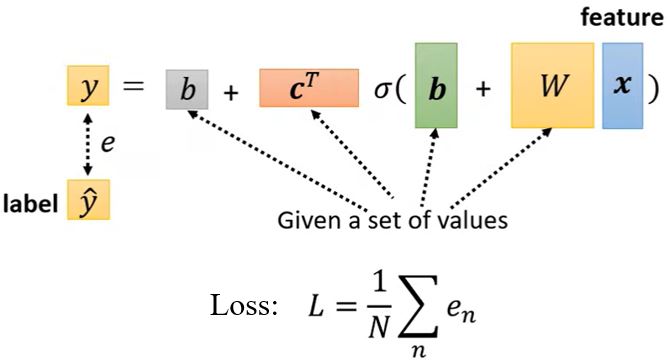
1.3 Optimization

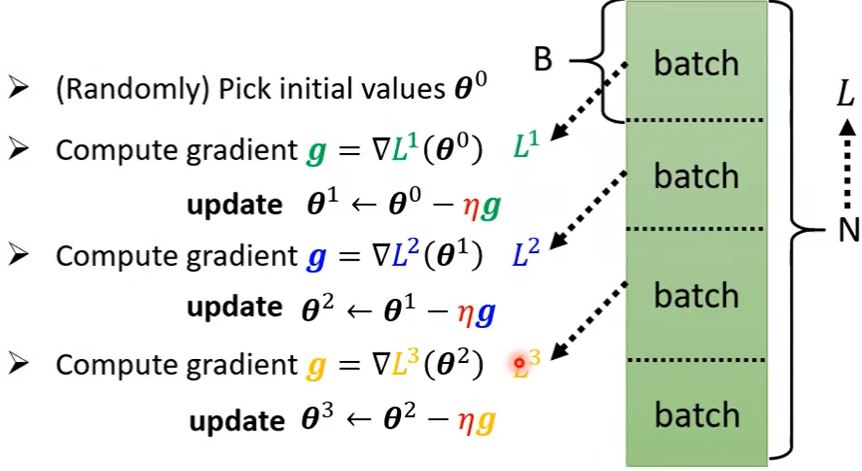
\[\pmb{\theta}^* = \arg \min_{\theta} L \qquad \pmb{\theta} = \begin{bmatrix} \theta_1 \\ \theta_2 \\ \theta_3 \\ \vdots \end{bmatrix}\]
  • （随机）选择初始值\(\pmb{\theta}^0\)
  • 计算梯度\(\boldsymbol{g}=\nabla L(\pmb{\theta}^0)\)，\(\pmb{\theta}^1 \leftarrow \pmb{\theta}^0 - \eta \boldsymbol{g}\)
      \(\boldsymbol{g}=\begin{bmatrix}\left.\frac{\partial L}{\partial \theta_{1}}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}^{0}} \\ \left.\frac{\partial L}{\partial \theta_{2}}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}^{0}} \\ \vdots\end{bmatrix}\)，\(\begin{bmatrix}\theta_{1}^{1} \\ \theta_{2}^{1} \\ \vdots \end{bmatrix}leftarrow\begin{bmatrix} \theta_{1}^{0} \\ \theta_{2}^{0} \\ \vdots \end{bmatrix}-\begin{bmatrix} \left.\eta \frac{\partial L}{\partial \theta_{1}}\right|_{\pmb{\theta}=\pmb{\theta}^{0}} \\ \left.\eta \frac{\partial L}{\partial \theta_{2}}\right|_{\pmb{\theta}=\pmb{\theta}^{0}} \\ \vdots \end{bmatrix}\)
  • 计算梯度\(\boldsymbol{g}=\nabla L(\pmb{\theta}^1)\)，\(\pmb{\theta}^2 \leftarrow \pmb{\theta}^1 - \eta \boldsymbol{g}\)
  • …

  在实际应用中，我们通常会把训练数据分成多个batch，1 epoch = 访问所有batch一次。1 epoch更新次数 = 样本数量 / batch size，batch size也是一个hyperparameter。

1.4 Improvement

1.4.1 Activation Function

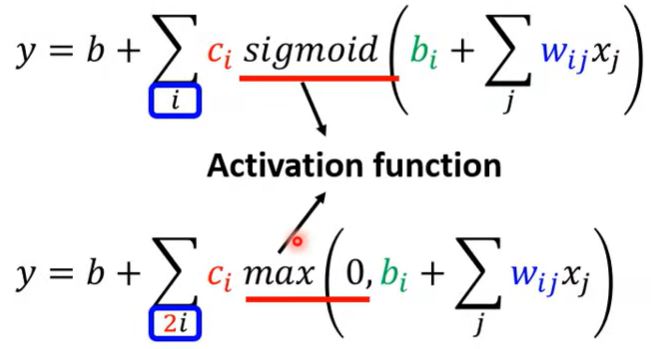
  前面我们用Sigmod函数来近似hard sigmod，其实还可以用Rectified Linear Unit (ReLU)来近似，即\(y = b + \sum_i c_i \operatorname{sigmoid}(b_i + \sum_j w_{ij} x_j) \rightarrow y = b + \sum_{2i} c_i \max(0, b_i + \sum_j w_{ij} x_j)\)。其中，Sigmod和ReLU都是激活函数。

1.4.2 Deep Learning

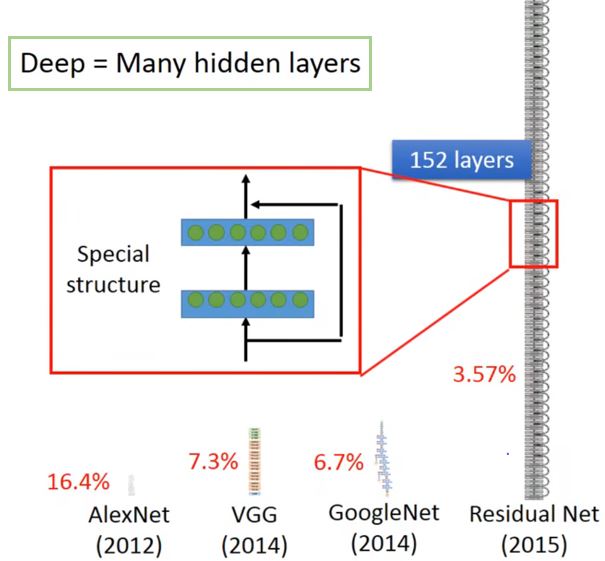
模型还可以如何改进呢？ — 增加层数

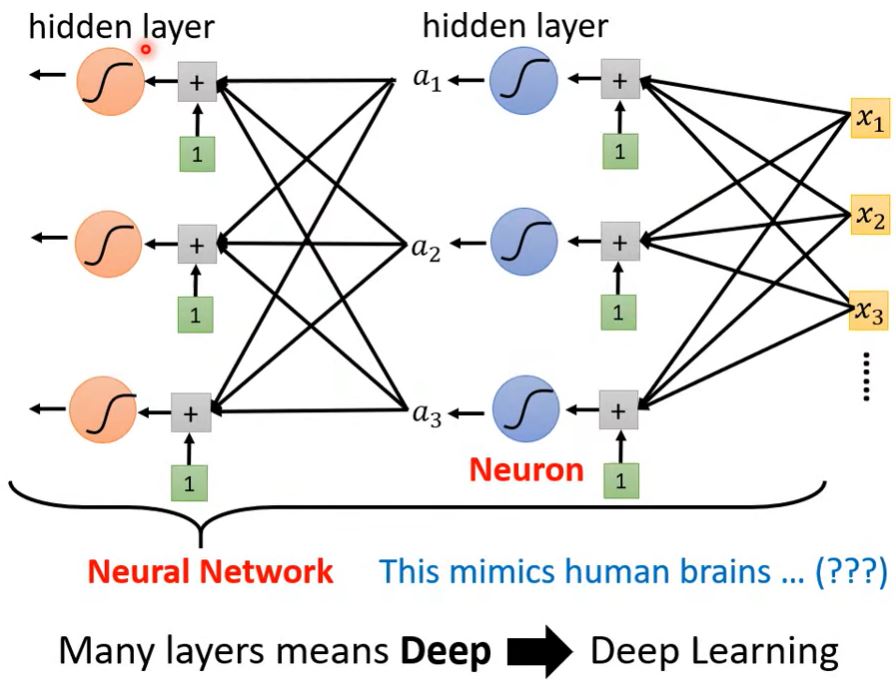
Deep = 很多隐藏层 为什么我们构建更深的网络，而不是增加输入的个数构建一个"fat"网络呢？

为什么不构建更深的网络呢？
— 更深的网络可能会在训练数据上取得更好的效果，但是在测试数据上反而表现更差，这种问题称为overfitting（过拟合）。

Introduction to DL *

Ups and downs of DL：

  • 1958：Perceptron (linear model)（感知机）
  • 1969：Perceptron有局限性
  • 1980s：Multi_layer perceptron
    • 与今天的DNN没有很大的区别
  • 1986：Backpropagation
    • 一般来说超过3层隐藏层没有什么更好的效果
  • 1989：1层隐藏层已经"足够好"，why deep?
  • 2006：RBM initialization（突破）
  • 2009：GPU
  • 2011：开始在语音识别领域流行起来
  • 2012：赢得了ILSVRC image competition

Three Steps for DL

Neural network

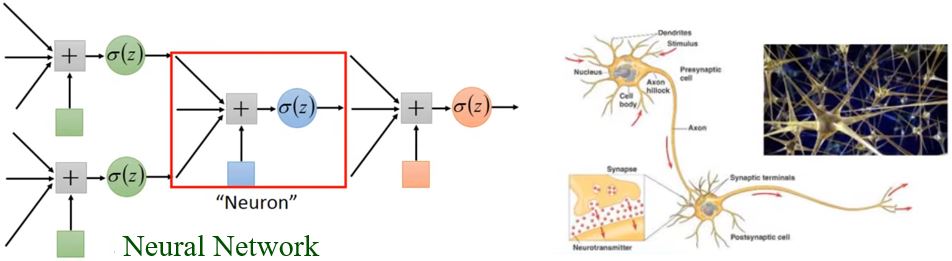
  不同的连接方式会导致不同的网络结构。
  网络参数\(\color{green}{\theta}\)：神经元中所有的weights和bias。

Fully connect feedforward network（全连接前馈网络）

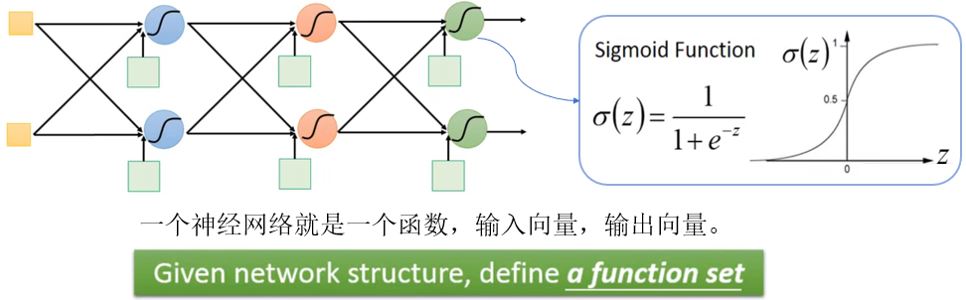
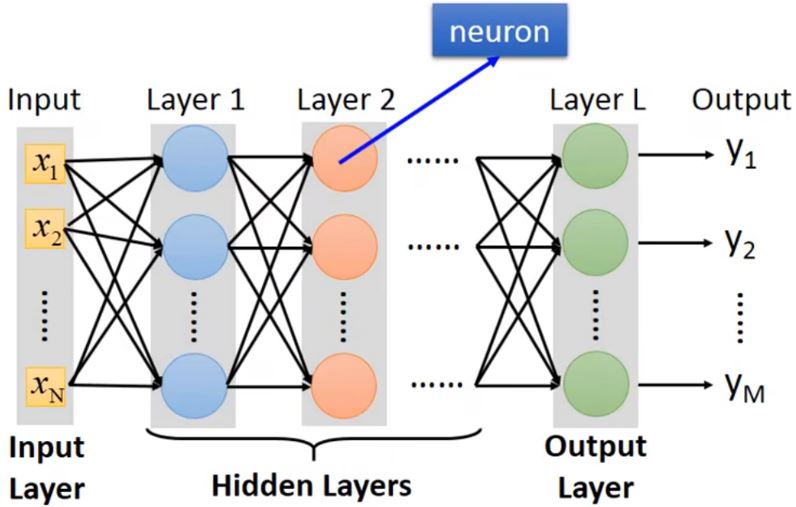
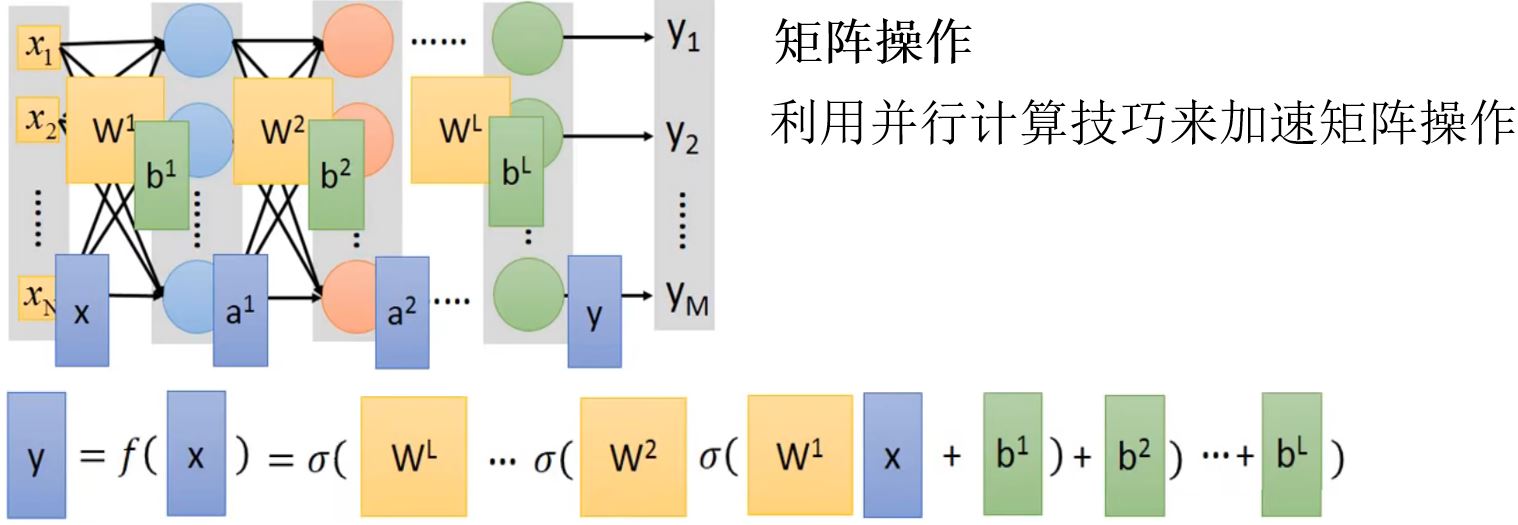
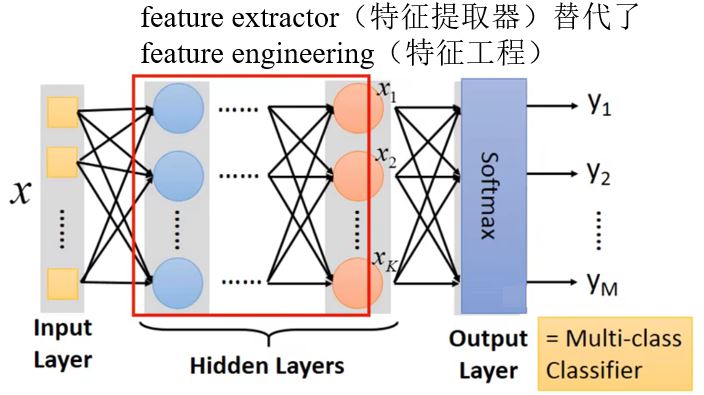
FAQ：
  多少层？每层多少个神经元？
  — trial and error + intuition
  结构可以自动决定吗？
  — e.g. Evolutionary Artificial Neural Networks.
  我们可以设计其它网络结构吗？
  — 可以，比如Convolutional Neural Network (CNN).

Goodness of fuction

  以把loss定义为交叉熵之和为例

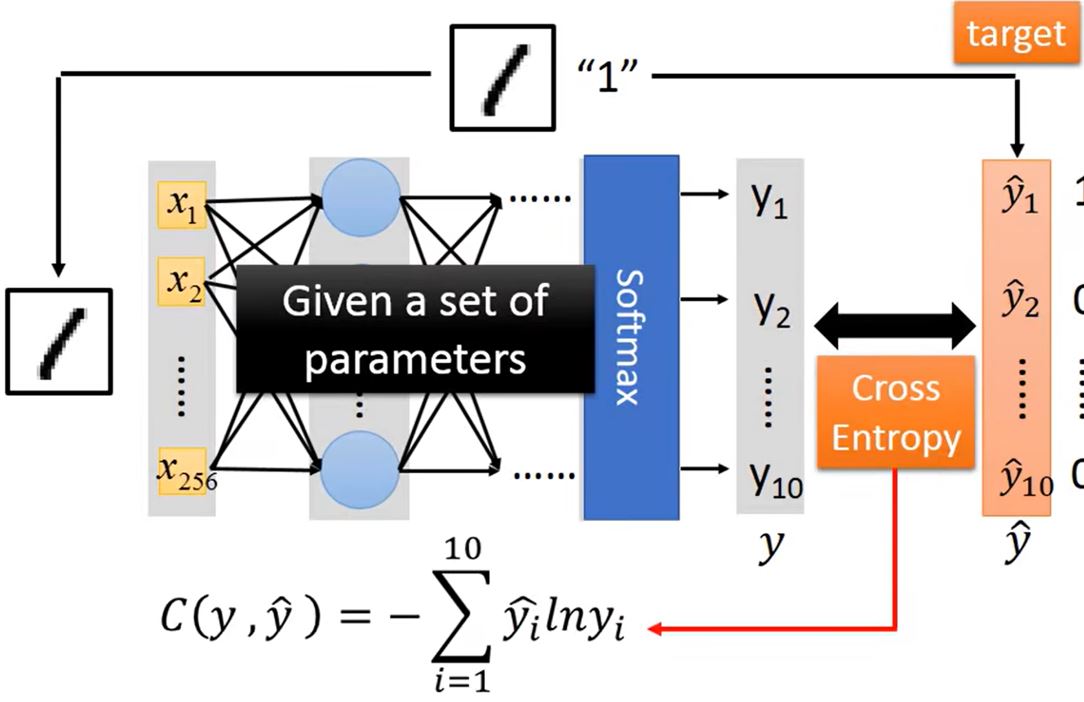
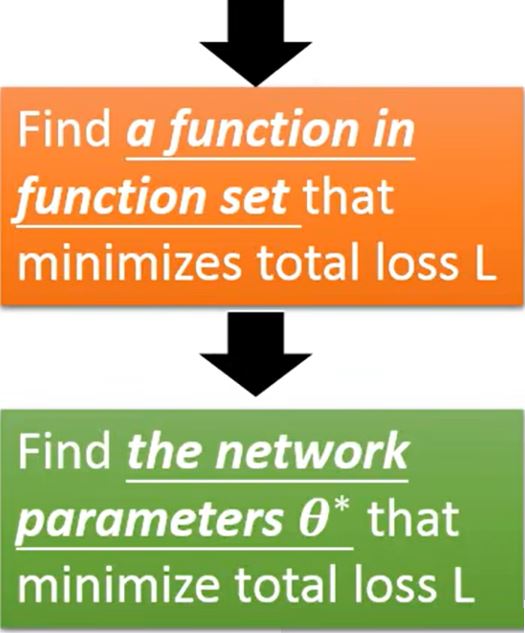
\[\color{green}{\text{Total loss} \quad \boxed{L = \sum_{n=1}^N C^n}}\]

Pick the best function

Gradient Descent

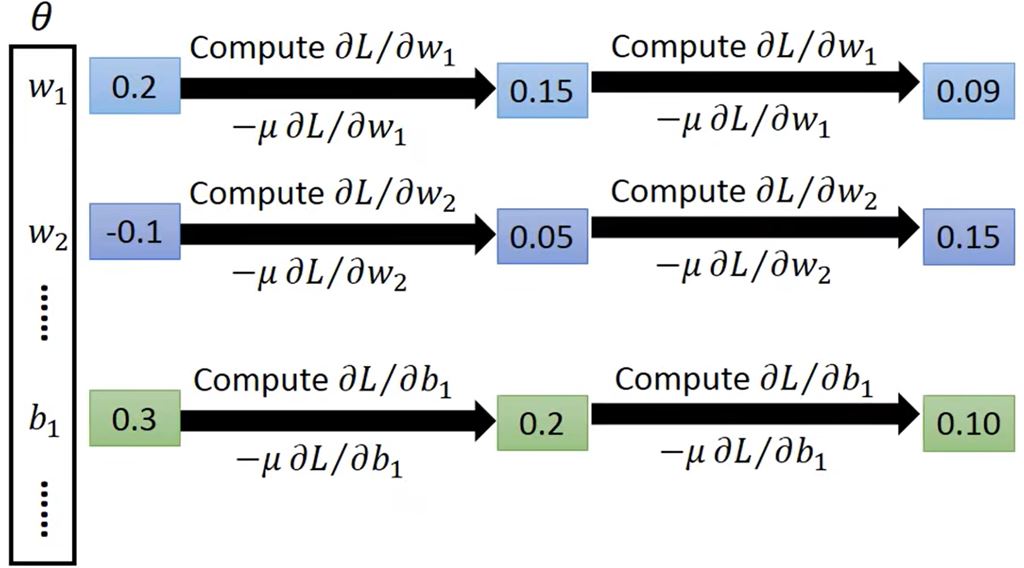
  这就是机器在深度学习中所做的"学习"，哪怕alphago也是这样学习的。

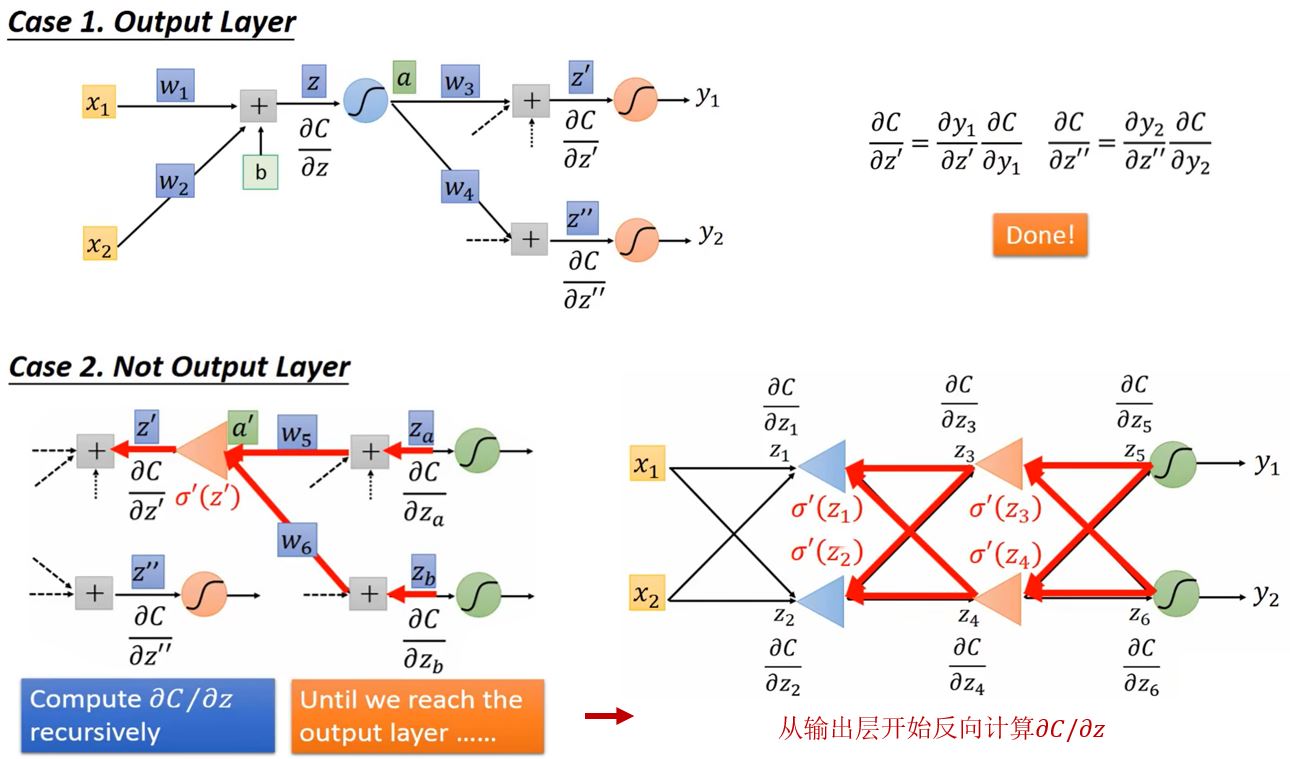
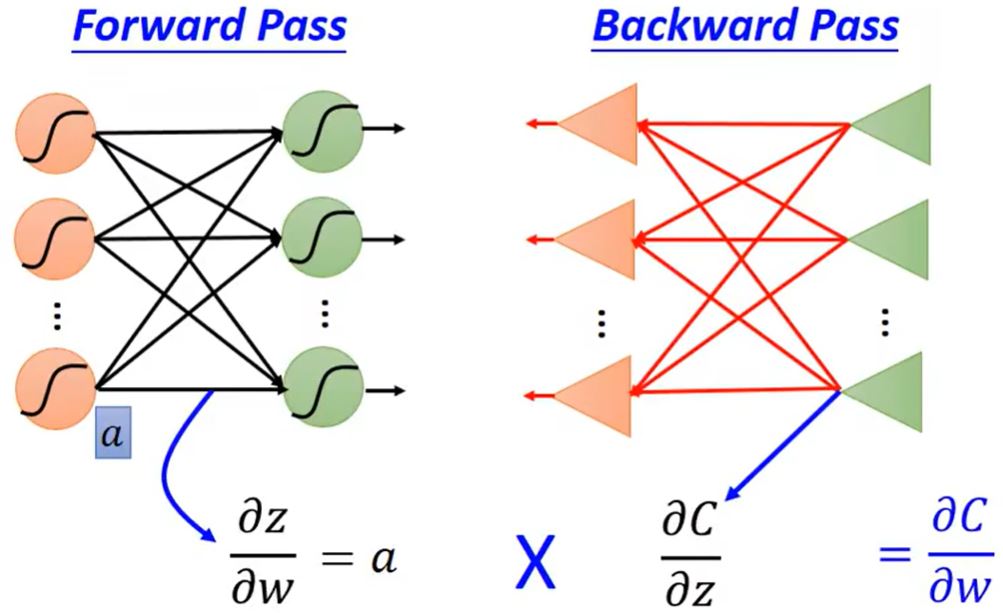
Backpropagation

  反向传播：在神经网络中计算梯度的高效方式。

Summary
计算梯度的toolkit
提示

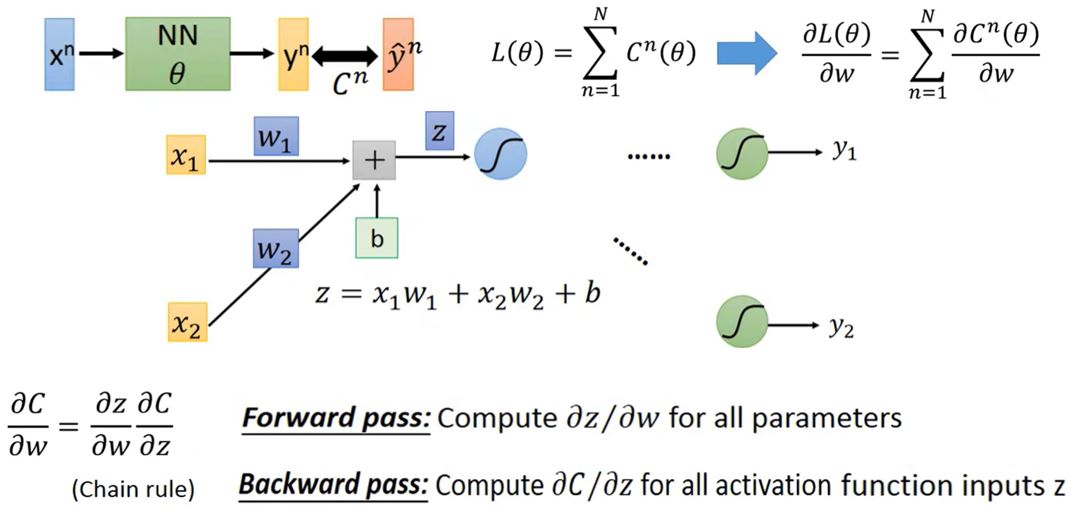
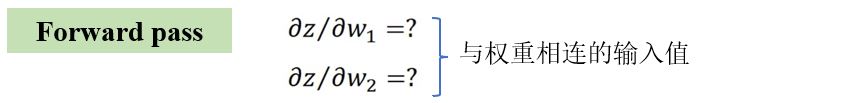
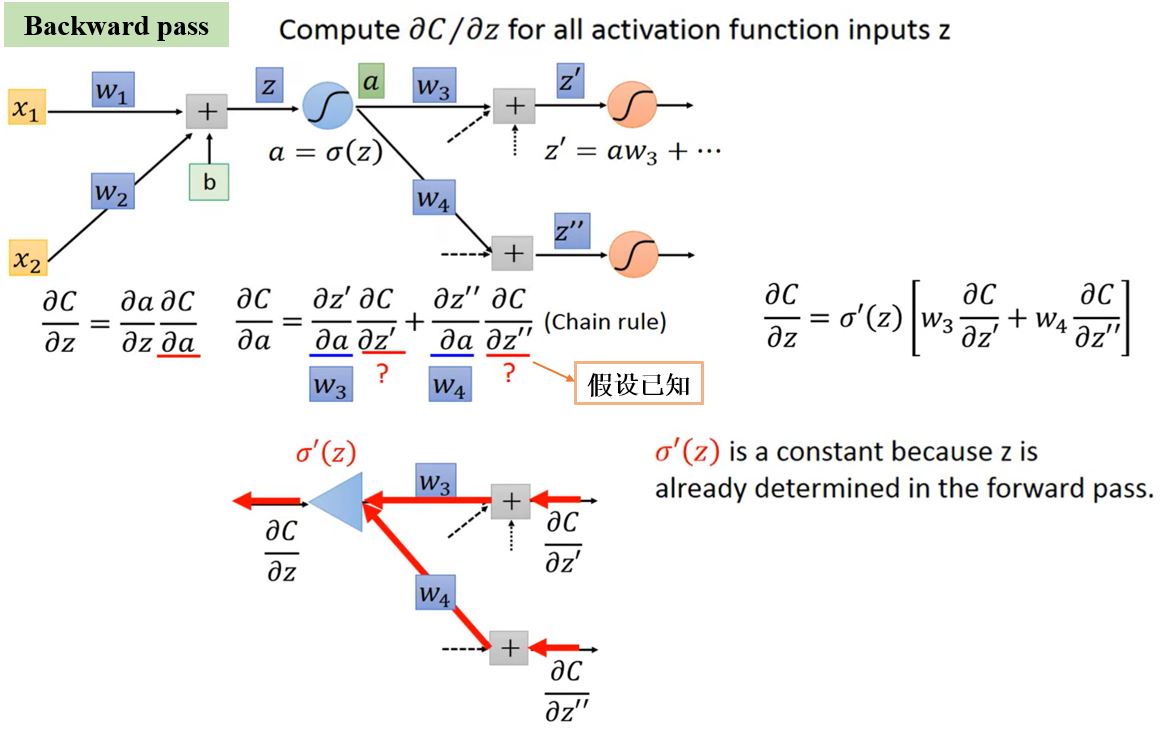
Deep is Better?

Univerality Theorom：任何连续函数\(f : \mathbb{R}^N \rightarrow \mathbb{R}^M\)可以由一个含有一层隐藏层的网络来实现（给定足够多神经元的情况下）。