What to Do If Training Fails

2.1 When Gradient is Small

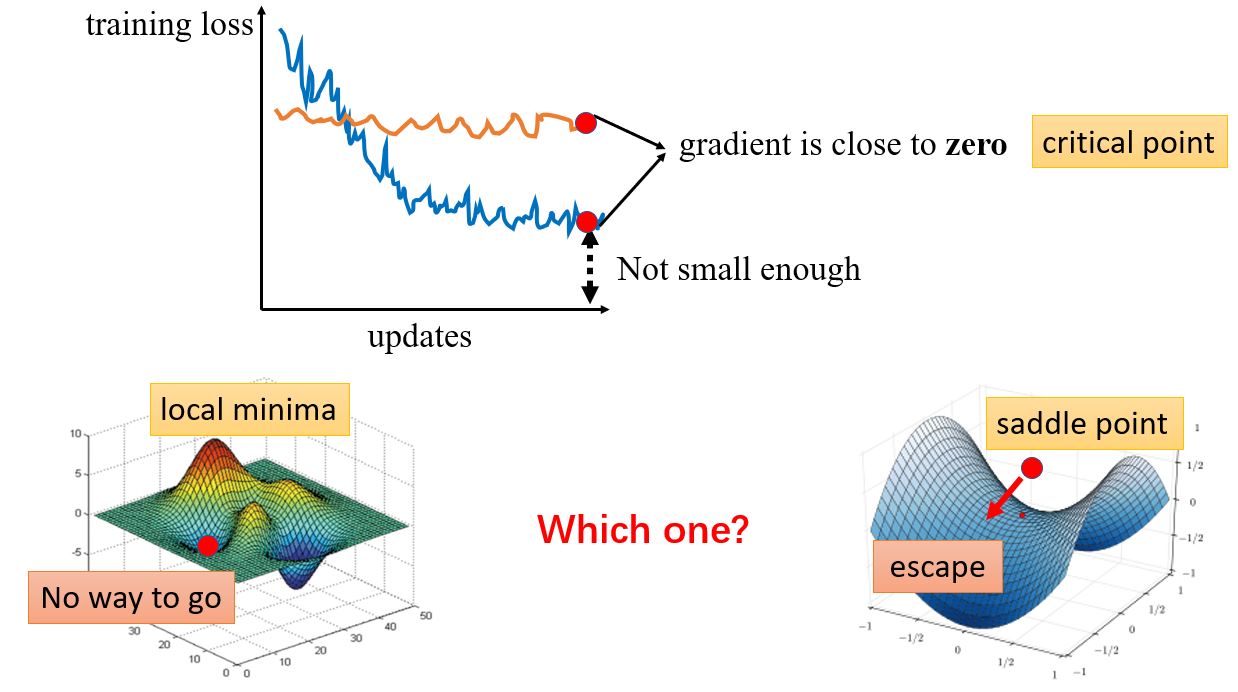
优化为什么会失败呢？
— 梯度为零，有两种情况：局部极小值和鞍点，这两种点统称为critical point（驻点）。在局部极小值点无路可走，而鞍点只要能够逃离的话还是可以继续下降的。

  如何判断是局部极小还是鞍点呢？

2.1.0 Local minima & Saddle point

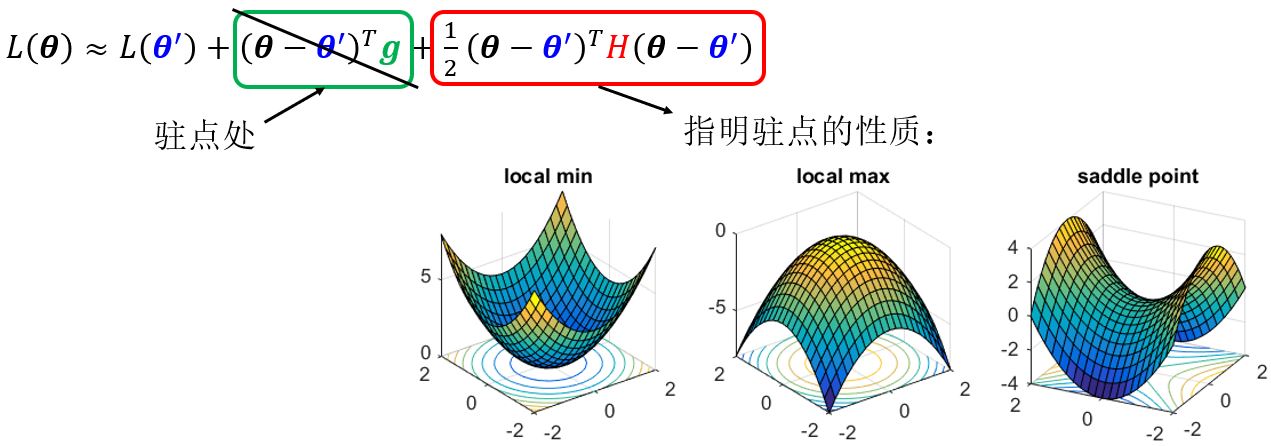
Taylor series approximation

Hessian

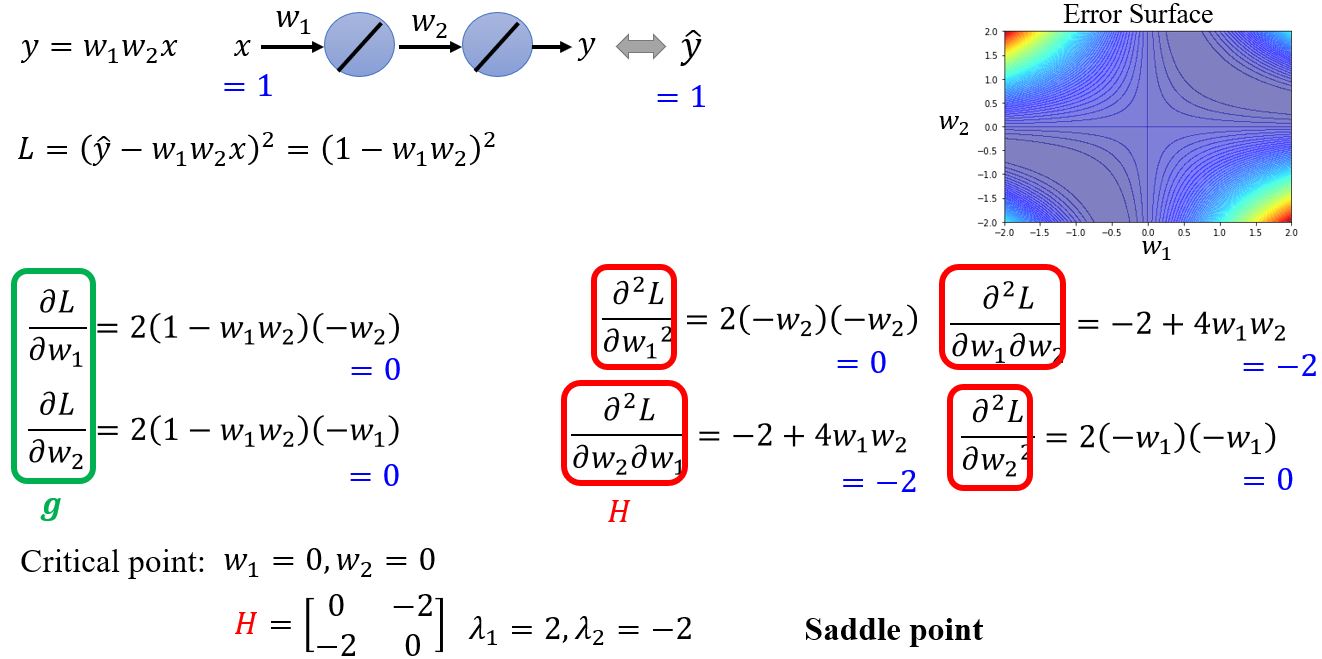
例：

Don't afraid of saddle point?

  \(H\)或许可以告诉我们参数更新的方向！

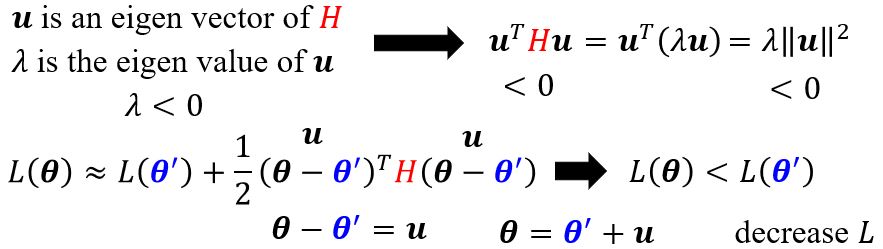
例：

2.1.1 Saddle point v.s. Local minima

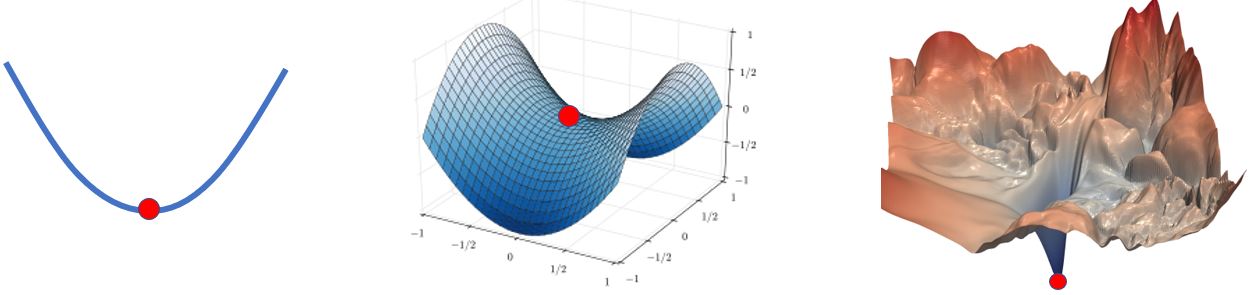
  低维空间里的局部极小值点可能只是高维空间中的一个鞍点，那么当你有很多参数的时候，会不会局部极小值点就很少见了呢？

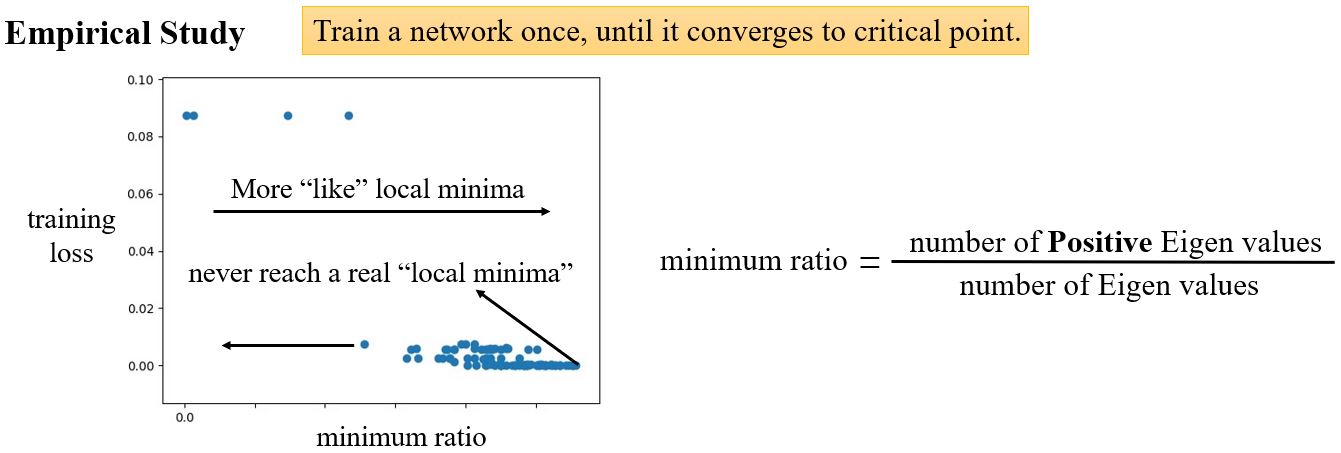
2.1.2 Small gradient

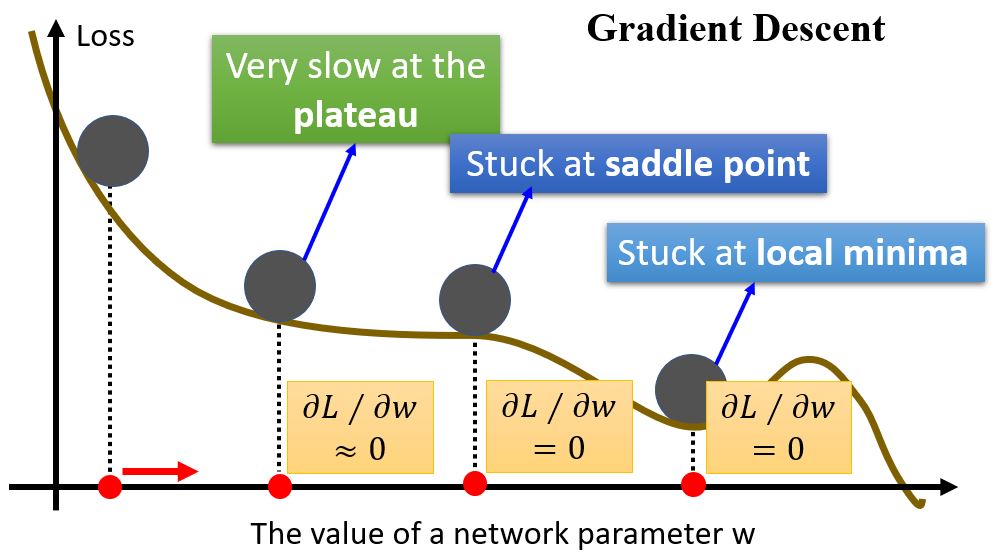
2.2 Tips: Batch & Momentum

2.2.1 Batch

Review: Optimization with batch

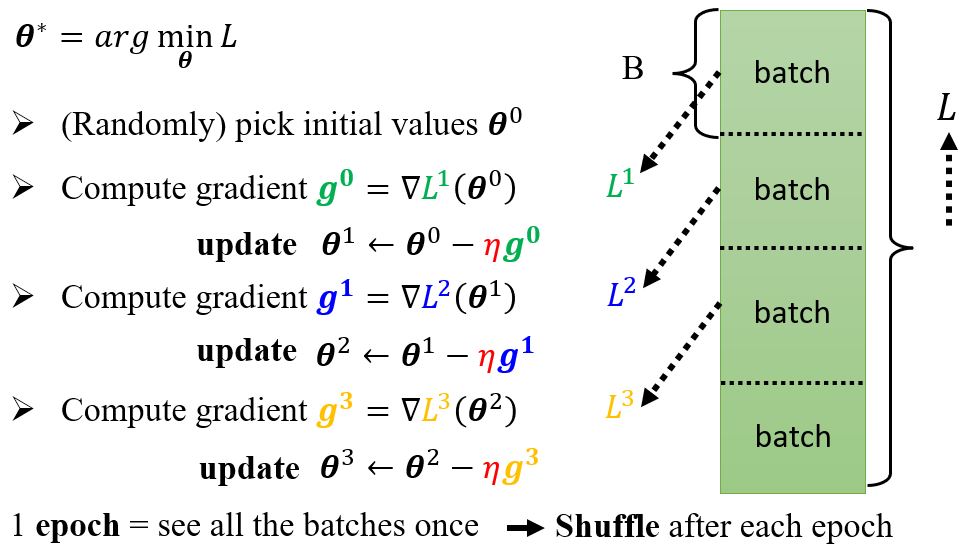
Small batch v.s. Large batch

  考虑有20个样本的情况（\(N=20\)）：

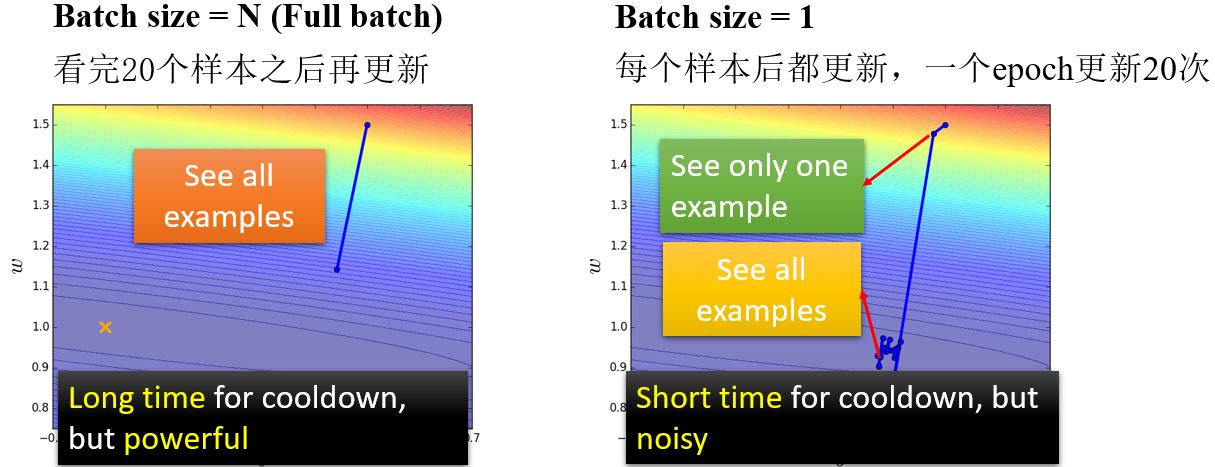
左边的方法更新的一步更稳定，但是看起来花的时间长。但是实际上，考虑到并行运算，大的batch size在计算梯度的时候并不需要更长的时间。

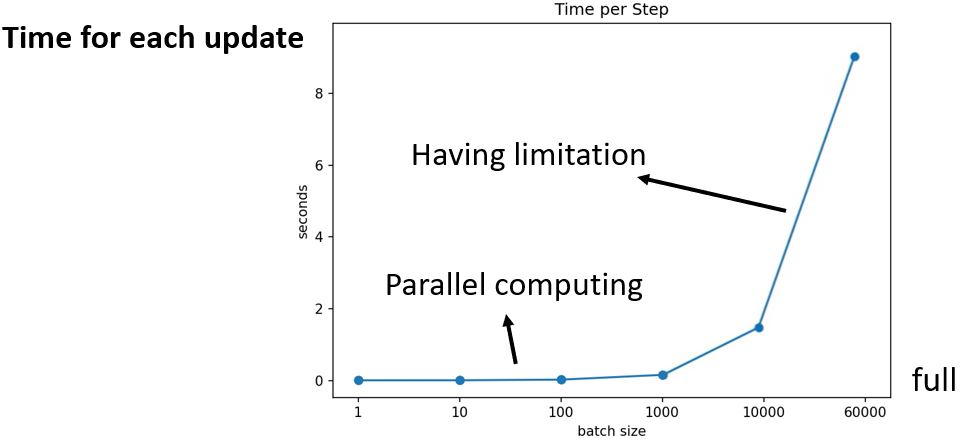
用Tesla V100 GPU在MNIST数据集上每次更新的时间随batch size变化的情况

  并且，较小的batch一次epoch所需的时间反而更长（花更多的时间来把所有的数据看一遍）。

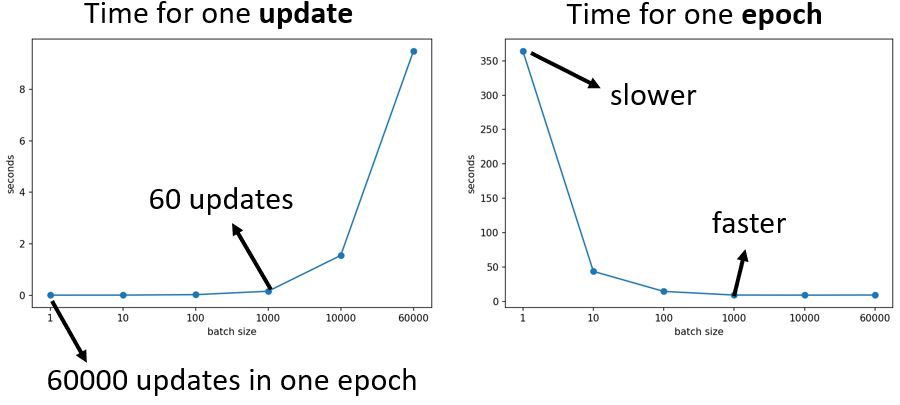
  那么大的batch就一定好吗？

不同训练集上准确率随batch size变化的情况

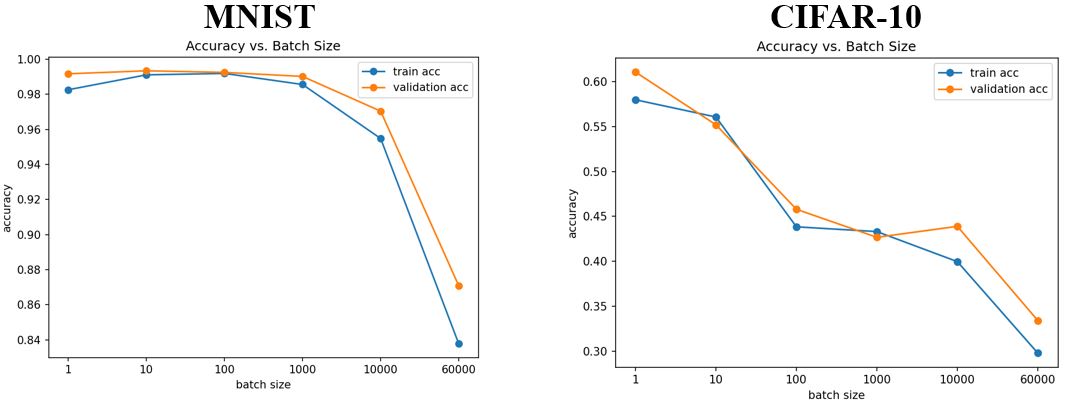
从上图可以看出，小的batch size的表现更好。那么大的batch size有什么问题呢？ — Optimization Fails（因为用的都是一样的模型，所以不是因为model bias）

  • 小的batch size性能更好
  • "noisy"的更新有利于训练

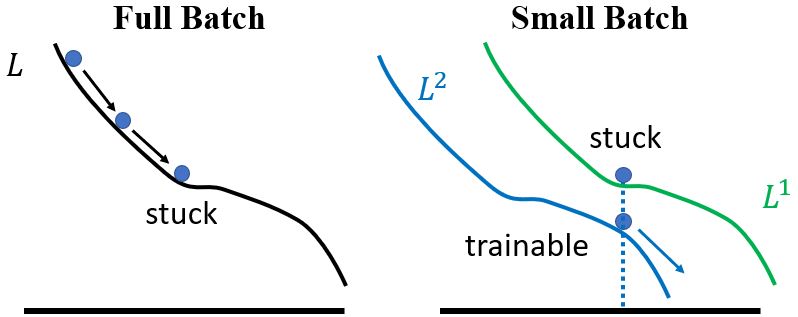
此外，small batch在测试数据上表现也更好。

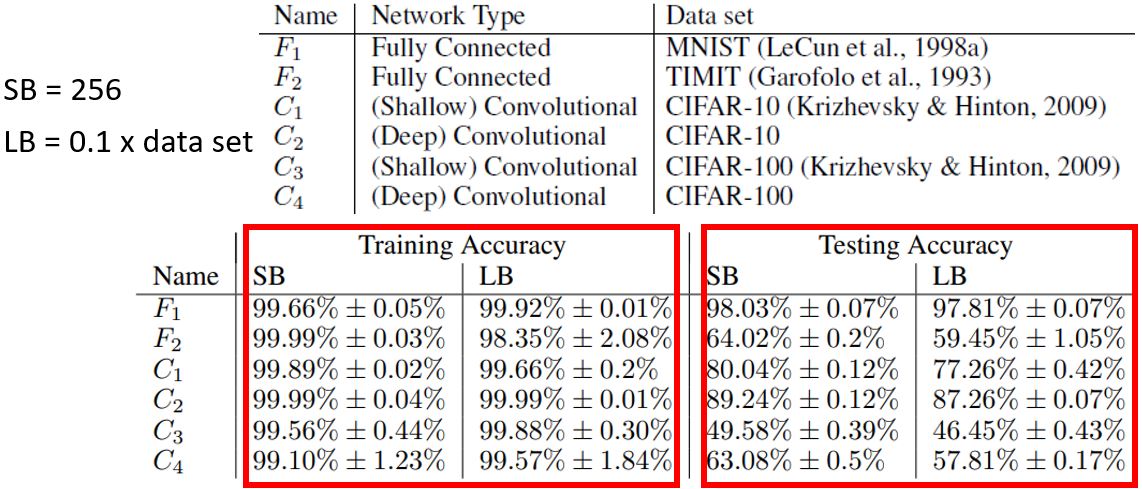
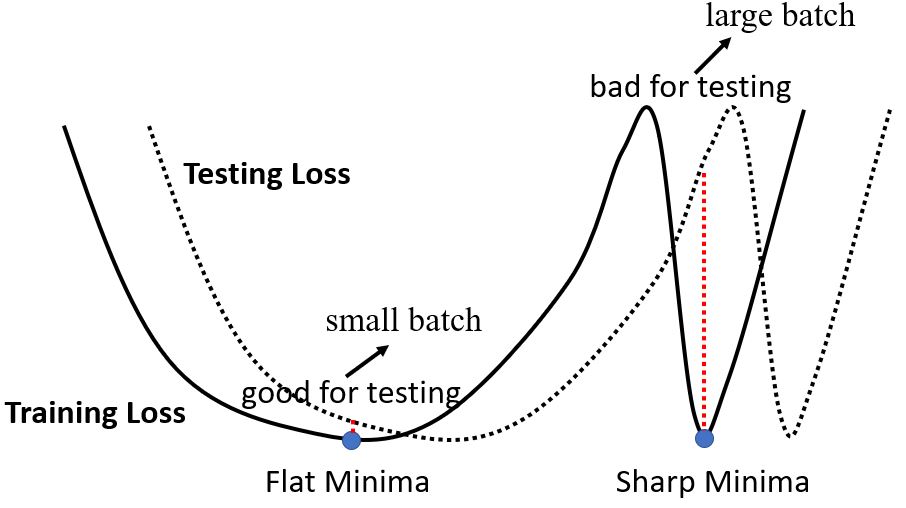
On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima中的结果

  Small Batch v.s. Large Batch，两者各有优缺点，所以batch size是一个需要我们决定的hyperparameter。

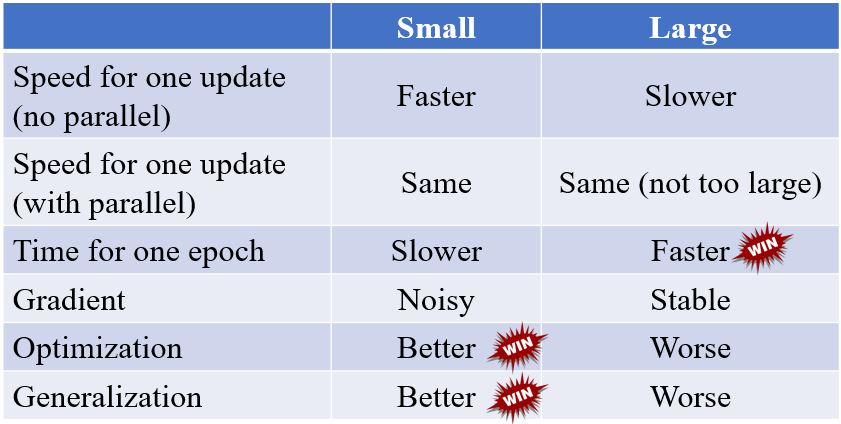
两者兼得？
  Large Batch Optimization for Deep Learning: Training BERT in 76 minutes
  Extremely Large Minibatch SGD: Training ResNet-50 on ImageNet in 15 Minutes
  Stochastic Weight Averaging in Parallel: Large-Batch Training That Generalizes Well
  Large Batch Training of Convolutional Networks
  Accurate, large minibatch sgd: Training imagenet in 1 hour

2.2.2 Momentum

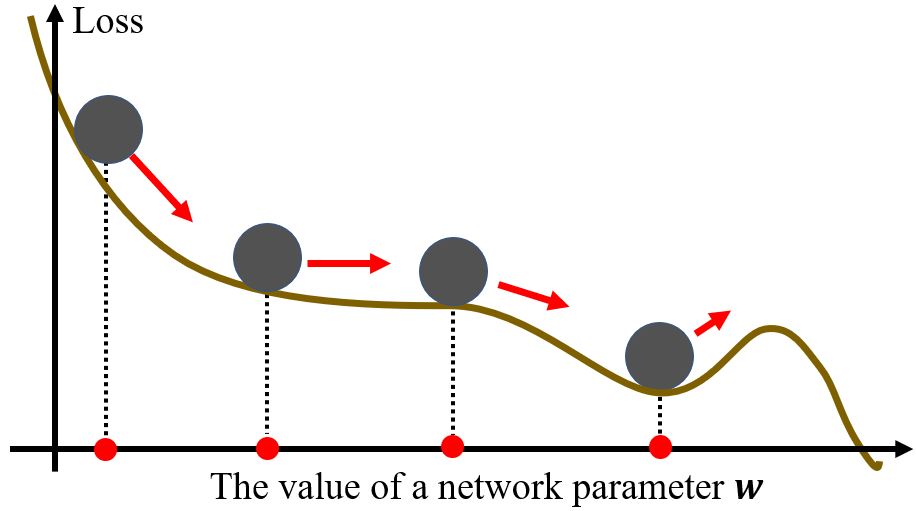
  考虑物理世界，error surface就是斜坡，而参数是一个球，球从斜坡上滚下来，由于惯性的存在，它不一定会被鞍点或局部极小点卡住。

(Vanilla) Gradient descent

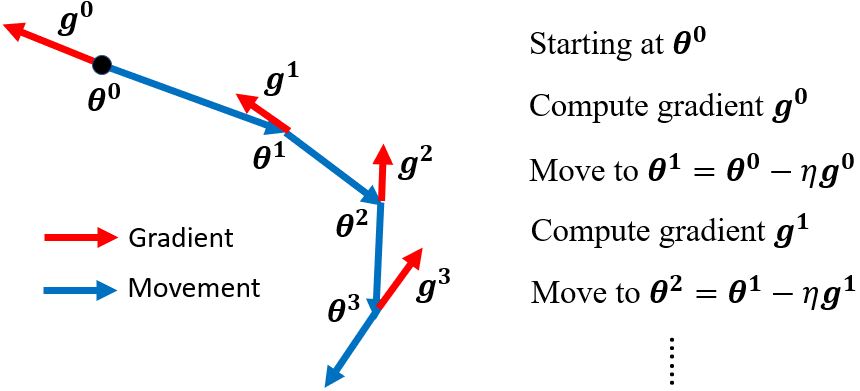
  一般的梯度下降：计算初始点处的梯度，然后往梯度的反方向更新一次参数，得到一组新的参数，然后计算梯度并往梯度的反方向更新一次参数……不断重复这个过程。

Gradient descent + Momentum

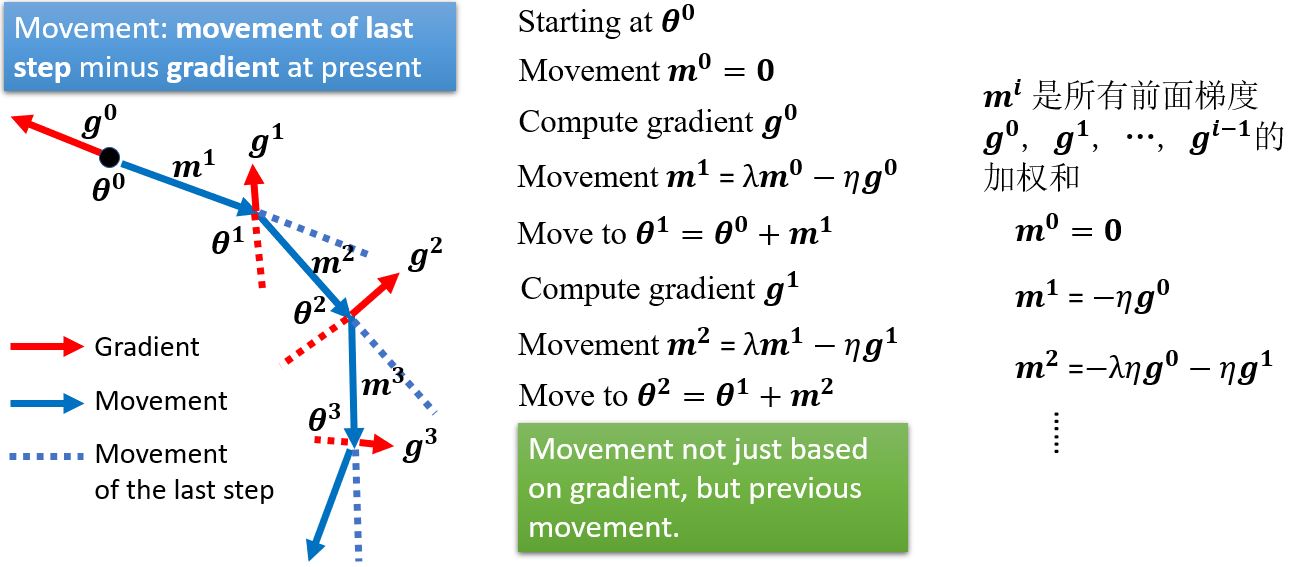
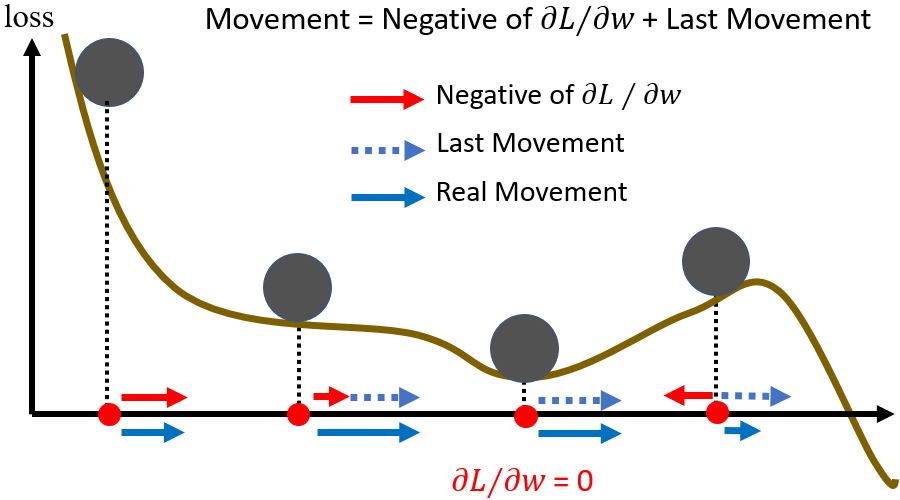
2.2.3 Concluding remarks

  • 驻点处梯度为零
  • 驻点可能是鞍点或局部极小值点
    • 可以利用Hessian矩阵来区别
    • 沿着Hessian矩阵的特征向量可以逃离鞍点
    • 局部极小点可能是很少见的
  • 更小的batch size和momentum可以帮助逃离驻点

2.3 Tip: Adaptive Learning Rate

2.3.1 Training stuck ≠ Small gradient

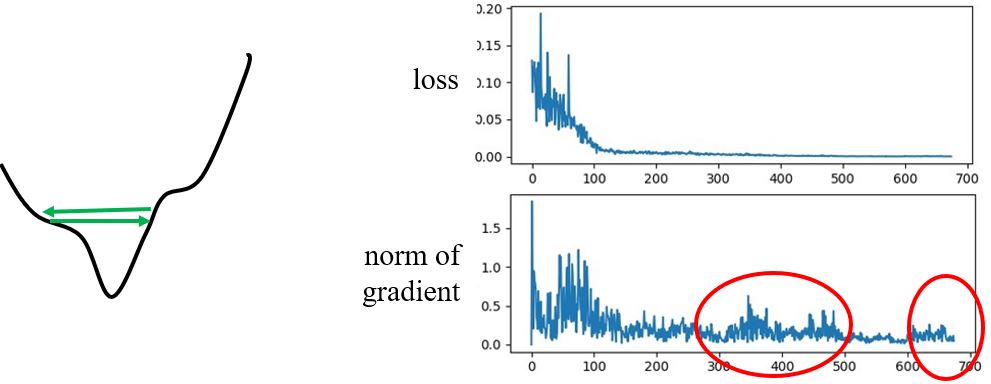
  人们总是以为训练卡住是因为参数到了驻点附近，但是实际计算一下梯度大小的变化，可以发现其实梯度并没有真的变得很小。

  如果说训练停住往往不是因为驻点，那是因为什么呢？以一个凸的error surface为例，从头到尾采用同一个学习率是得不到好的结果的。

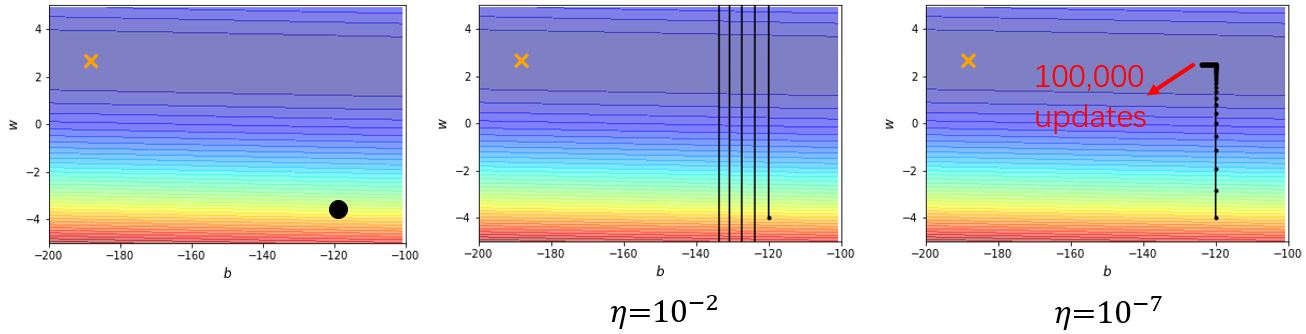
2.3.2 Adaptive learning rate

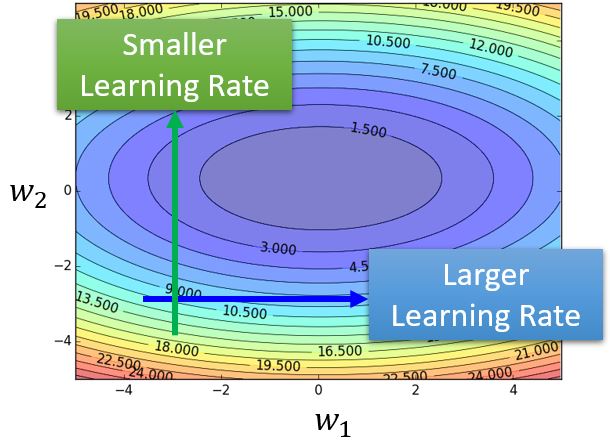
  不同的参数需要不同的学习率。如果在某个方向上梯度的值很小，梯度非常平坦，那么我们会希望学习率大一点；反之，如果在某个方向上非常陡峭，那么会希望学习率小一点。那么如何来自适应地调整学习率呢？

  以某一个参数\(\pmb{\theta}\)更新的过程为例。原来\(\pmb{\theta}\)的更新为 \(\pmb{\theta}_i^{t+1} \leftarrow \pmb{\theta}_i^t - \eta g_i^t\)，\(\boldsymbol{g}_i^t = \left. \frac{\partial L}{\partial \pmb{\theta}_i} \right\vert_{\pmb{\theta} = \pmb{\theta}^{t}}\)。现在，将\(\eta\)这项改为\(\frac{\eta}{\sigma_i^t}\)，这是一个与参数相关的学习率。

Root mean square

AdaGrad中采用的方法

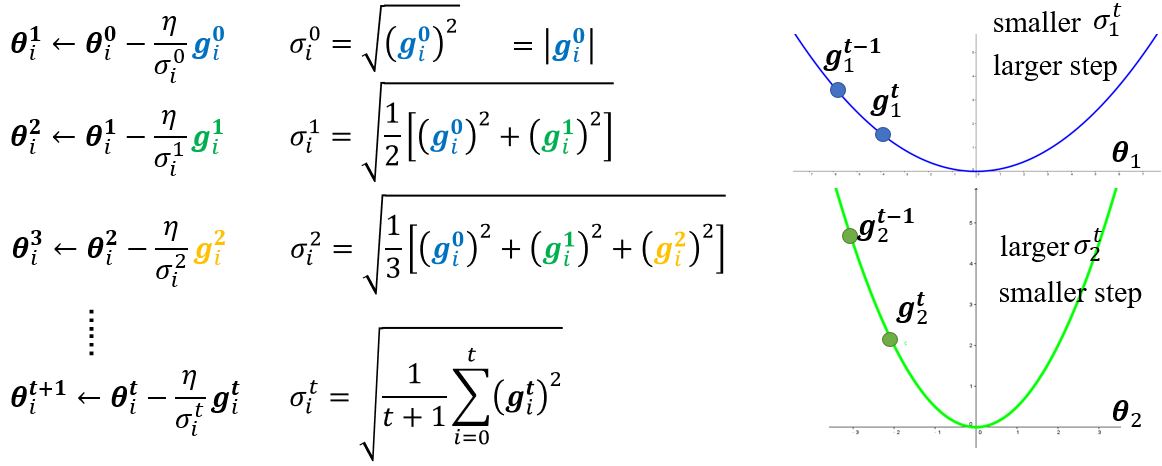
  在AdaGrade中，即使是同样的参数，所需的学习率也会随着时间的改变而变化。

Learning rate adapts dynamically

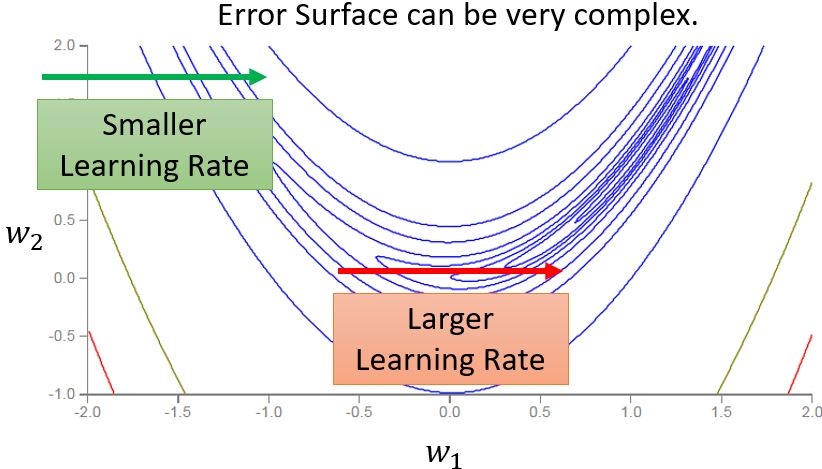
  之前，我们似乎假设同一个参数对应的梯度都是差不多的值。实际上，以上图为例，同一个参数我们也期望有不同的学习率，那就需要学习率能够动态地适应调整。

RMSProp

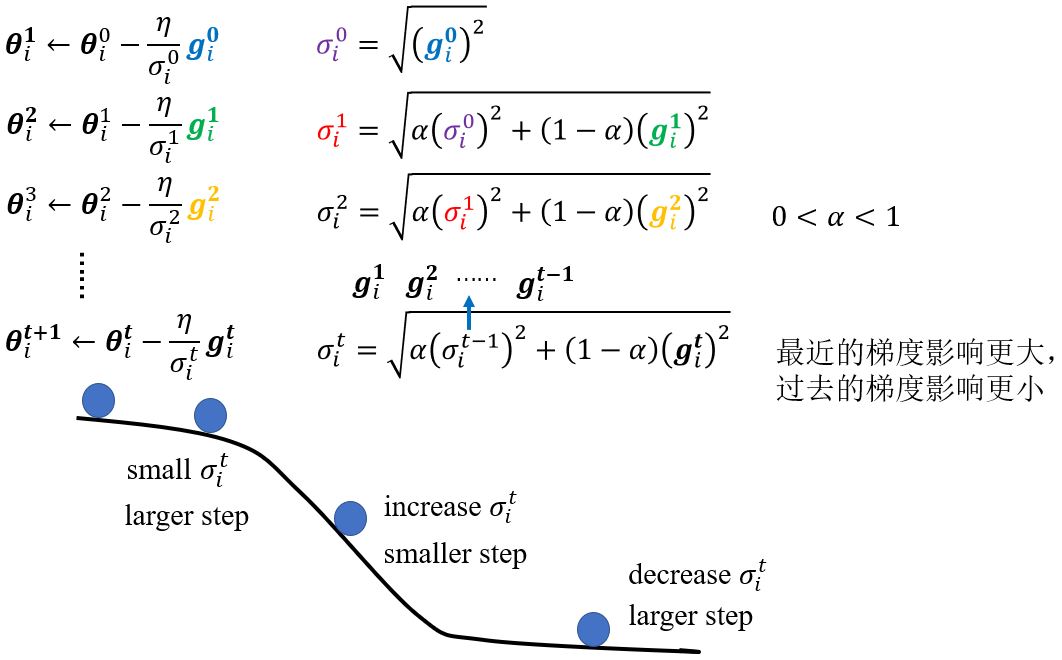
Adam: RMSProp + Momentum

原文：ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION

2.3.3 Learning rate scheduling

用AdaGrad的方法来调整学习率的结果

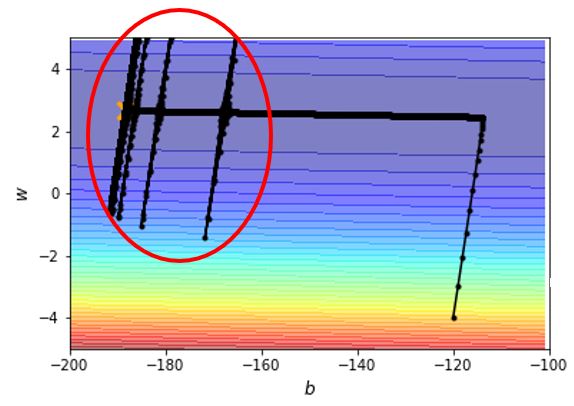
  如何解决这种震荡问题呢？

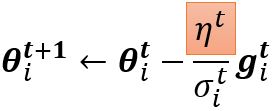
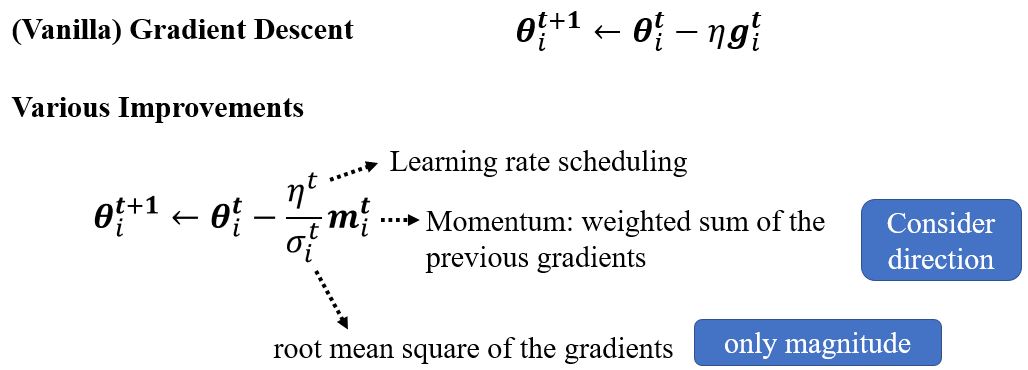
2.3.4 Summary of optimization

2.4 Loss Function: Classification