Potential Functions

本章介绍了适用于更一般的构型空间的导航规划器，包括适用于多维空间和非欧几里得空间的。

势函数（potential function）\(U:\mathbb{R}^m \rightarrow \mathbb{R}\)是可微的实值函数。势函数的值可以看作能量，势的梯度相应地可以看作力。梯度（gradient）\(\Delta U(q) = DU(q)^T = \left[ \frac{\partial U}{\partial q_1}(q), \ldots, \frac{\partial U}{\partial q_m}(q) \right]^T\)是指向\(U\)增长的局部最快方向的向量(更严密的定义见附录C.5)。利用梯度，可以定义向量场（vector filed），为流形上的每个点分配一个向量。当\(U\)是能量的时候，梯度向量场有如下性质：闭合回路的功为零。

势函数法指引机器人的方式如图4.1所示。

注意

本章主要讨论一阶系统（i.e. 忽略动力学），所以把梯度看成速度向量而非力向量。

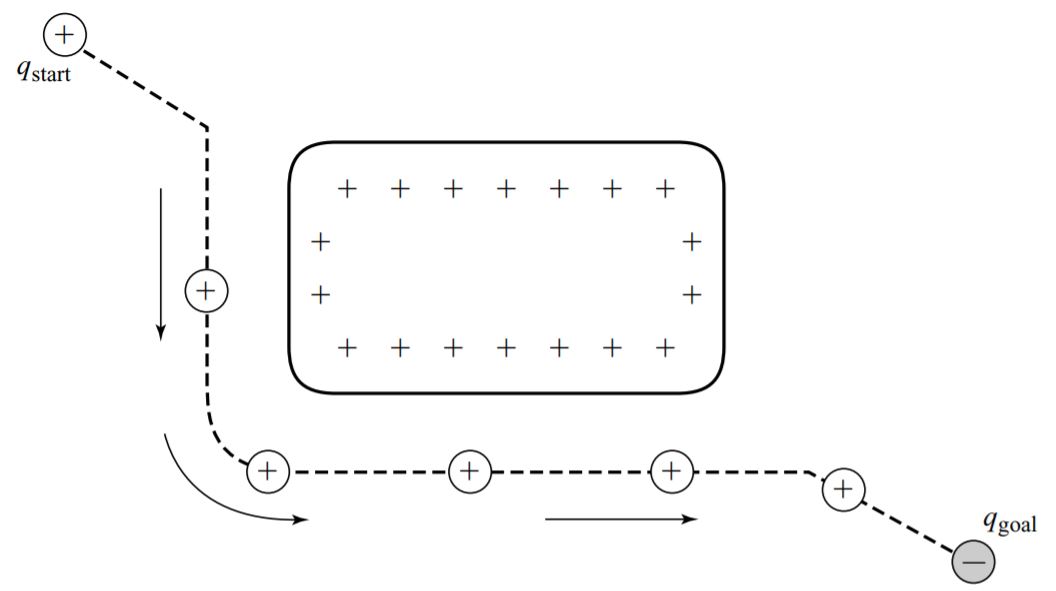
Fig 4.1 负电荷吸引，正电荷排斥，生成了一条绕开障碍物到达目标点的路径，由虚线表示

势函数可以看作地形，机器人在上面从高值态运动到低值态。机器人沿着势函数的负梯度下降，沿着这种路径的方法被称为梯度下降（gradient descent），i.e. \(\dot{c}(t) = - \nabla U(c(t))\)。

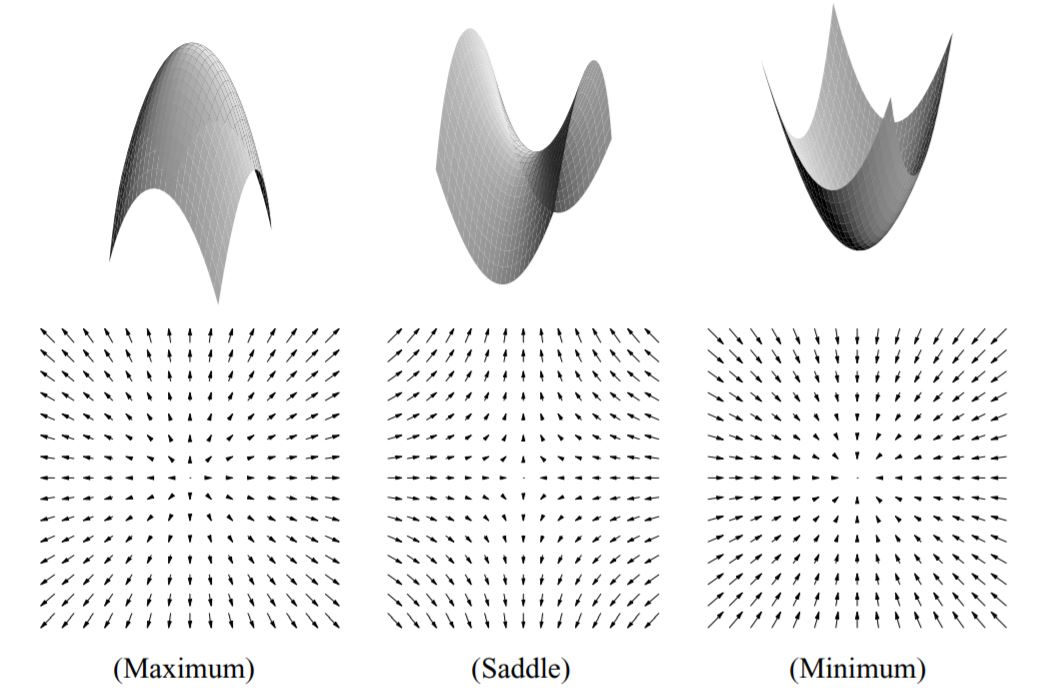
机器人会停在梯度为零的点\(q^*\)（\(\nabla U(q^*) = 0\)），这种点称为临界点。该点的类型（最大值、最小值或鞍点，如图4.2所示）由二阶微分决定。对于实值函数，二阶微分为Hessian矩阵。若Hessien在\(q^*\)处非奇异，则\(q^*\)处的临界点是非退化的，表明该点是孤立的。Hessian正定对应局部极小值；负定对应局部极大值。一般来说，只考虑Hessian非奇异的势函数，i.e. 只含孤立临界点的势函数，这样的势函数没有平坦的部分。

补充

对于梯度下降法，无需计算Hessian，因为机器人一般只能在局部极小值点终止运动，而非局部极大值点或鞍点。只有局部极小值点才是稳定的，因为机器人在该点受到扰动后还是会回到这个极小值点。目标点应该落在局部极小值点。

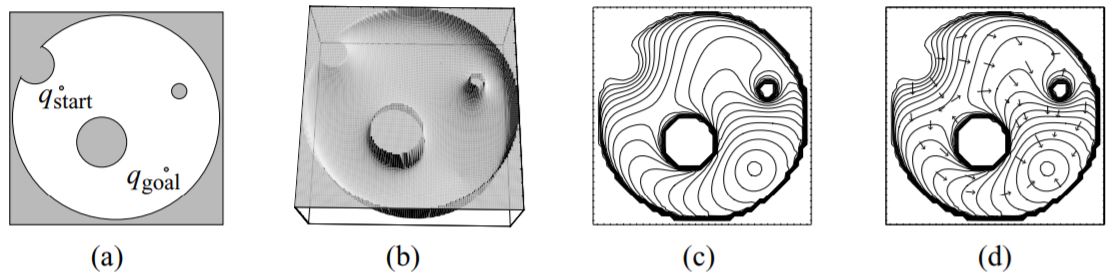
Fig 4.3 (a)含有三个障碍物的圆形边界的构型空间；(b)能量面的势函数； (c)能量面等值线图；(d)势函数的梯度向量

有许多有效且可以在线计算的势函数，但是它们有一个共通的问题：局部极小值的位置和目标不匹配。也就是说，很多势函数无法得出完备的路径规划器。解决这个问题有两种思路：1.利用基于采样的规划器对势场进行增广；2.定义只有一个局部极小值点的势函数，被称为navigation function。尽管完备（或解析完备），这些方法都需要在规划前对构型空间有充分的了解。

本章讨论的算法都是可以用于任意维空间的，除非特殊说明。本章还对如何实现在平面上操作的移动底盘（i.e. 二维欧式构型空间内的一个点）。

4.1 Additive Attractive/Repulsive Potential

\(\mathcal{Q_{free}}\)中最简单的势函数就是attractive/repulsive potential。目标会吸引机器人，而障碍物会排斥它，它们共同作用引导机器人远离障碍到达目标点。势函数可以构造成二者之和\(U(q) = U_{att}(q) + U_{rep}(q)\)。

The Attractive Potential

势场\(U_{att}\)需要满足以下标准：1.\(U_{att}\)应关于与\(q_{goal}\)的距离单调增加。最简单的一种就是conic(圆锥曲线) potential，计算到目标的比例距离，i.e. \(U(q) = \xi d(q,q_{goal})\)。其中，\(\xi\)是用来缩放吸引势的作用的参数。吸引梯度为\(\nabla U(q) \frac{\xi}{d(q,q_{goal})} (q-q_{goal})\)。梯度向量按大小\(\xi\)指向远离目标的方向，在构型空间内除了目标点外所有点，目标点处没有定义。从非目标点处开始，沿着负梯度，有一条指向目标的路径。

选上面这种势函数在进行数值实现时，梯度下降会有很多问题，因为吸引势在原点是不连续的。因此，我们倾向于选择连续可微的势函数，这样吸引势的大小随着机器人接近\(q_{goal}\)变小。这种势函数最简单的就是随与目标的距离二次增长的，e.g. \(U_{att}(q) = \frac{1}{2} \xi d^2 (q,q_{goal})\)，其梯度为\(\nabla U_{att}(q) = \frac{1}{2} \xi \nabla d^2 (q,q_{goal}) = \xi (q,q_{goal})\) ，是从\(q\)开始指向远离\(q_{goal}\)方向的向量，大小与二者之间的距离成正比。也就是说，当机器人离目标较远时，速度较快，距离变进时，速度会变慢。

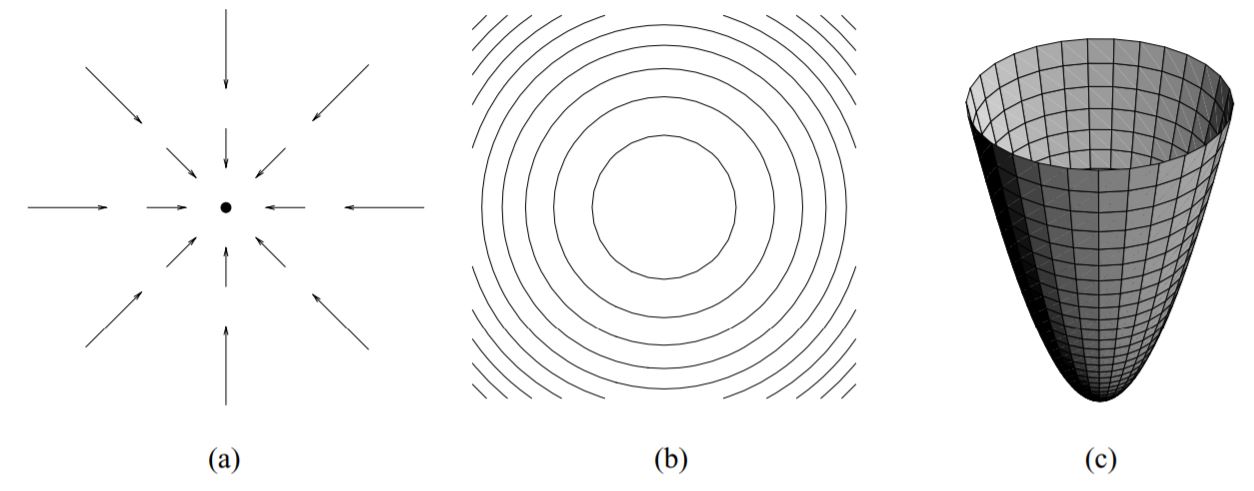
这种势函数当机器人离目标很远的时候会生成过大的速度，所以我们可以把这两种函数结合起来。

\[U_{att}(q) = \begin{cases} \frac{1}{2} \xi d^2 (q,q_{goal}) & , \quad d(q,q_{goal}) \le d_{goal}^* \\ d_{goal}^* \xi d(q,q_{goal}) - \frac{1}{2} \xi (d_{goal}^*)^2 & , \quad d(q,q_{goal}) \gt d_{goal}^* \end{cases} \tag{4.2}\] \[\nabla U_{att}(q) = \begin{cases} \xi (q-q_{goal}) & ,\quad d(q,q_{goal}) \le d_{goal}^* \\ \frac{d_{goal}^* \xi (q-q_{goal})}{d(q,q_{goal})} & , \quad d(q,q_{goal}) \gt d_{goal}^* \end{cases} \tag{4.3}\]

其中，\(d_{goal}^*\)是规划器在圆锥曲线和二次曲线之间切换时对应的与目标点的距离。

The Repulsive Potential

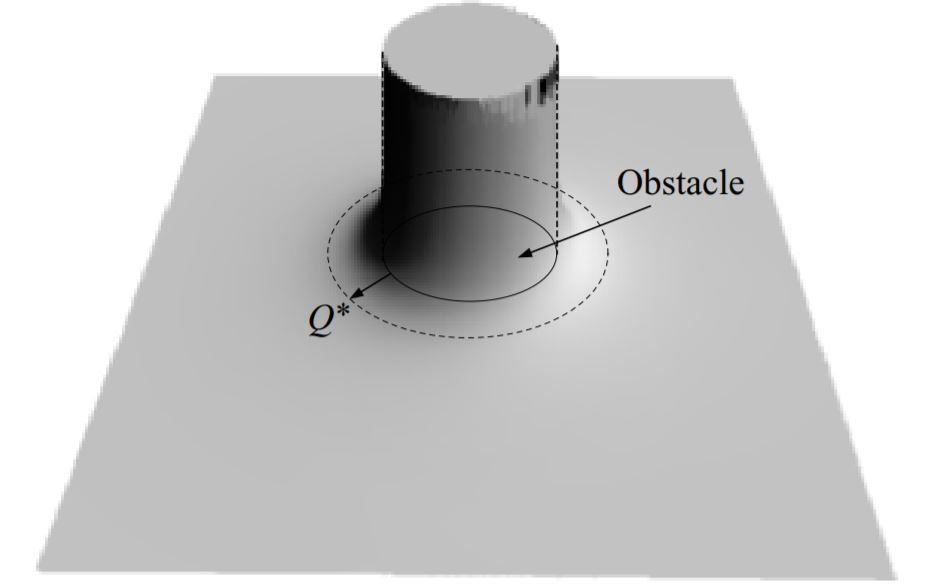
排斥势会使机器人远离障碍物，排斥力的大小与机器人离障碍物的距离有关。因此，排斥势往往用与最近的障碍物的距离\(D(q)\)来定义

\[U_{rep}(q) = \begin{cases} \frac{1}{2} \eta \left( \frac{1}{D(q)} - \frac{1}{\mathcal{Q}^*} \right)^2 \quad , & D(q) \le \mathcal{Q}^* \\ 0 \quad , & D(q) \gt \mathcal{Q}^* \end{cases} \tag{4.4}\]

其梯度为

\[\nabla U_{rep}(q) = \begin{cases} \eta \left( \frac{1}{\mathcal{Q}^*} - \frac{1}{D(q)} \right) \frac{1}{D^2(q)} \nabla D(q) \quad , & D(q) \le Q^* \\ 0 \quad , & D(q) \gt Q^* \end{cases} \tag{4.5}\]

其中，\(\mathcal{Q} \in \mathbb{R}\)使得机器人可以忽略距离足够远的障碍，\(\eta\)可以看作是排斥梯度的增益。这些标量通常通过试错和误差来决定。（如图4.5所示。）

Fig 4.6 距离为到障碍物上最近的点的距离。梯度是指向背离最近点方向的单位向量。

在对这个方法进行数值实现的时候，路径可能会在某个点周围振荡，因为它们与障碍的距离相等，i.e. 不平滑的\(D\)上的点。为了避免这种振荡，用单个障碍物的距离来重新定义排斥势函数，其中\(d_i(q)\)是与障碍\(\mathcal{QO_i}\)的距离，如

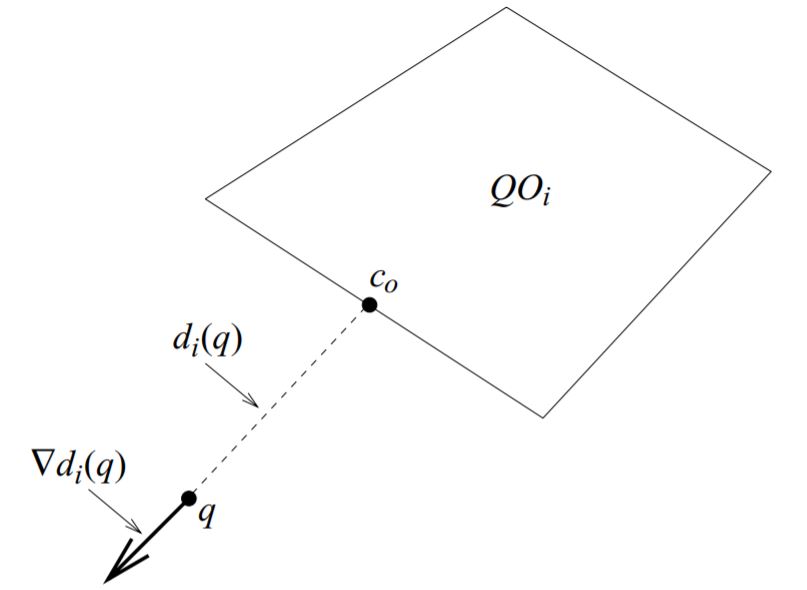
\[d_i(q) = \min_{c \in \mathcal{QO}_i} d(q,c) \tag{4.6}\]

对于凸障碍物\(\mathcal{QO_i}\)，\(c\)是距离\(x\)最近的点，\(d_i(q)\)的梯度为

\[\nabla d_i(q) = \frac{q-c}{d(q,c)} \tag{4.7}\]

向量\(\nabla d_i(q)\)描述了能够最大地增加\(\mathcal{QO_i}\)和\(q\)之间距离的方向（如图4.6所示）。

这样，每个障碍物都有自己的势函数

\[U_{rep_i}(q) = \begin{cases} \frac{1}{2} \eta \left( \frac{1}{d_i(q)} - \frac{1}{\mathcal{Q}_i^*} \right) \quad & , \text{if } d_i(q) \le \mathcal{Q}_i^* \\ 0 \quad & , \text{if } d_i(q) \gt \mathcal{Q}_i^* \\ \end{cases}\]

其中，\(\mathcal{Q}_i^*\)定义了障碍\(\mathcal{QO_i}\)作用域的大小。那么\(U_{rep}(q) = \sum_{i=1}{n} U_{rep_i}(q)\)。如果只有凸障碍或能分解成凸块的非凸障碍，就不会发生振荡，因为规划器在最近的点处不会发生突变。

4.2 Gradient Descent

梯度下降法是解决优化问题的著名方法。梯度下降算法如algorithm 4所示。

\(q(i)\)表示第i次迭代后\(q\)的值，最终的路径由迭代序列\({q(0),q(1),\ldots,q(i)}\)构成。标量\(\alpha(i)\)的值决定了第i次迭代的步长。\(\alpha(i)\)的值不能过大，否则机器人会"跳进"障碍物；也不能过小，否则会花费过多时间。在运动规划问题中，\(\alpha(i)\)的取值通常是特设的或者根据经验选取的。在优化书籍中有很多系统的选取方法。最后一点，梯度为零的情况很难准确达到，一般用\(\parallel \nabla U(q(i)) \lt \epsilon \parallel\)替代。

4.3 Computing Distance for Implementation in the Plane

本节讨论如何构造吸引/排斥势函数。如果机器人当前位置和目标位置均已知，那么吸引势函数很简单。难度主要在于排斥势函数的计算，因为需要计算与障碍物的距离。本节介绍了两种计算距离及对应势函数的方法。第一种方法利用基于传感器的移动机器人来实现，借用第2章中通过传感器推断距离的思想。第二种方法假设构型空间被离散成像素栅格，并在栅格上计算距离。

4.3.1 Mobile Robot Implementation

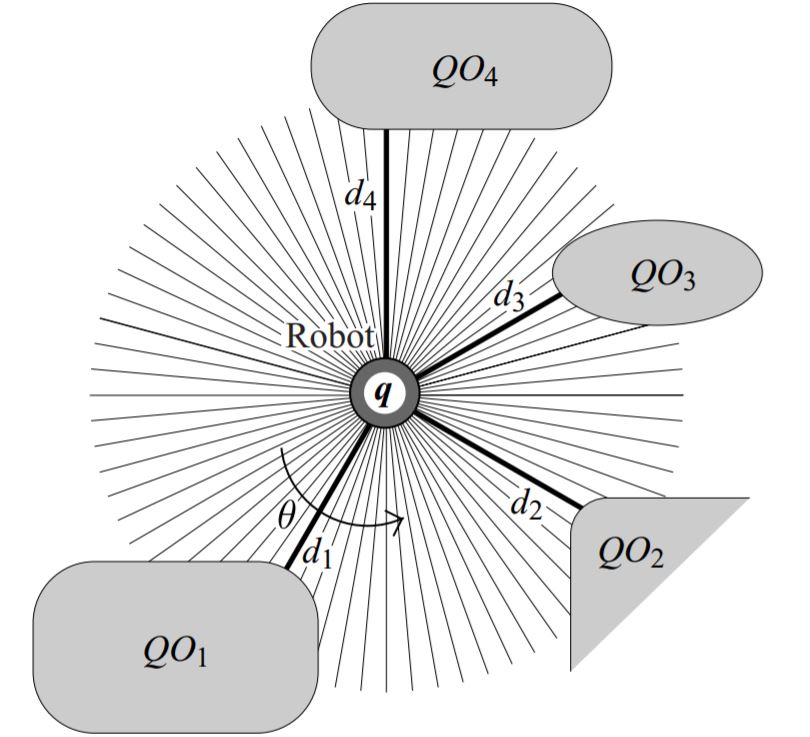
迄今为止，所有的讨论对于能够定义距离的构型空间具有一般性。考虑如图4.7所示的平面移动机器人，它装有放射状分布的距离传感器。这些距离传感器给出第2章中定义的原始距离函数\(\rho\)的近似。然而\(D(q)\)对应初始距离函数\(\rho\)的全局最小值，\(d_i(q)\)对应\(\rho(q,\theta)\)的局部最小值。比如，传感器会面向它对应的障碍物的最近的点，所以这些传感器指向能最大程度地将机器人移到距离障碍物最近的地方的方向，i.e. \(-\nabla d_i(q)\)。距离梯度指向与之相反。当障碍被另一个部分闭塞时，障碍距离函数可能会发生错误。

4.3.2 Brushfire Algorithm: A Method to Compute Distance on a Grid

这部分会介绍通过用栅格地图来计算距离的方法，栅格是被称为像素的二维正方形元素数组。当像素内完全没有障碍物的时候，其值为0；当像素完全或部分被障碍物占据时，其值为1。

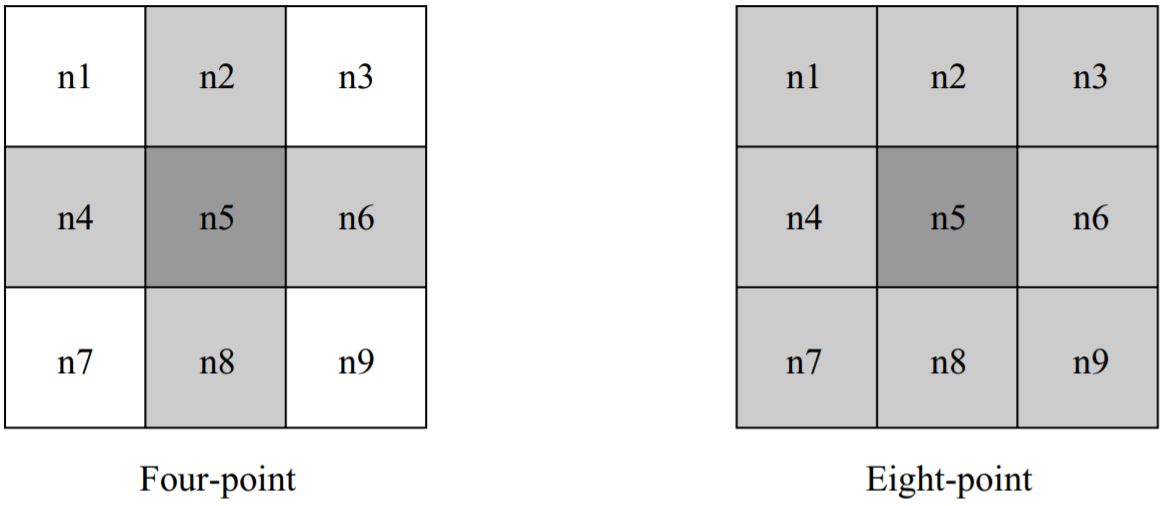
用户或规划器在决定像素在栅格中的邻居关系时有如图4.8所示两种选择。四点连接的好处是它遵循Manhattan距离函数（\(L_1\)度量）。

Brushfire算法利用栅格来近似距离和势函数。算法的输入是空为0障碍物为1的像素栅格，输出为值为与最近的障碍物的距离的像素栅格。这些值后面可以用来计算排斥势和梯度。

第一步：把所有与1值像素相邻的0值像素标记为2。然后，把所有和2邻接的0值像素标记为3。重复这个步骤，i.e. 所有和i相邻的0值像素都被标记为i+1，就像有森林大火从障碍物向外蔓延直到占据了所有自由像素。算法在所有像素都有指定值后停止（图4.9）。

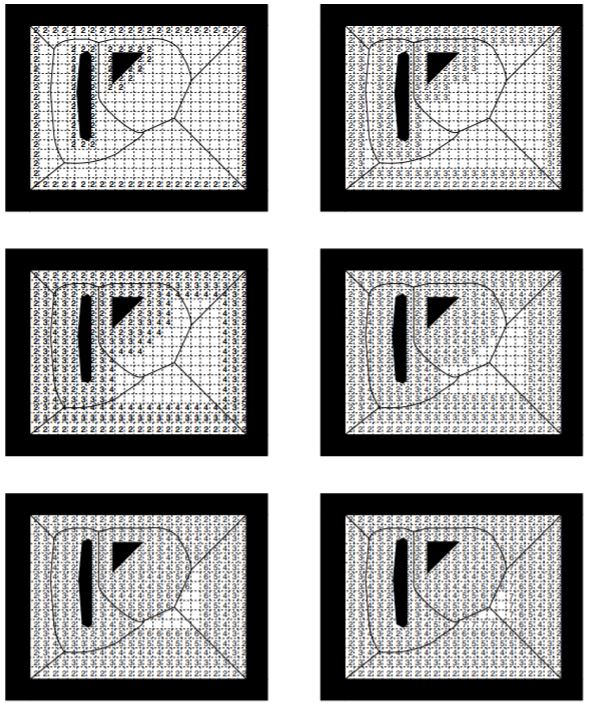
Fig 4.9 八点连接的brushfire算法的传播。实线穿过前面会碰撞的像素。

Brushfire算法生成了一张标注了与障碍物最近距离的地图。像素的距离梯度是指向值最小的邻居的向量。栅格是工作空间的一种近似，所以计算出的梯度也是实际距离梯度的近似。

得到与最近障碍物的距离和梯度后，规划器可以计算出排斥函数。吸引势函数可以通过解析计算，与排斥势函数一起，规划器可以用第一节中介绍的附加吸引/排斥函数。

值得注意的是，这个方法是可以推广到更高维的，只要选择合适的邻接关系，然后按上面描述的去迭代。这样尽管可行，在更高维用brushfire计算上还是很难的。

4.4 Local Minima Problem

所有的梯度下降算法都有一个共通的问题：势场中可能存在局部极值。梯度下降法一般可以保证能收敛到场的一个极小值，但无法保证这个极小值是全局极小值，即无法保证能到达目标点。图4.10是机器人被卡在凹型障碍物中的情形。除了凹障碍物，还有其他情况会产生这种问题，如图4.11所示。局部极小值是吸引、排斥法的严重缺陷，所以该方法不完全。

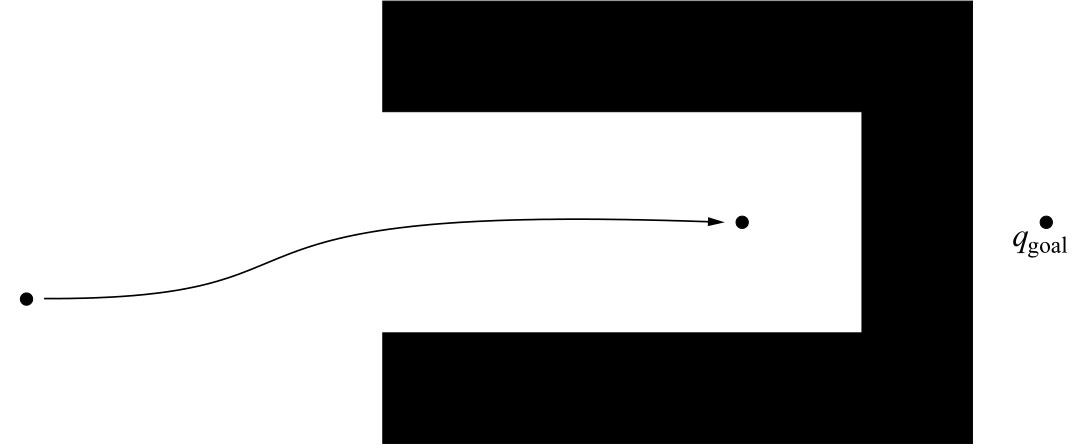
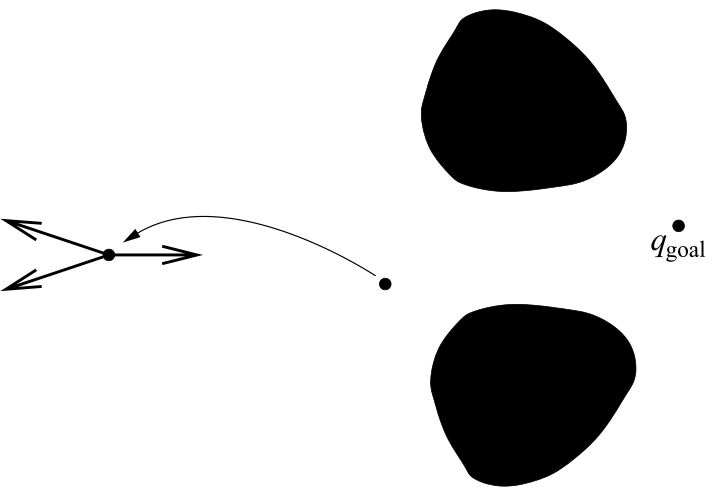
Fig 4.10 局部极小值在凹面内。机器人会一直向凹面移动，直到排斥梯度抵消吸引梯度。

Barraquand和Latombe提出了搜索的方法来克服利用势函数规划时的局部极小值问题，名为Randomized Path Planner (RPP)。
  

4.5 Wave-Front Planner

波前规划器提供了局部极小值问题的最简单的解决，但是只能用于可栅格化的空间。为了讨论方便，以二维空间为例。初始化时，规划器从标准的二进制网格开始，起点和目标点位置已知，目标点标记为2。首先，所有与目标相邻的0值像素标记为3。其次，所有与3邻接的标记为4。这个过程本质上每次迭代都生成了一个从目标出发的波前，波前上所有的像素到目标的路径长度相等。该步骤在波前到达起点所在像素的时候停止。

然后，规划器通过从起点出发的梯度下降确定出一条路径。本质上，规划器一次只决定一个像素的路径。自由空间的可靠性（其离散化也一样）和距离函数的连续性确保波前的构造能保证总是有比当前像素值少1的相邻像素，保证了这个步骤可以生成到达目标的路径。

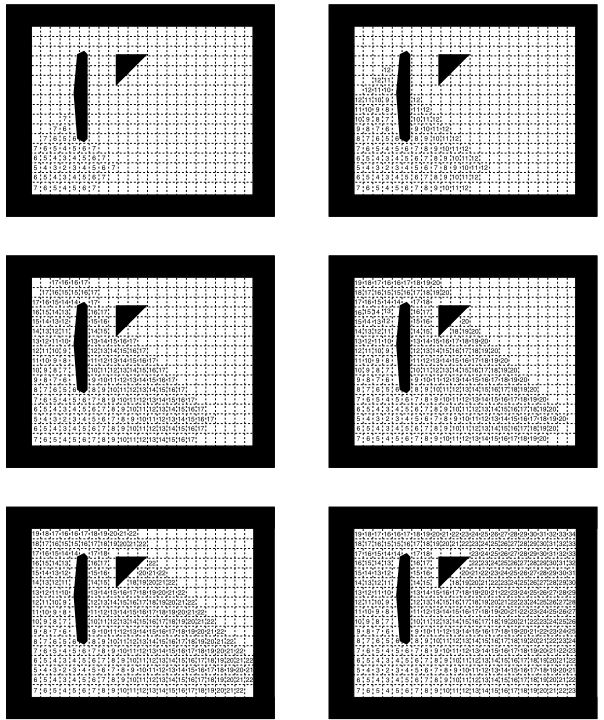
图4.12是以四点邻接的波前传播的不同阶段。波前上的所有点到目标的曼哈顿距离相同。左下角的图中，波前似乎要碰撞了，后面会发现这个初始碰撞点是距离函数的一个鞍点。这个点也从一开始就传播开来。传播的回溯与一组点相关，有两种最短的回到起点的路径，从三角形的上面或者下面。

波前规划器本质上生成了一个有一个局部极小值的基于栅格的势函数，所以它的解是完全的。此规划器可以找到最短路径，但是会离障碍物很近。此方法的主要缺陷就是需要搜索整个空间。

最终，和brushfire算法一样，波前规划器也可以拓展到更高维，但是计算会很麻烦。

先前在第2章中，bug算法是未知环境下完全基于传感器的规划器，但是只能在平面构型空间使用。而在本章的开始，吸引/排斥势函数可以应用于很多不同类型的构型空间，但是存在局部极小值的问题，并因此不完全。波前规划器解决了局部极小值问题，但是需要时间和关于空间纬度呈指数上升的存储。本节将介绍一种新的势，只有一个最小值且只能适用于一种构型空间（二维、三维或更多）的表示与障碍物距离的函数。这种势函数被称为navigation function。

DEFINITION 4.6.4 函数\(\phi : \mathcal{Q}_{free} \rightarrow [0,1]\)被称为navigation function，如果满足以下条件：

平滑（或至少\(C^k \text{ for } k \ge 2\)）
仅在\(q_{goal}\)处有唯一最小值，自由空间是相连的且包含\(q_{goal}\)
在自由空间的边界均匀地取到最大值
Morse

Morse函数的临界点都是非退化的。这意味着临界点都是孤立的，所以Morse函数用于梯度下降时，任意随机扰动就会破坏鞍点和最大值点的稳定性。在导航函数法中，将障碍物表示成\(\mathcal{QO}_i = \{ q \vert \beta_i(q) \le 0 \}\)，也就是说\(\beta_i(q)\)在\(\mathcal{QO}_i\)的内部为负，在\(\mathcal{QO}_i\)的边界为零，在\(\mathcal{QO}_i\)的外部为正。

4.6.1 Sphere-Space

此方法初始假设构型空间的边界为一个球心位于\(q_0\)的球体，且有\(n\)个位于\(q_1,q_2,\ldots,q_n\)的障碍物。障碍物距离函数定义为

\[\begin{aligned} \beta_0(q) & = -d^2(q,q_0) + r_0^2 \\ \beta_i(q) & = d^2(q,q_i) - r_i^2 \end{aligned}\]

其中，\(r_i\)为球体半径。此方法不再考虑到最近障碍物的距离或到各独立障碍物的距离，而是考虑其总和

\[\beta(q) = \sum_{i=0}^n {\beta_i(q)} \tag{4.8}\]

\(\beta(q)\)在任意障碍物的边界上为零，在自由空间内部的各个点处均为正。这就假设了各个障碍物是不相交的。

此方法用\(\beta\)构成类似排斥函数，导航函数的吸引部分为到目标距离的力，i.e.

\[\gamma_{\kappa}(q) = (d(q,q_{goal}))^{2 \kappa} \tag{4.9}\]

其中，\(\gamma_{\kappa}\)在目标处为零且当\(q\)远离目标时连续增长。函数\(\frac{\gamma_{\kappa}}{\beta}(q)\)仅在目标处为零，当\(q\)到达任一障碍物边界时趋向无穷。更重要的是，对于足够大的\(\kappa\)，函数\(\frac{\gamma_{\kappa}}{\beta}(q)\)有唯一的极小值。从本质上讲，增大\(\kappa\)会使\(\frac{\gamma_{\kappa}}{\beta}\)呈现以目标为中心的深碗的形式。同时，会让其他临界点被吸引向障碍物，因为障碍物的排斥作用范围相对吸引场的影响变小了。

在障碍物附近，只有障碍物有较大的影响。因此，局部极小值只可能出现在目标和障碍物之间的径向线上。在这条线靠近障碍物的边界处，\(\frac{\gamma_{\kappa}}{\beta}\)的Hessian不可能正定，因为当从障碍向目标移动时，\(\frac{\gamma_{\kappa}}{\beta}\)的值下降很快。因此对于足够大的\(\kappa\)，不存在除目标以外的极小值。

尽管\(\frac{\gamma_{\kappa}}{\beta}\)有唯一的极小值，但是它的值也会很大，难以计算。因此，引入分析开关，定义为

\[\sigma_{\lambda}(x) = \frac {x} {\lambda + x},\quad \lambda \gt 0 \tag{4.10}\]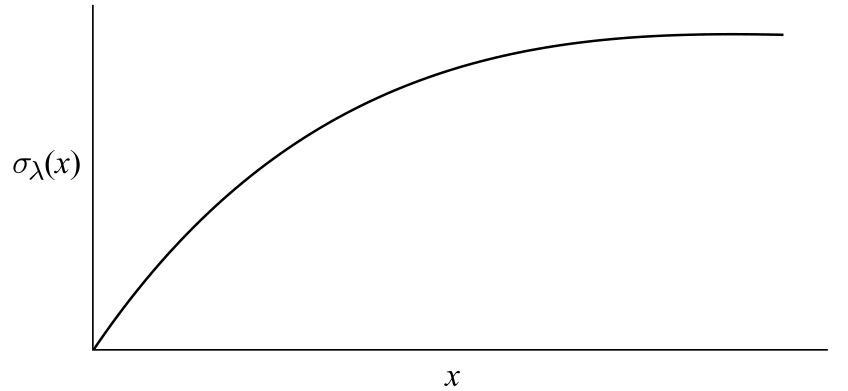

由于\(\sigma_{\lambda}(x)\)在\(x=0\)处为0，在\(x\)趋向于\(\infty\)时收敛到1，并且是连续的（图4.13），可以利用\(\sigma_{\lambda}(x)\)来约束函数\(\frac{\gamma_{\kappa}}{\beta}\)的值，i.e.

\[s(q,\lambda) = \left( \sigma_{\lambda} \circ \frac{\gamma_{\kappa}}{\beta} \right) (q) = \left( \frac{\gamma_{\kappa}} {\lambda \beta + \gamma_{\kappa}} \right) (q) \tag{4.11}\]

函数\(s(q,\lambda)\)在目标处值为零，在任意障碍的边界上有单一值，在自由空间内连续，并且对于足够大的\(\kappa\)有唯一的极小值。尽管如此，它还不一定是Morse函数，因为它可能有退化的临界点。所以，下面介绍另一个函数，它可以锐化\(s(q,\lambda)\)使其临界点为非退化的，i.e.，这样\(s(q,\lambda)\)就可以变为Morse函数。此函数为

\[\xi_{\kappa}(x) = x^{\frac{1}{\kappa}} \tag{4.12}\]

对于\(\lambda = 1\)，对应的在球形世界的导航函数为

\[\phi(q) = \left( \xi_{\kappa} \circ \sigma_1 \circ \frac{\gamma_{\kappa}}{\beta} \right) (q) = \frac {d^2 (q,q_{goal})} {[(d(q,q_{goal}))^{2\kappa} + \beta (q)]^{1 / \kappa}} \tag{4.13}\]

在\(\kappa\)取有效大的数时，此函数只在\(q_{goal}\)处有唯一的最小值。

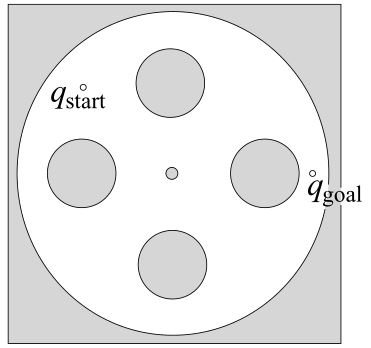
考虑如图4.14所示的构型空间。\(\kappa\)增大的效果如图4.15（\(\phi\)的等高线图）所示。

Fig 4.15 κ=3,κ=4,κ=6,κ=7,κ=8和κ=10对应的导航函数

Fig 4.16 κ=3,κ=4,κ=6,κ=7,κ=8和κ=10对应的导航函数

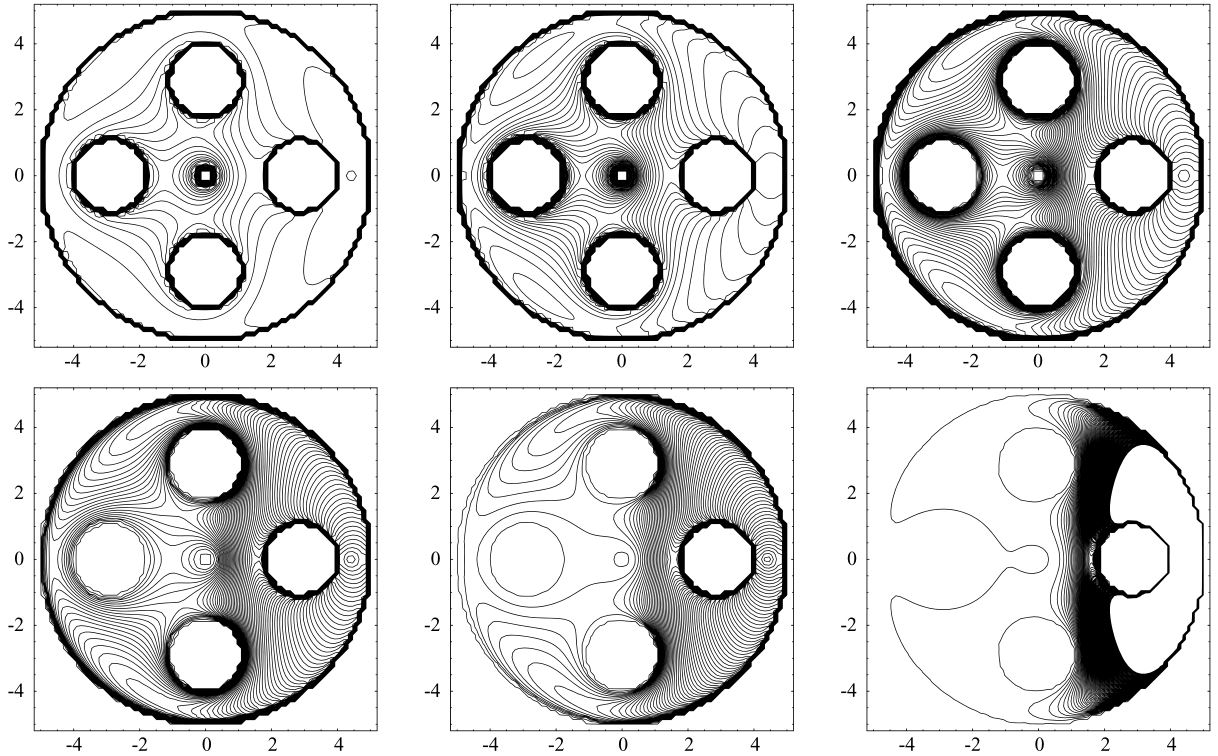
从图4.16中可以看到势函数变陡峭、临界点受目标点吸引和局部极值变为鞍点的过程。不幸的是，这种变陡的处理会使得导航函数在靠近目标和离目标较远时过于平坦，在两者之间时变化又很陡峭。这很容易使梯度下降方法出现数值误差。

4.6.2 Star-Space

球形空间的结果只是通往更具一般性的规划器的第一步。有了能在球形空间使用的导航函数，就可以找到和它微分同胚的其它构型空间的导航函数。

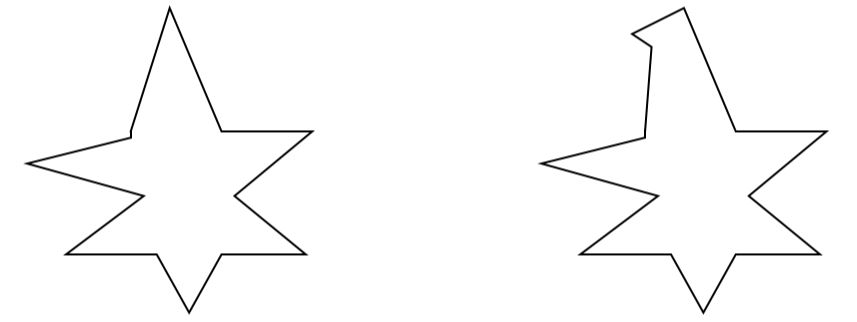
这个部分将会讨论由星形的构型空间和障碍物组成的星形空间。星形集\(S\)至少有一个点在其它所有集合中点的视线范围内，i.e. \(\exists x \text{ such that } \forall y \in S,\quad tx+(1-t)y \in S \quad \forall t \in [0,1]\)。如图4.17所示。所有凸集都是星形的，但反过来不成立。

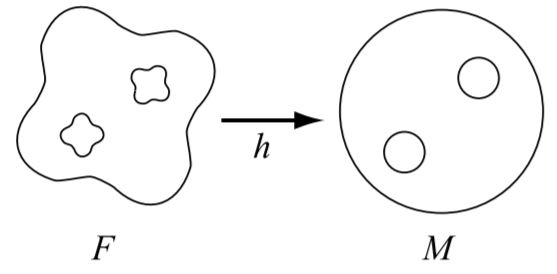
对于两个自由构型空间\(M\)和\(F\)，如果\(\phi : M \rightarrow [0,1]\)是\(M\)上的一个导航函数，并且存在映射\(h : F \rightarrow M\)为微分同胚映射，i.e. 此映射是平滑的、双射的且有平滑的反函数，那么\(\Phi = \phi \circ h\)为\(F\)上的导航函数（如图4.18所示）。微分同胚映射可以保证临界点是一一对应的。

构造星形和球形空间之间的映射\(h\)，可以利用缩放映射

\[T_i(q) = \nu _i(q) (q-q_i) + p_i \tag{4.14}\]

其中

\[\nu_i(q) = (1+\beta_i(q))^{1/2} \frac{r_i}{d(q,q_i)} \tag{4.15}\]

其中，\(q_i\)为星形集的中心，\(p_i\)和\(r_i\)分别为球形障碍物的中心和半径。这里由\(\beta_i(q)\)定义的星形集在内部为负，边界处为零，外部为正。

注意：若\(q_i\)在星形障碍物的边界上，那么\((1+\beta_i(q))=1\)，因此\(T_i = r_i \frac{q-q_i}{d(q,q_i)} + p_i\)。也就是说，\(T_i(q)\)将星形集边界上的点映射为了一个球。

对于星形障碍物\(QO_i\)，定义分析开关

\[s_i(q,\lambda) = \left( \sigma_{\lambda} \circ \frac{ \gamma_{\kappa} \bar{\beta}_i }{ \beta_i } \right) (q) = \left( \frac{ \gamma_{\kappa} \bar{\beta}_i }{\gamma_{\kappa} \bar{\beta}_i + \lambda \beta_i } \right) (q) \tag{4.16}\]

其中，

\[\bar{\beta}_i = \prod_{j = 0, j \neq i}^{n} \beta_j \tag{4.17}\]

i.e. \(\bar{\beta}_i\)在除了当前障碍物\(QO_i\)外的障碍物边界上为零。注意：\(s_i(q,\lambda)\)在\(QO_i\)的边界上为1，但在目标和除\(QO_i\)外障碍物的边界上为0。

为目标也定义一个类似的开关函数，令其在目标处为1，在自由空间的边界处为0，i.e.

\[s_{q_{goal}} (q,\lambda) = 1 - \sum_{i=0}^{M} s_i \tag.{4.18}\]

现在，利用以上函数和转换的缩放映射，就可以定义一个星形空间和球形空间之间的映射为

\[h_{\lambda}(q) = s_{q_{goal}} (q,\lambda) T_{q_{goal}}(q) + \sum_{i=0}^{M} s_i(q,\lambda) T_i(q) \tag{4.19}\]

其中，\(T_{q_{goal}}(q)=q\)为恒等映射，是为了符号一致性。

注意：在\(QO_i\)的边界上时，\(h_{\lambda}(q)\)即为\(T_i(q)\)，因为\(s_i\)在\(QO_i\)的边界上对所有的\(j \neq i\)均为1，\(s_j\)在\(QO_i\)的边界上均为0（这里将\(s_{q_{goal}}\)视为\(s_j\)之一）。也就是说，对于任意的\(s_i\)，在障碍物\(QO_i\)的边界上时\(h_{\lambda}(q)\)即为\(T_i(q)\)，将星形的边界映射到球形上。进一步地，\(h_{\lambda}(q)\)是连续的，因此可以将成功星形空间映射到球形空间。可以看出，对于一个合适的\(\lambda\)，\(h_{\lambda}(q)\)是平滑、双射且有平滑的反函数的，i.e. 为微分同胚映射。因此，当得到球形空间的导航函数后，就可以得到星形空间的导航函数。

4.7 Potential Functions in Non-Euclidean Spaces

暂且搁置局部极小的问题，完成势函数的另一个挑战就是第一步的构建构型空间。当构型空间是非欧几里得且多维的时候，这步尤为困难。要解决这个问题，需要先定义在欧几里得的工作空间内的势函数，然后把它转移到构型空间中。这里，我们计算构型空间中的梯度作为工作空间中梯度的函数。如果要这么做，我们现在要将梯度视为力，而不是之前的速度矢量。然后，就可以将这个关系运用到单一的刚体机器人上。最后，将这个关系用到multibody机器人上。本节的讨论集中在4.1节中的吸引、排斥势上。

4.7.1 Relationship between Forces in the Workspace and Configuration Space

由于工作空间是低维空间的一个子集（\(\mathbb{R}^2\)或\(\mathbb{R}^2\)），所以在工作空间内实现和评估势函数比在构型空间内容易得多。将工作空间的梯度看作是力，工作空间的势函数自然会影响工作空间的力，但最终还是需要构型空间内的力来决定最终的机器人路径。

用坐标向量\(x\)和\(q\)分别表示工作空间内的点和机器人的构型，其中坐标\(x\)和\(q\)根据前向运动学（第三章）相关\(x=\Phi(q)\)。用\(f\)和\(u\)分别表示工作空间和构型空间中的广义力。根据虚功原理，功（或功率）是与坐标无关的量，所以两个空间内的功一定是相等的。在工作空间内，力\(f\)所做的功为\(f^T \dot{x}\)。在构型空间内，功为\(u^T \dot{q}\)。由第3章3.8节可知\(\dot{x} = J \dot{q}\)，其中\(J = \partial \Phi / \partial q\)为前向运动学映射的Jacobian。因此，工作空间的力到构型空间的力的映射为

\[\begin{aligned} f^T J \dot{q} &= u^T \dot{q} \\ f^T J &= u^T \\ J^T f &= u . \\ \end{aligned}\]