Duality & Sensitivity Analysis

4.1 Dual Linear Program

4.1.1 Introduction

  给定一个constraint matrix \(\mathbf{A}\)、right hand side vector \(\mathbf{b}\)和cost vector \(\mathbf{c}\)，可以得到一个对应的线性规划问题（原始问题）

\[\text{(LP)} \quad \begin{aligned} \text{min} \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} = \mathbf{b} \\ & \mathbf{x} \ge 0 \end{aligned}\]

问：1. 可以用同样的数据\((\mathbf{A, b, c})\)来构建另一个线性规划问题嘛？
  2. 如果是这样，这个新的线性规划与原来的原始问题有什么关系？

猜想：\(\mathbf{A}\)是一个\(m \times n\)的矩阵，\(\mathbf{b}\)是一个\(m\)维向量，\(\mathbf{c}\)是一个\(n\)维向量。
  \(\mathbf{b}\)和\(\mathbf{c}\)的角色可以互换吗？
  如果是这样，我们将会得到\(m\)个变量和\(n\)个约束。相应地，
   （1）应该考虑将矩阵\(\mathbf{A}\)转置，将行改为列，反之亦然?
   （2）非负变量→自由变量？
   （3）等式约束→不等式约束？
   （4）最小化目标函数→最大化目标函数？

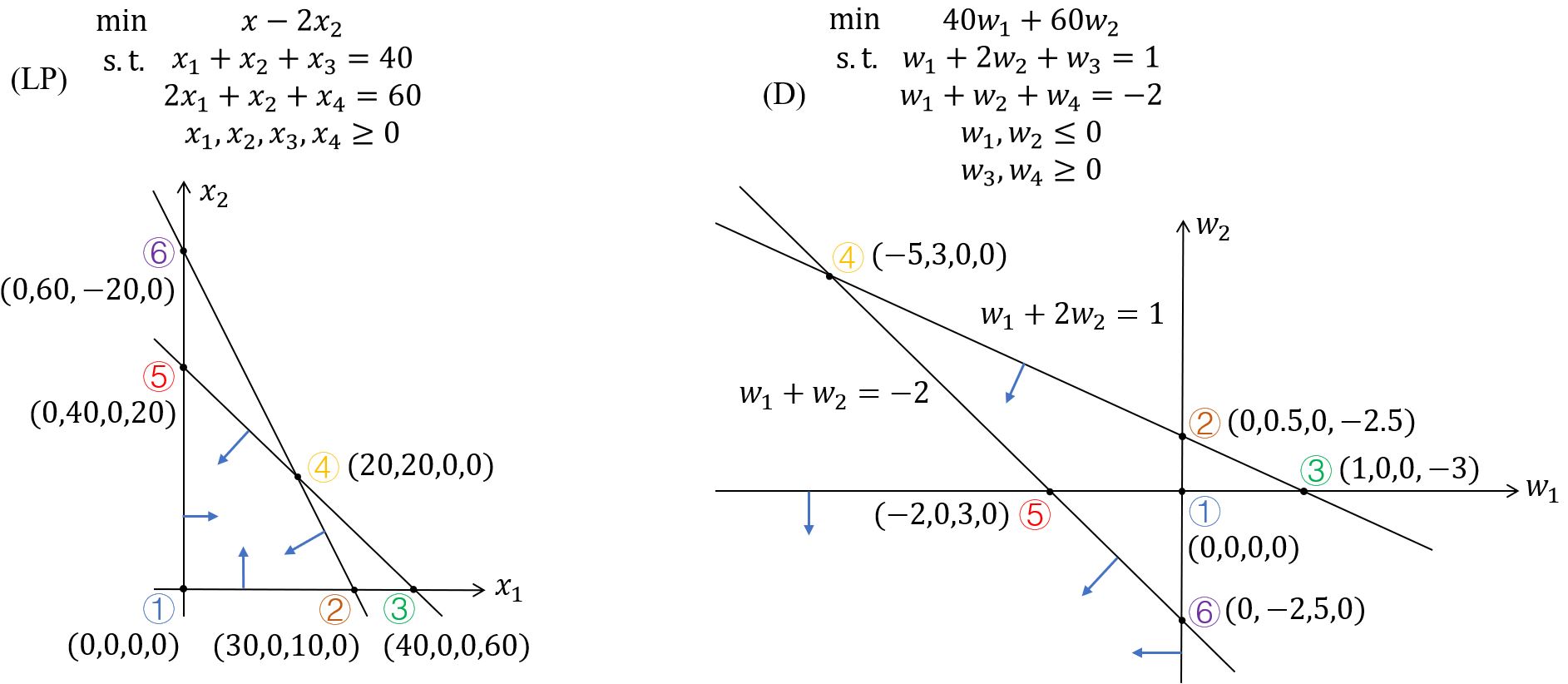
Dual linear program
  考虑如下线性规划

\[\color{green}{ \text{(D)} \quad \begin{aligned} \text{max} \quad & \mathbf{b}^T \mathbf{w} \\ \text{s.t.} \quad & \mathbf{A}^T \mathbf{w} \le \mathbf{c} \quad \text{Dual Problem} \\ & \mathbf{w} \in \mathbb{R}^m \end{aligned} }\]

原来的线性规划为

\[\text{(LP)} \quad \begin{aligned} \text{min} \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} = \mathbf{b} \quad \text{Primal Problem} \\ & \mathbf{x} \ge 0 \end{aligned}\]

例

4.1.3 Dual of LP in other form

Symmetric pair

\[\text{(P)} \quad \begin{aligned} \min \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} \ge \mathbf{b}\\ & \mathbf{x} \ge 0 \end{aligned} \qquad \qquad \qquad \text{(D)} \quad \begin{aligned} \max \quad & \mathbf{b}^T \mathbf{w} \\ \text{s.t.} \quad & \mathbf{A}^T \mathbf{w} \le \mathbf{c} \\ & \mathbf{w} \ge 0 \end{aligned}\] \[\qquad \qquad \quad \begin{aligned} \min \quad & \mathbf{c}^T \mathbf{x} + \mathbf{0}^T \mathbf{s} \\ \text{s.t.} \quad & \mathbf{Ax-Is} = \mathbf{b}\\ & \mathbf{x, s} \ge 0 \end{aligned} \qquad \qquad \quad \quad \begin{aligned} \max \quad & \mathbf{b}^T \mathbf{w} \\ \text{s.t.} \quad & \begin{bmatrix} \mathbf{A}^T \\ - \mathbf{I} \end{bmatrix} \mathbf{w} \le \begin{bmatrix} \mathbf{c} \\ \mathbf{0} \end{bmatrix} \end{aligned}\]

Karmarkar's form LP

\[\begin{aligned} \min \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n}=0 \\ & \qquad \qquad \qquad \vdots \\ & a_{m 1} x_{1}+a_{m 2} x_{2}+\cdots+a_{m n} x_{n}=0 \\ & x_{1} + x_{2} + \cdots + x_{n} = 1 \\ & x_{1}, x_{2}, \ldots, x_{n} \geq 0\\ \end{aligned} \qquad \qquad \text{(DKLP)} \begin{aligned} \max \quad & w_{m+1} \\ \text{s.t.} \quad & a_{11} u_{1}+\cdots+a_{m 1} w_{m}+w_{m+1} \leq c_{1}\\ & a_{12} w_{1}+\cdots+a_{m 2} w_{m}+w_{m+1} \leq c_{2}\\ & \qquad \qquad \qquad \quad \vdots \\ & a_{1 n} w_{1}+\cdots+a_{m n} w_{m}+w_{m+1} \leq c_{n} \end{aligned}\]

Dual (KLP)总是可行的，比如：
  \(w_1 = w_2 = \cdots = w_m = 0\)，\(w_{m+1} = \min \{ c_1, c_2, \ldots, c_n \}\)，那么这个\(\mathbf{w} = [w_1, \ldots, w_m, w_{m+1}]^T\)对于DKLP就是可行的。

4.2 Duality Theory

问：LP和它的对偶问题是怎么联系起来的呢？

我们用(P) primal problem表示原来的LP，用(D) dual problem表示新的新的LP。
(P)和(D)是用一样的数据\((\mathbf{A, b, c})\)定义的
(D)问题是一个有\(m\)个变量、\(n\)个约束的线性规划问题，右端向量和成本向量在(P)和(D)中的角色互换了。

还有什么呢？

4.2.1 Dual relationship

  如果把(D)看作primal problem，会发生什么？

\[\begin{aligned} \text{max} \quad & \mathbf{b}^T \mathbf{w} \\ \text{s.t.} \quad & \mathbf{A}^T \mathbf{w} \le \mathbf{c}\\ & \mathbf{w} \in \mathbb{R}^m \end{aligned}\]

  通过以下几步将(D)写成它的标准型： (1) 令\(\mathbf{w = u - v}\)； (2) 增加松弛变量\(s\)； (3) 最小化目标函数。

\[\text{(P)} \quad \begin{aligned} \min \quad & \begin{bmatrix} -\mathbf{b}^T & \mathbf{b}^T & 0 \end{bmatrix} \begin{bmatrix} \mathbf{u} \\ \mathbf{v} \\ \mathbf{s} \end{bmatrix} \\ \text{s.t.} \quad & \begin{bmatrix} \mathbf{A}^T & -\mathbf{A}^T & \mathbf{I} \end{bmatrix} \begin{bmatrix} \mathbf{u} \\ \mathbf{v} \\ \mathbf{s} \end{bmatrix} = \mathbf{c} \\ & \mathbf{u, v, s} \ge 0 \end{aligned} \qquad \qquad \qquad \text{(D)} \quad \begin{aligned} \max \quad & \mathbf{c}^T \mathbf{w} \\ \text{s.t.} \quad & \begin{bmatrix} \mathbf{A} \\ -\mathbf{A} \\ \mathbf{I} \end{bmatrix} \mathbf{w} \le \begin{bmatrix} -\mathbf{b} \\ \mathbf{b} & 0 \end{bmatrix}\\ & \mathbf{w} \text{ unrestricted } \in \mathbb{R}^n \end{aligned}\]

Lemma 4.1：Dual of the dual = primal

  整理新得到的对偶问题，有\(\begin{aligned} -\max \quad & \mathbf{c}^T \mathbf{w} \\ \text{s.t.} \quad & \mathbf{Aw} \le -\mathbf{b}\\ & -\mathbf{Aw} \le \mathbf{b} \\ & \mathbf{w} \le 0 \end{aligned}\)，即\(\begin{aligned} \text{min} \quad & -\mathbf{c}^T \mathbf{w} \\ \text{s.t.} \quad & -\mathbf{Aw} = \mathbf{b}\\ & \mathbf{w} \le 0 \end{aligned}\)。对于\(\mathbf{x} := - \mathbf{w}\)，我们有\(\begin{aligned} \min \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} = \mathbf{b}\\ & \mathbf{x} \ge 0 \end{aligned}\)。

4.2.2 Weak duality theorem

  如果\(\mathbf{x}\)是(P)的一个可行解，\(\mathbf{w}\)是(D)的一个可行解，那么\(\begin{aligned} \mathbf{c}^T \mathbf{x} & =\mathbf{x}^T \mathbf{c} \\ & \ge \mathbf{x}^T \mathbf{A}^T \mathbf{w} \\ & = \mathbf{b}^T \mathbf{w} \end{aligned}\)

Weak Duality Theorem：如果\(\mathbf{x}\)是(P)的一个原始可行解，\(\mathbf{w}\)是(D)的一个对偶可行解，那么\(\mathbf{c}^T \mathbf{x} \ge \mathbf{b}^T \mathbf{w}\)。

Corollaries：

1. 如果\(\mathbf{x}\) primal feasible，\(\mathbf{w}\) dual feasible，且\(\mathbf{c}^T \mathbf{x} = \mathbf{b}^T \mathbf{w}\)，那么\(\mathbf{x}\)是primal optimal，\(\mathbf{w}\)是dual optimal。
2. 如果原始问题是无下界的，那么它的对偶问题无解。（反之成立吗？）
3. 如果对偶问题是无上界的，那么它的原始问题无解。（反之成立吗？）

4.2.3 Strong duality theorem

问：weak duality的结果可以再强一些吗？
  原始最优值与对偶最优值之间是否还有一些距离?

Strong Duality Theorem：
  （1）如果原始问题和对偶问题中任一个存在有限的最优值，那么另一个也有，并且\(\min \mathbf{c}^T \mathbf{x} = \max \mathbf{b}^T \mathbf{w}\)。（No duality gap!）
  （2）如果任一个问题的目标值无界，那么另一个问题无解。

证：（1）注意到对偶的对偶是原始问题，并且还有一个事实"如果\(\mathbf{x}\) primal feasible，\(\mathbf{w}\) dual feasible，且\(\mathbf{c}^T \mathbf{x} = \mathbf{b}^T \mathbf{w}\)，那么\(\mathbf{x}\)是primal optimal，\(\mathbf{w}\)是dual optimal"。我们只需要证明这一点：如果原始问题有一个有限的最优bfs \(\mathbf{x}\)，那么就存在一个对偶可行解\(\mathbf{w}\)使得\(\mathbf{c}^T \mathbf{x} = \mathbf{b}^T \mathbf{w}\)。

  对最优bfs \(\mathbf{x}\)用单纯形法，其基为\(\mathbf{B}\)，定义：\(\mathbf{w}^T = \mathbf{c}_B^T \mathbf{B}^{-1}\)。那么

\[\begin{aligned} \mathbf{c}-\mathbf{A}^{T} \mathbf{w} &= \left[ \begin{array}{c} \mathbf{c}_{B} \\ \mathbf{c}_{N} \end{array}\right] -\left[ \begin{array}{c} \mathbf{B}^{T} \\ \mathbf{N}^{T} \end{array}\right] \mathbf{w} \\ &= \left[ \begin{array}{c} \mathbf{c}_{B}-\mathbf{B}^{T}\left(\mathbf{B}^{T}\right)^{-1} \mathbf{c}_{B} \\ \mathbf{c}_{N}-\mathbf{N}^{T}\left(\mathbf{B}^{T}\right)^{-1} \mathbf{c}_{B} \end{array}\right] \\ &= \left[ \begin{array}{c} 0 \\ r_{N} \end{array}\right] \geq 0 \end{aligned}\]

因此\(\mathbf{w}\) dual feasible，且

\[\begin{aligned} \mathbf{c}^{T} \mathbf{x} &=\mathbf{c}_{B}^{T} \mathbf{x}_{B} \\ &= \mathbf{c}_{B}^{T} \mathbf{B}^{-1} \mathbf{b} \\ &= \mathbf{w}^{T} \mathbf{b} \\ &= \mathbf{b}^{T} \mathbf{w} \end{aligned}\]

  （2）这可以直接由弱对偶定理得到。

Implications：

1. Simplex multiplier \(\color{green}{\mathbf{w}}\)与原始最优解\(\mathbf{x}\)对应，是一个对偶最优解。
2. 在单纯形法的每次迭代过程中simplex multiplier \(\mathbf{w}\)始终满足\(\mathbf{c}^T \mathbf{x} = \mathbf{b}^T \mathbf{w}\)。但是，只有当\(r_N \ge 0\)时\(\mathbf{w}\)是对偶可行的。
3. Revised simplex method：在保证原始问题可行和\(\mathbf{c}^T \mathbf{x} = \mathbf{b}^T \mathbf{w}\)（no duality gap）的同时，寻求对偶可行性。（在原始问题到达最优前无法得到\(r_N \ge 0\)。）

Further implications of strong duality theorem

Theorem of Alternatives：不等式系统解的存在性

Farkas Lemma：系统\(\mathbf{Ax = b}, \mathbf{x} \ge 0\)无解，当且仅当\(\mathbf{A}^T \mathbf{w} \le 0, \mathbf{b}^T \mathbf{w} \ge 0\)。
另一种形式：有两个系统，(Ⅰ)\(\mathbf{Ax = b}, \mathbf{x} \ge 0\)，(Ⅱ)\(\mathbf{A}^T \mathbf{w} \le 0, \mathbf{b}^T \mathbf{w} \ge 0\)，这两个系统有且只有一个有解。

证：考虑LP和对应的dual

\[\text{(P)} \quad \begin{aligned} \min \quad & \mathbf{0}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} = \mathbf{b}\\ & \mathbf{x} \ge 0 \end{aligned} \qquad \qquad \qquad \text{(D)} \quad \begin{aligned} \max \quad & \mathbf{b}^T \mathbf{w} \\ \text{s.t.} \quad & \mathbf{A}^T \mathbf{w} \le \mathbf{0} \end{aligned}\]

  因为\(\mathbf{w = 0}\)是对偶可行的，可知当且仅当(D)是无下界时(P)不可行。注意当且仅当(Ⅰ)无解时(P)不可行，当且仅当(Ⅱ)有解(D)无上界。因此，当且仅当(Ⅱ)有解时(Ⅰ)无解。

4.2.4 Complementary slackness

  考虑symmetric pair LP

\[\text{(P)} \quad \begin{aligned} \min \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} \ge \mathbf{b}\\ & \mathbf{x} \ge 0 \end{aligned} \qquad \qquad \qquad \text{(D)} \quad \begin{aligned} \max \quad & \mathbf{b}^T \mathbf{w} \\ \text{s.t.} \quad & \mathbf{A}^T \mathbf{w} \le \mathbf{c} \\ & \mathbf{w} \ge 0 \end{aligned}\]

令\(\mathbf{x}\) primal feasible，\(\mathbf{w}\) dual feasible，定义

\[\color{green}{\begin{aligned} \mathbf{s} & = \mathbf{Ax - b} \ge 0 \\ \mathbf{r} & = \mathbf{c - A}^T \mathbf{w} \ge 0 \end{aligned}}\]

其中，\(\mathbf{s} \in \mathbb{R}^m\)为primal slackness，\(\mathbf{r} \in \mathbb{R}^n\)为dual slackness。

Observations：
  1. 如果\(\begin{cases} \mathbf{r}^T \mathbf{x} = 0 \\ \mathbf{w}^T \mathbf{s} = 0 \end{cases}\)（complementary slackness，互补松弛条件），那么有\((\mathbf{c}^{T}-\mathbf{w}^{T} \mathbf{A}) \mathbf{x}=0\)和\(\mathbf{w}^T (\mathbf{Ax = b}) = 0\)，所以，\(\mathbf{c}^T \mathbf{x} = \mathbf{w}^T \mathbf{Ax} = \mathbf{w}^{T} \mathbf{b} = \mathbf{b}^T \mathbf{w}\)。因此\(\mathbf{x}\) primal feasible，\(\mathbf{w}\) dual feasible。
  2. 相反，对于一对可行的\((\mathbf{x, w})\)，有\(\mathbf{c}^T \mathbf{x} \ge \mathbf{w}^T \mathbf{Ax} \ge \mathbf{b}^T \mathbf{w}\)。如果\(\mathbf{x}\) primal feasible，\(\mathbf{w}\) dual feasible，那么\(\mathbf{c}^T \mathbf{x} = \mathbf{w}^T \mathbf{Ax} = \mathbf{w}^{T} \mathbf{b}\)。因此有\((\mathbf{c}^{T}-\mathbf{w}^{T} \mathbf{A}) \mathbf{x}=0\)和\(\mathbf{w}^T (\mathbf{Ax = b}) = 0\)。

Complementary slackness theorem：令(P)和(D)为一对"symmetric pair"，\(\mathbf{x}\) primal feasible，\(\mathbf{w}\) dual feasible，那么\(\mathbf{x}\)和\(\mathbf{w}\)为一对最优解，当且仅当\(\begin{cases} r_{j}=0 \text { or } x_{j}=0 \quad \forall j=1,2, \ldots, n \\s_{i}=0 \text { or } w_{i}=0 \quad \forall i=1,2, \ldots, m \end{cases}\)。

标准LP的互补松弛条件

\[\text{(P)} \quad \begin{aligned} \min \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} = \mathbf{b}\\ & \mathbf{x} \ge 0 \end{aligned} \qquad \qquad \qquad \text{(D)} \quad \begin{aligned} \max \quad & \mathbf{b}^T \mathbf{w} \\ \text{s.t.} \quad & \mathbf{A}^T \mathbf{w} \le \mathbf{c} \end{aligned}\]

  条件\(\mathbf{w}^T \mathbf{s} = 0\)始终成立，所以互补松弛条件退化为\(\mathbf{r}^T \mathbf{x} = 0\)。

  进一步地，\(\text{gap} = \mathbf{c}^T \mathbf{x} - \mathbf{b}^T \mathbf{w} = \mathbf{c}^T \mathbf{x} - \mathbf{Ax}^T \mathbf{w} = \mathbf{x}^T \mathbf{c} - \mathbf{x}^T \mathbf{A}^T \mathbf{w} = \mathbf{x}^T \mathbf{r}\)。也就是说，gap = 0和互补松弛条件是等价的。

4.2.5 Kuhn-Tucker condition

Terorem：\(\mathbf{x}\)是问题\(\text{(P)} \ \begin{aligned} \min \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} = \mathbf{b}\\ & \mathbf{x} \ge 0 \end{aligned}\)的最优解，当且仅当存在\(\mathbf{w}\)和\(\mathbf{r}\)使得 \(\begin{aligned} &(1) \mathbf{A} \mathbf{x}=\mathbf{b},\mathbf{x} \geq 0 \\ &(2) \mathbf{A}^{T} \mathbf{w}+\mathbf{r}=\mathbf{c}, \mathbf{r} \geq 0 \\ &(3) \mathbf{r}^{T} \mathbf{x}=0 \end{aligned} \begin{aligned} \text{ (Primal feasibilty)} \\ \text{ (Dual feasibilty)} \\ \text{ (Complementary Slackness)} \end{aligned}\)。

Implication：解一个线性规划问题等价于解一个线性不等式系统。

4.2.6 Economic interpretation of duality

• 对偶变量有什么特殊的含义吗？
• 一个对偶问题要做什么？
• 互补松弛条件在决策中的作用是什么？

Dual variables

  考虑一个非退化的线性规划：

\[\text{(P)} \quad \begin{aligned} \min \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} = \mathbf{b} \\ & \mathbf{x} \ge 0 \end{aligned} \quad \begin{aligned} \text{ (minimize total cost)} \\ \text{ (satisfy demands)} \\ \text{ (different services)} \end{aligned}\]

  假设\(\mathbf{x}^{*}\)是非退化的最优bfs，\(\mathbf{x}^{*}=\begin{bmatrix} \mathbf{x}_{B}^{*} \\ 0 \end{bmatrix} = \begin{bmatrix} \mathbf{B}^{-1} \mathbf{b} \\ 0 \end{bmatrix}\)，\(z^{*} = \mathbf{c}^T \mathbf{x}^{*} = \mathbf{c}_B^T \mathbf{B}^{-1} \mathbf{b}\)。因为\(\mathbf{x}_B^{*} = \mathbf{B}^{-1} \mathbf{b} \ge 0\)，所以当\(\Delta \mathbf{b}\)足够小时\(\mathbf{B}^{-1} = (\mathbf{b} + \Delta \mathbf{b})\)。那么\(\bar{\mathbf{x}}^{*}=\begin{bmatrix} \mathbf{x}_{B}^{*} \\ 0 \end{bmatrix} = \begin{bmatrix} \mathbf{B}^{-1} = (\mathbf{b} + \Delta \mathbf{b}) \\ 0 \end{bmatrix}\)是\((\bar{\text{P}}) \ \begin{aligned} \min \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} = \mathbf{b} + \Delta \mathbf{b} \\ & \mathbf{x} \ge 0 \end{aligned}\)的一个最优bfs，且\(\bar{z}^{*} = \mathbf{c}_B^T \mathbf{B}^{-1} (\mathbf{b} + \Delta \mathbf{b})\)。（Why? 因为\(\mathbf{r}_q没变！\)）

  进一步地，我们有\(\Delta z = \bar{z}^{*} - z^{*} = \mathbf{c}_B^T \mathbf{B}^{-1} (\mathbf{b} + \Delta \mathbf{b}) - \mathbf{c}_B^T \mathbf{B}^{-1} \mathbf{b} = \mathbf{c}_B^T \mathbf{B}^{-1} \Delta \mathbf{b}\)。（这里的\(\mathbf{c}_B^T \mathbf{B}^{-1} = \mathbf{w}^T\)即为(P)最优时的simplex multiplier!）

  因此，\(w_i\)就是第\(i\)个需求的"marginal price"。注意：对偶变量\(w_i\)表示对额外需求\(i\)所收取的最低单价，也称shadow price或equilibrium price。

Dual LP problem

考虑以下生产场景：

• 要生产\(n\)种产品，\(x_j =\)产品\(j\)的数量，\(j = 1, 2, \ldots, n\)
• 有\(m\)种原料，\(b_i\)是原料\(i\)的数量，\(i = 1, 2, \ldots, m\)
• 每种产品的市场售价已知为\(c_1, c_2, \ldots, c_n\)
• technology matrix：\(a_{ij}\)为每个产品\(j\)消耗的原料\(i\)的数量

从制造商的角度:

• 最大化总销量（即利润）\(\sum_{j=1}^n c_j x_j\)
• 原料限制\(a_{i1}x_1 + a_{i2}x_2 + \ldots + a_{in}x_n \le b_i, i = 1, 2, \ldots, m\)
• 产品要求\(x_i \ge 0, j = 1, 2, \ldots, n\)

\[\text{(P)} \quad \begin{aligned} \max \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} \le \mathbf{b} \\ & \mathbf{x} \ge 0 \end{aligned}\]

获取原料：

• 从供应商处买\(m\)种原料，\(w_i\) = 购买原料\(i\)的单价，\(i = 1, 2, \ldots, m\)
• 自由信息市场：供应商知道产品\(x_j\)的售价\(c_j\)，并且他/她希望从我的身上赚更多，i.e. \(a_{1j}w_1 + a_{2j}w_2 + \ldots + a_{mj}w_m \ge c_j, j = 1, 2, \ldots, n\)

因此，可以得到对偶问题

\[\begin{aligned} \min \quad & \mathbf{b}^T \mathbf{w} \\ \text{s.t.} \quad & \mathbf{A}^T \mathbf{w} \ge \mathbf{c} \\ & \mathbf{w} \ge 0 \end{aligned} \quad \begin{aligned} \text{（最小总花费）} \\ \text{（供应商能接受的价格）} \\ \quad \end{aligned}\]

互补松弛条件：
 1. \(w_i^*\)是生产者愿意付给原料商买原料\(i\)的最大原料价格
 2. 当原料\(i\)没有全被用完时，i.e. \(a_{i1}x_1^* + a_{i2}x_2^* + \ldots + a_{in}x_n^* \lt b_i\)，互补松弛条件意味着\(w_i^* = 0\)。也就是说，制造商不愿意为购买任何额外的数量支付一分钱!
 3. 当供应商要价太多时，i.e. \(a_{1j}w_1 + a_{2j}w_2 + \ldots + a_{mj}w_m \gt c_j\)，那么\(x_j = 0\)。也就是说，这意味着制造商不会生产任何产品\(j\)！

4.3 Sensitivity Analysis

4.4 Dual Simplex Method