Proximal Policy Optimization

  PP是OpenAI默认的强化学习算法。

2.1 Review on PG

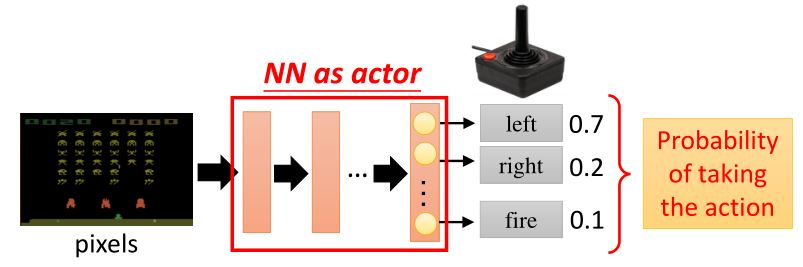
策略\(\pi\)是一个关于参数\(\theta\)的网络

• 输入：机器所观察到的内容，表示成一个向量或矩阵
• 输出：每个动作对应于输出层的一个神经元

\[\text{轨迹 }\tau = \{ s_1, a_1, s_2, a_2, \cdots, s_T, a_T \}\] \[\begin{aligned} p_{\theta}(\tau) &= p\left(s_{1}\right) p_{\theta}\left(a_{1} \mid s_{1}\right) p\left(s_{2} \mid s_{1}, a_{1}\right) p_{\theta}\left(a_{2} \mid s_{2}\right) p\left(s_{3} \mid s_{2}, a_{2}\right) \cdots \\ &= p\left(s_{1}\right) \prod_{t=1}^{T} p_{\theta} \left(a_{t} \mid s_{t}\right) p\left(s_{t+1} \mid s_{t}, a_{t}\right) \end{aligned}\]

\[\text{expected reward } \bar{R}_{\theta} = \sum_{\tau} R(\tau) p_{\theta}(\tau) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [R(\tau)]\]

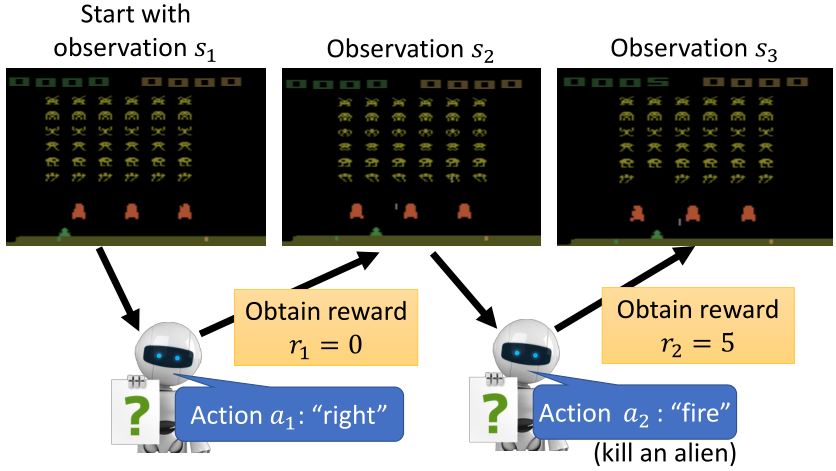
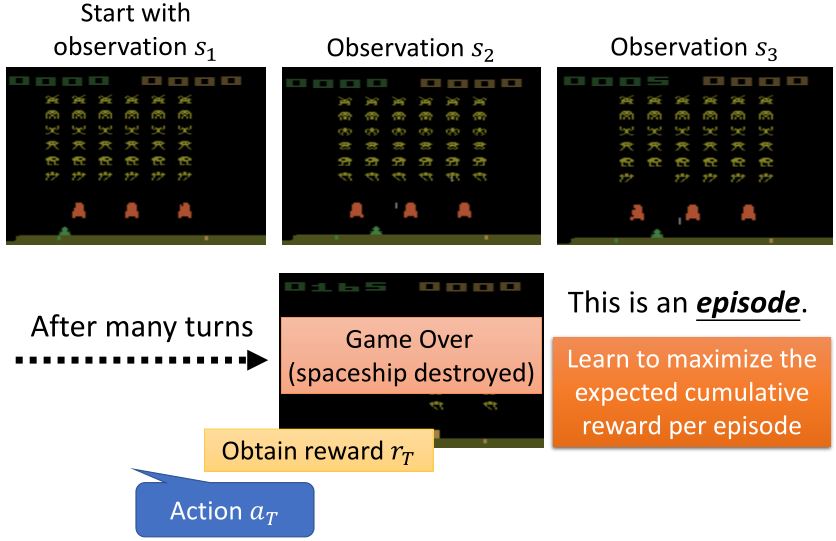
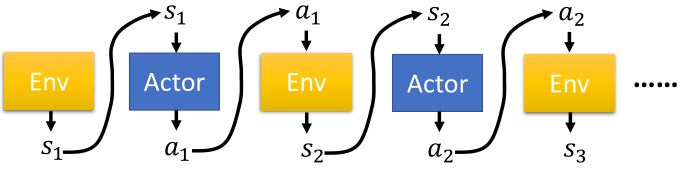
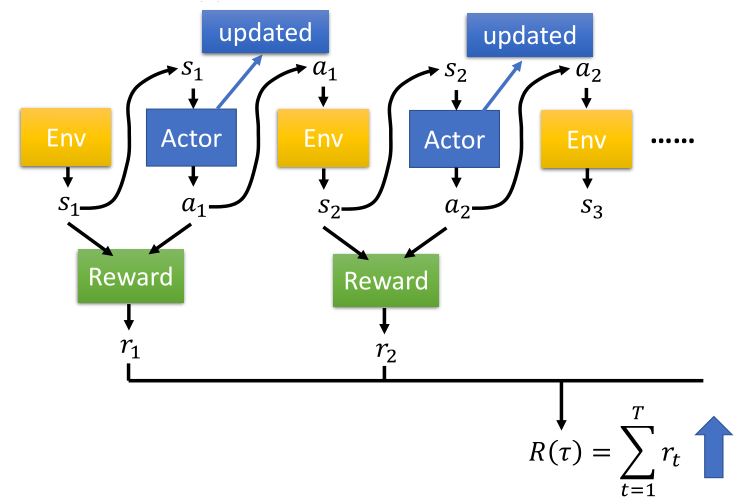
  要使期望奖励最大，利用梯度上升法来更新参数。

\[\begin{aligned} \text{policy gradient } \nabla \bar{R_{\theta}} =& \sum_{\tau} R_{\tau} \nabla p_{\theta}(\tau) = \sum_{\tau} R_{\tau} p_{\theta}(\tau) \nabla \log p_{\theta}(\tau) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [R_{\tau} \nabla \log p_{\theta}(\tau)] \\ \approx & \frac{1}{N} \sum_{n=1}^N R(\tau^n) \nabla \log p_{\theta}(\tau^n) = \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} R(\tau^n) \nabla \log p_{\theta}(a_{t}^n \mid s_{t}^n) \end{aligned}\]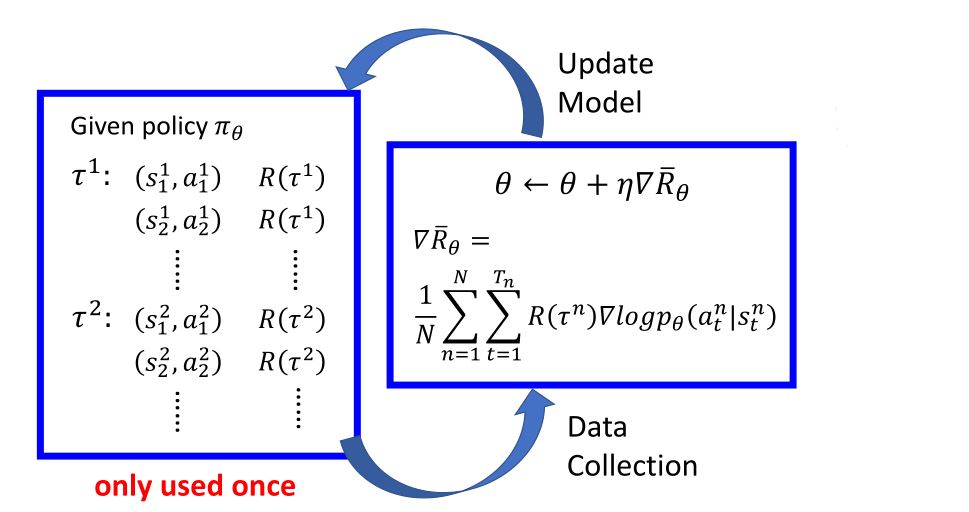

2.1.1 Implementation

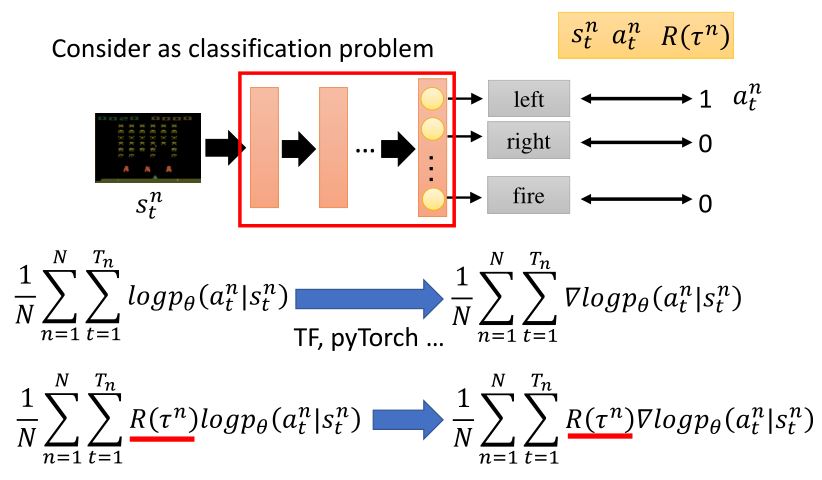
  如果从分类问题的角度看，将状态作为输入，每个行为看作是一个标签，那么输出就应该是每种类型对应的概率。可以看出，强化学习的过程相比于分类问题多了一个total reward。

2.1.2 Tips

1. Add a baseline

  可能存在\(R(\tau^n)\)一直为正的情况（e.g. 打乒乓球），所以需要减去一个\(b\)。

\[\begin{aligned} &\theta^{new} \leftarrow \theta^{old} + \eta \nabla \bar{R}_{\theta^{old}} \\ &\nabla \bar{R_{\theta}} \approx \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} \big(R(\tau^n) - b\big) \nabla \log p(a_{t}^n \mid s_{t}^n, \theta) \quad b \approx \mathbb{E}[R(\tau)] \end{aligned}\]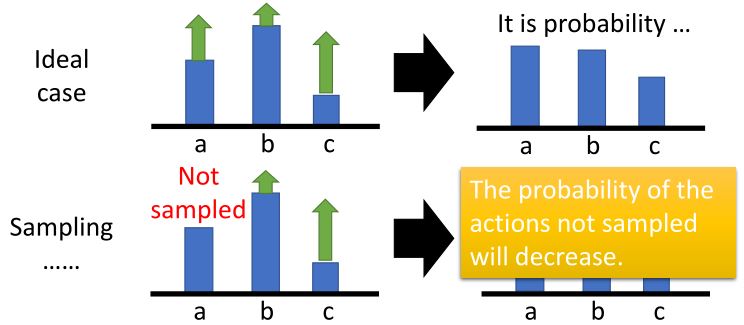

2. Assign suitable credit

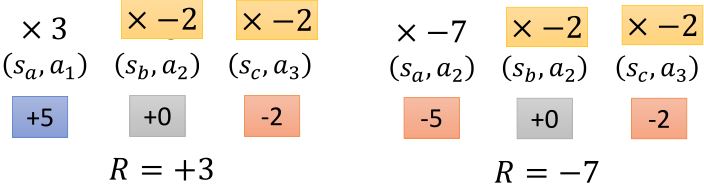
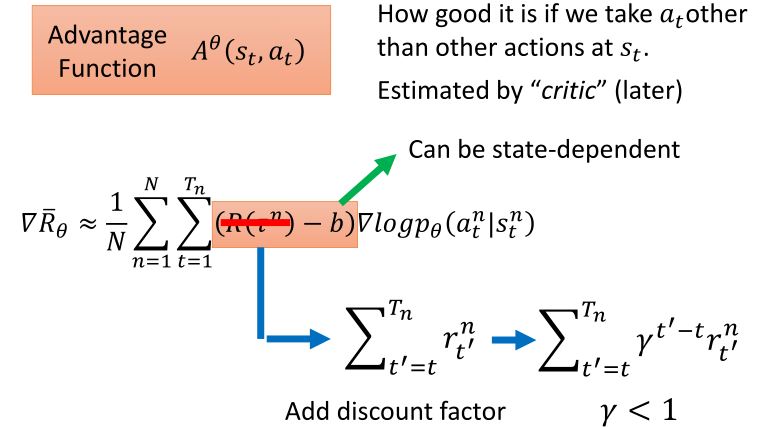
  在一个episode中，可能有好的action和不好的action，一个trajectory得到的total reward高并不能代表所有的action都很好。如果我们可以采样足够多次，那么就可以避免这个问题。但是，现在我们的采样次数有限，所以要给每个action一个credit，将total reward改为从某个行为被执行后累计的reward，并添加折扣因子。

2.2 On-policy → Off-policy

• On-policy：学习到的agent和与环境交互的agent是同一个
• Off-policy：学习到的agent和与环境交互的agent是不同的

\[\nabla \bar{R_{\theta}} = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [R_{\tau} \nabla \log p_{\theta}(\tau)]\]

• 用策略\(\pi_{\theta}\)收集数据，当\(\theta\)被更新时，必须要重新采样训练数据
• 目标：用从策略\(\pi_{\theta '}\)的采样来训练\(\theta\)。\(\theta '\)是固定的，所以其采样数据可以重用。

重要性采样

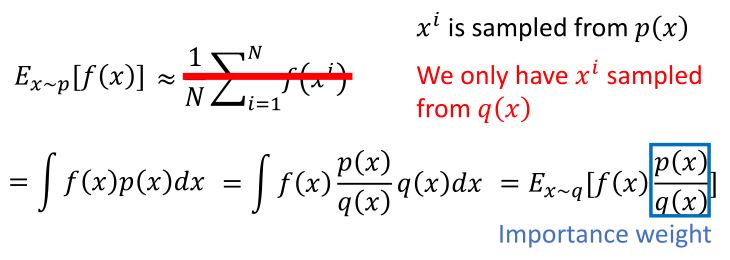
  理论上，两个概率分布的期望是一样的，但是方差不一样。所以要有足够多的样本，并且两个概率分布的差距不能太大。

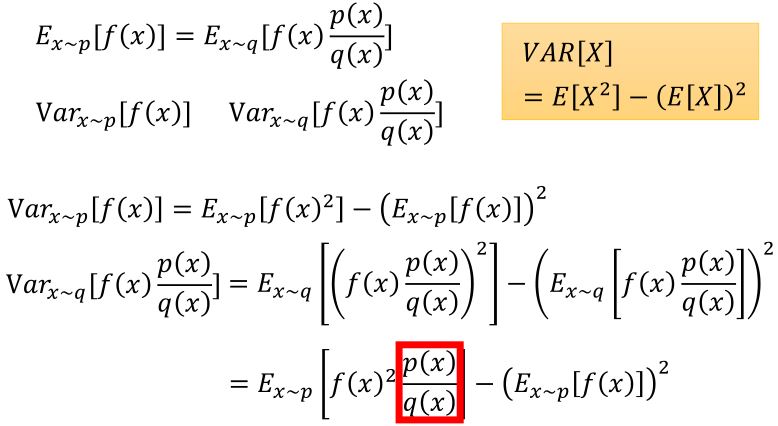
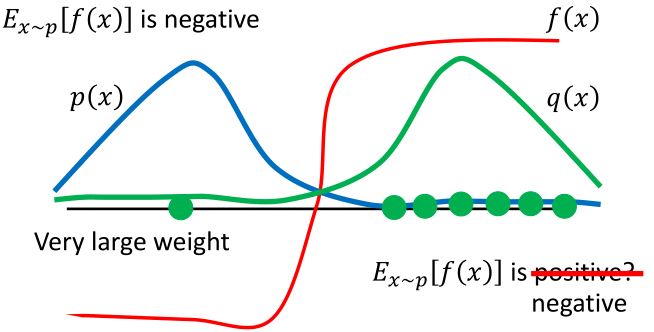
利用重要性采样，\(\nabla \bar{R}_{\theta} = E_{\tau \sim p_{\theta}(\tau)} \left[ R(\tau) \nabla \log p_{\theta}(\tau) \right] = E_{\tau \sim p_{\theta'}(\tau)} \left[ \frac{p_{\theta}(\tau)}{p_{\theta^{\prime}}(\tau)} R(\tau) \nabla \log p_{\theta}(\tau) \right]\)，从\(\theta '\)采样数据，多次训练\(\theta\)。

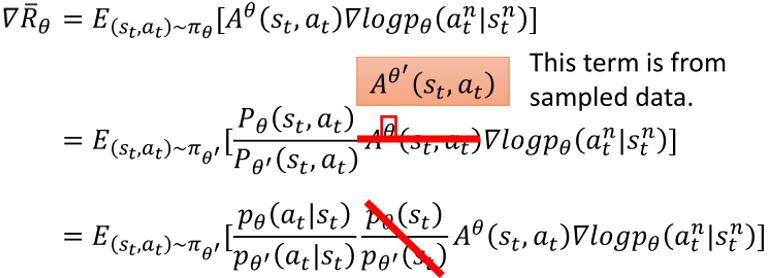
目标函数可以写成\(J^{\theta'}(\theta) = = E_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \frac{p_{\theta}(a_t \mid s_t)}{p_{\theta^{\prime}}(a_t \mid s_t)} A^{\theta'} (s_t, a_t) \right]\)

2.3 Add Constraint

  因为重要性采样要求两个概率分布的差距不能太大，在PPO (Proximal Policy Optimization)中增加了一个\(KL(\theta, \theta')\)的约束

\[\begin{aligned} J_{PPO}^{\theta'}(\theta) &= J^{\theta'}(\theta) - \beta KL(\theta, \theta') \\ J^{\theta'}(\theta) &= E_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \frac{p_{\theta}(a_t \mid s_t)}{p_{\theta^{\prime}}(a_t \mid s_t)} A^{\theta'} (s_t, a_t) \right] \end{aligned}\]

  在TRPO (Trust Region Policy Optimization)中，这个约束的位置和PPO不一样。两种方法的效果相差不大，但是PPO更容易实现。

\[J_{PPO}^{\theta'}(\theta) = E_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \frac{p_{\theta}(a_t \mid s_t)}{p_{\theta^{\prime}}(a_t \mid s_t)} A^{\theta'} (s_t, a_t) \right] \quad KL(\theta, \theta') \le \delta\]

2.3.1 PPO algorithm

• 初始化策略参数\(\theta^0\)
• 在每次迭代中
   用\(\theta^k\)和环境交互收集\(\{ s_t, a_t \}\)并计算advantage \(A^{\theta^k} (s_t, a_t)\)
   找出能最优化\(J_{PPO}(\theta)\)的\(\theta\)

2.3.2 PPO2 algorithm

\[J_{PPO2}^{\theta^{k}}(\theta) \approx \sum_{(s_{t}, a_{t})} \min \left( \frac{p_{\theta} (a_t \mid s_t)}{p_{\theta^k}\left(a_t \mid s_t\right)} A^{\theta^k}(s_t, a_t) , \operatorname{clip} \left(\frac{p_{\theta}\left(a_{t} \mid s_{t}\right)}{p_{\theta^{k}}\left(a_{t} \mid s_{t}\right)}, 1-\varepsilon, 1+\varepsilon\right) A^{\theta^k}(s_t, a_t) \right)\]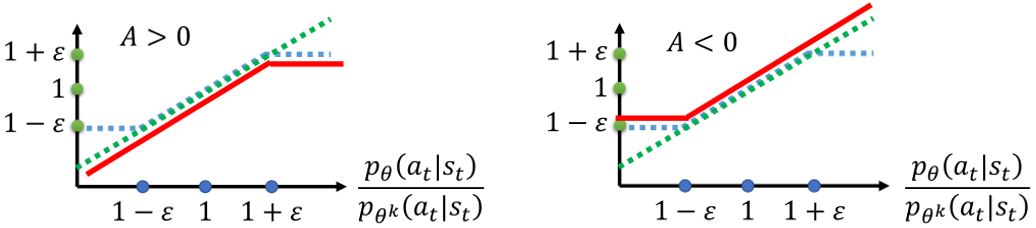

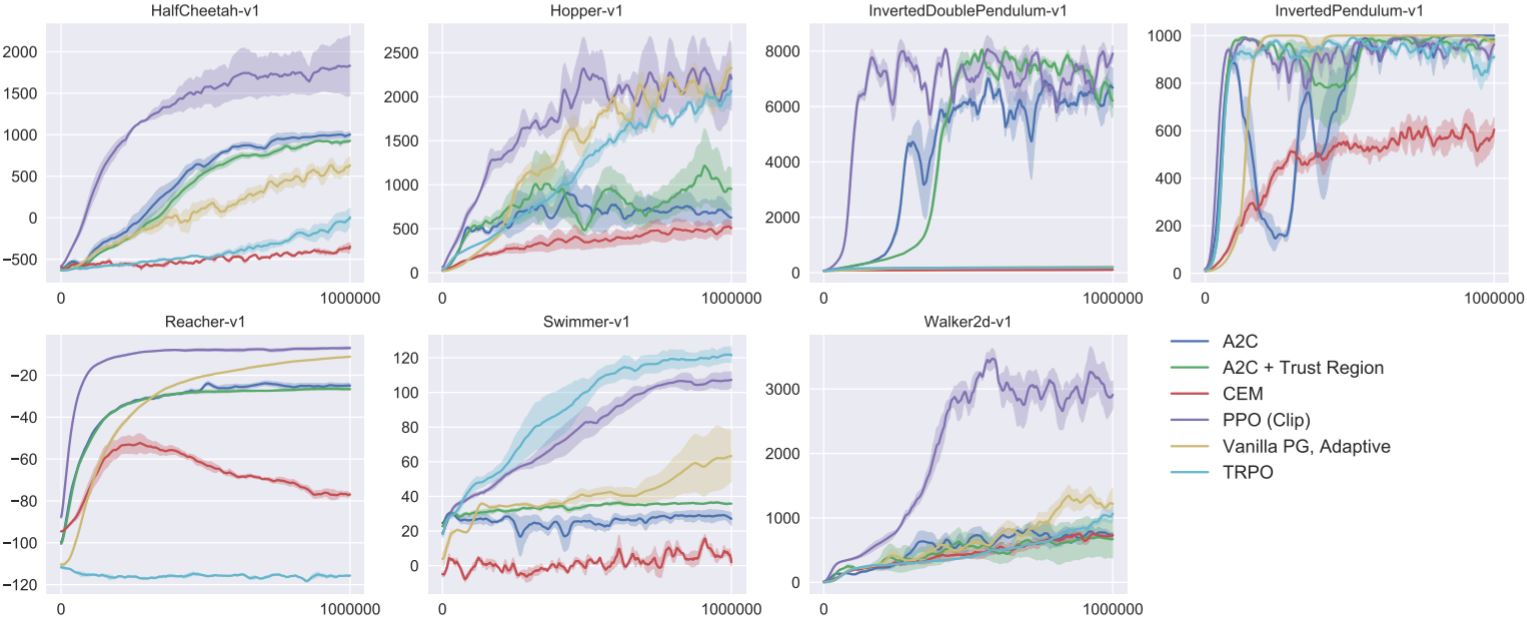
2.3.3 Experimental results

参考文献：Proximal Policy Optimization Algorithms