Roadmaps

  根据第2章和第4章的内容可知，规划器规划的是一条从某个指定开始构型到另一个指定结束构型的路径。如果在同一个环境中需要规划很多路径，那么就有必要构建一种数据结构来提高规划子路径的速度。这个数据结构就称为map，而根据传感器数据生成机器人环境模型的任务就称为mapping。在室内系统的背景下，三种地图概念占主导地位：拓扑、几何和栅格（如图5.1所示）。

Fig 5.1 表示环境的不同方法：拓扑、几何和运用栅格

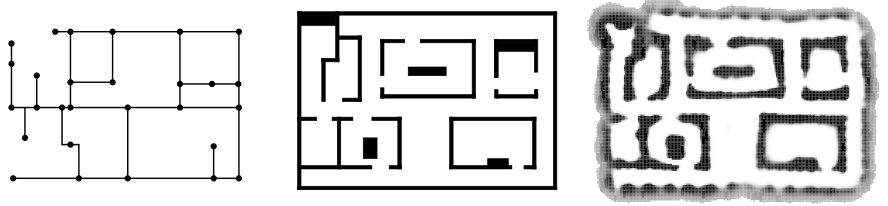
  拓扑表示主要用于表示具有图状结构的环境，在这种环境中，节点对应于"不同的东西"，边表示节点之间的邻接关系。最近用度量信息（e.g. 相对距离，角度）来增广拓扑地图变得流行起来，这也可以帮助区分"看"起来相同的地点或是可以利用这些信息来导航。
  几何模型使用几何图元来表示环境。然后，建图相当于估计基元的参数使其最适合于传感器的观察。几何模型有很多种不同的表示，很多学者使用线段来表示部分环境。目前比较流行的还有用三角形网格来表示环境的三维结构。
  占用栅格是栅格结构，类似于第 4 章中描述的那些，其中每个像素的值表示的是其对应工作空间或构型空间的部分被占用的可能性。

  本章着重介绍一种被称为roadmaps的拓扑地图。Roadmap嵌在自由空间中，因此roadmap的节点和边也具有物理意义。比如，一个roadmap的节点对应于某个指定地点，边对应于相邻地点间的路径。因此，除了作为图之外，roadmap还是一维流形的集合，用于捕获自由空间的显著拓扑。
  机器人使用roadmap的方式与人们使用高速公路系统的方式大致相同，大部分运动发生在高速公路系统上，这将驾驶者从起点附近带到目标附近。类似地，使用roadmap，规划器可以先在roadmap上找到一条无碰撞路径，穿越roadmap到目标附近，然后构造一个从路线图上的点到目标的无碰撞路径。大部分运动发生在roadmap上，因此无需在多维空间中进行搜索，不管这个多维空间是工作空间还是构型空间。

DEFINITION 5.0.2 (Roadmap) 一维曲线的联合是roadmap RM，如果对于所有\(\mathcal{Q}_{free}\)中可以被某条路径相连的\(q_{start}\)和\(q_{goal}\)，以下性质都存在的话：

  1. Accessibility：存在从\(q_{start} \in \mathcal{Q}_{free}\)到某个\(q'_{start} \in RM\)的路径，
  2. Departability：存在从某个\(q'_{goal} \in RM\)到\(q_{goal} \in \mathcal{Q}_{free}\)的路径，
  3. Connectivity：在RM中存在从\(q'_{start}\)到\(q'_{goal}\)的路径。

  本章将介绍5种roadmap：visibility maps, deformation retracts, retract-like structures, piecewise retracts and silhouettes。Visibility maps往往适用于具有多边形障碍的构型空间。Deformation retractions类似于融化的冰或燃烧的草地。用于silhouettes法的表示是通过将机器人的多维自由空间的阴影重复投影到低维空间来构建的，直到形成一维网络。

5.1 Visibility Maps

  Visibility map的定义特征是，如果节点在彼此的视线范围内，那么这些节点共享一条边，并且机器人自由空间中的所有点都在visibility map上至少一个节点的视线范围内。第二点意味着visibility map，根据定义，具有可访问性和可离开性。连通性是使得每个地图的结构成为roadmap所必须明确证明的一点。本节将考虑最简单的visibility map，称为visibility graph。

5.1.1 Visibility Graph Definition

  标准可视图是定义在一个二维多边形构型空间中的（图5.3）。可视图的节点\(v_i\)包含了起始未知、目标位置以及构型空间中障碍物的所有顶点。图的边\(e_{ij}\)是连接两个视线节点\(v_i\)和\(v_j\)的直线段，i.e. \(e_{ij} \neq \emptyset \ \Longleftrightarrow \ s v_i + (1-s)v_j \ \in \text{cl}(\mathcal{Q}_{\text{free}}) \ \forall s \in [0, 1]\)。

Fig 5.3 多边形构型空间、起点和目标

注意，我们将节点和边嵌入到自由空间中，并且多边形障碍物的边也视作可视图中的边。

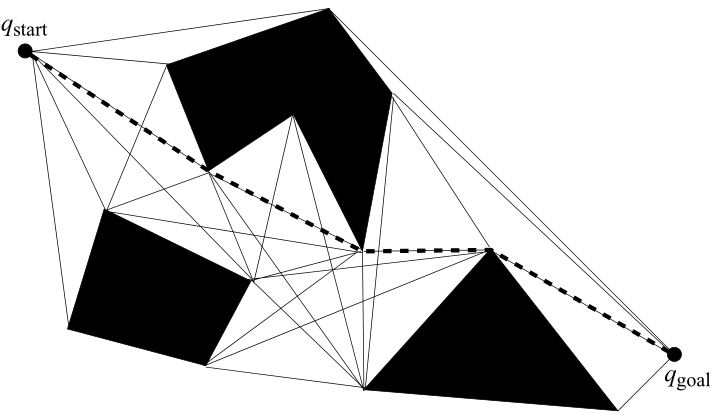
Fig 5.4 细实线描绘了填充了三个多边形障碍物的可视图的边。粗虚线表示起点和目标之间的最短路径。

  利用标准二范数（欧几里得距离），可以搜索可视图的最短路径（图5.4）。可视图的定义可以被推广到具有多面体障碍物的三维构型空间，但是不一定包含这样的空间中的最短路径。

  不幸的是，可视图有很多不必要的边。利用supporting和separating lines可以减少边的数量。