NeRF开山之作

NeRF: representing scenes as neural radiance fields for view synthesis

3.1 神经辐射场

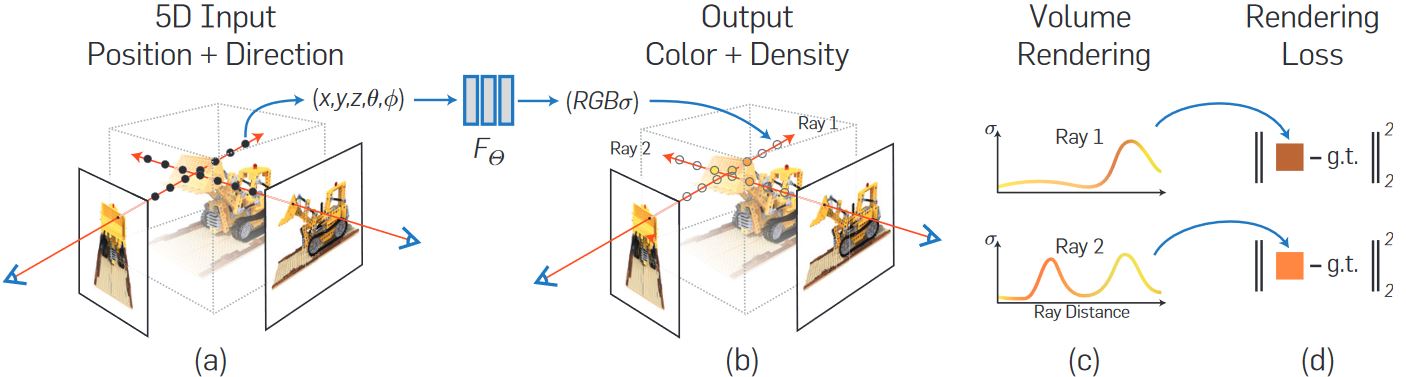
三维场景：坐标值\((x, y, z)\) + 体密度\(\sigma\)（与材质有关） + 观察角度\((\theta, \phi)\)看到的颜色值\(C\)（考虑了镜面反射问题）
辐射场：定义在空间中的函数，记录了空间中每个点的体密度𝜎以及该点每个方向上的颜色值\(C\)（辐射值）
体渲染：视线上所有的点投射到图像上形成像素颜色的过程
神经网络：全连接神经网络\(F_{\Theta}\)

NeRF的pipeline：

• 推断：输入视线上点的坐标\((x, y, z)\)和观察角度\((\theta, \phi)\)，神经网络输出对应的RGB值和体密度\(\sigma\)。这样对视线上的每个点进行计算，将得到的结果进行体渲染，完成图像的生成。
• 训练：计算生成的图像与真实图像之间的误差，完成神经网络的更新。

3.2 体渲染

3.2.1 视线

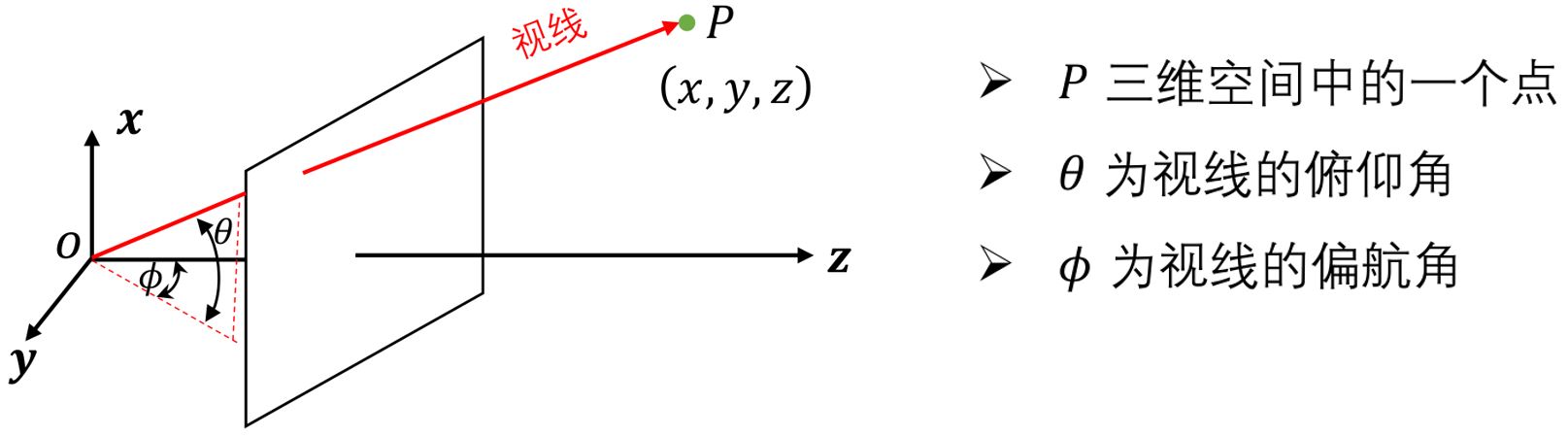
视线\(r\)上的点可以表示为：

\[\color{green}{\mathbf{r}(t) = \mathbf{o} + t \mathbf{d}}\]

其中，\(\mathbf{o}\)是摄像机的光心在世界坐标系的坐标，\(\mathbf{d}\)为直线方向，是世界坐标系下的一个单位向量（笛卡尔坐标系），\(t\)是一个实数，表示从\(\mathbf{o}\)点沿视线到\(\mathbf{r}(t)\)点的距离。

3.2.2 连续

  体渲染：视线上\(\mathbf{r}\)所有的点投射到图像上形成像素颜色\(C\)的过程：

\[C(\mathbf{r}) = \int_{t_{n}}^{t_{f}} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) dt, \text{where } T(t) = \exp \left( -\int_{t_{n}}^{t} \sigma(\mathbf{r}(s)) ds \right)\]

其中，\(\mathbf{r}(t)\)为三维空间中的一个点，\(\mathbf{d}\)为视线方向，三维场景的近端和远端边界分别为\(t_{n}\)以及\(t_{f}\)；\(\mathbf{c}(\mathbf{r}(t), \mathbf{d})\)为三维点\(\mathbf{r}(t)\)从\(\mathbf{d}\)这个方向看到的颜色值；\(\sigma(\mathbf{r}(t))\)为体密度函数，反应了\(\mathbf{r}(t)\)位置的物理材质吸收光线的能力；\(T(t)\)是射线上从\(t_{n}\)到\(t\)的累积透射率。

3.2.3 离散

  将\(t_{n}\)到\(t_{f}\)拆分为\(N\)个均匀分布区间，从每个区间中随机均匀抽取一个样本\(t_i\)：

\[t_i \sim \mathcal{U} \left[t_n + \frac{i-1}{N}(t_f - t_n), t_n + \frac{i}{N}(t_f - t_n)\right] \qquad i \text{从1到} N\]

体渲染过程为

\[\hat{C}(\mathbf{r}) = \sum_{i=1}^N T_i\left(1 - \exp (-\sigma_i \delta_i)\right) \mathbf{c}_i \quad \text {where } T_i=\exp \left(-\sum_{j=1}^{i-1} \sigma_j \delta_j \right)\]

3.3 NN与位置编码

3.3.1 神经网络

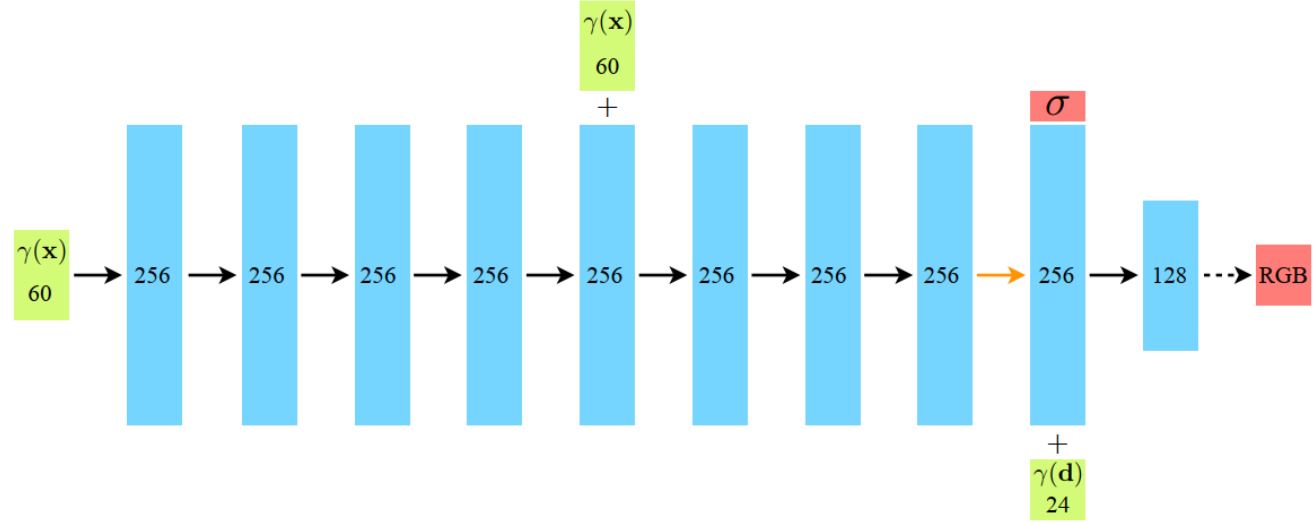
• 用途：记录辐射场信息
• 输入：坐标位置\(\mathbf{x}\)的位置编码以及视角向量\(\mathbf{d}\)的位置编码
• 输出：在坐标位置\(\mathbf{x}\)的体密度\(\sigma\)以及视线\(\mathbf{d}\)方向观察时\(\mathbf{x}\)处的的RGB值\(C\)

问题1：为什么需要视角向量？

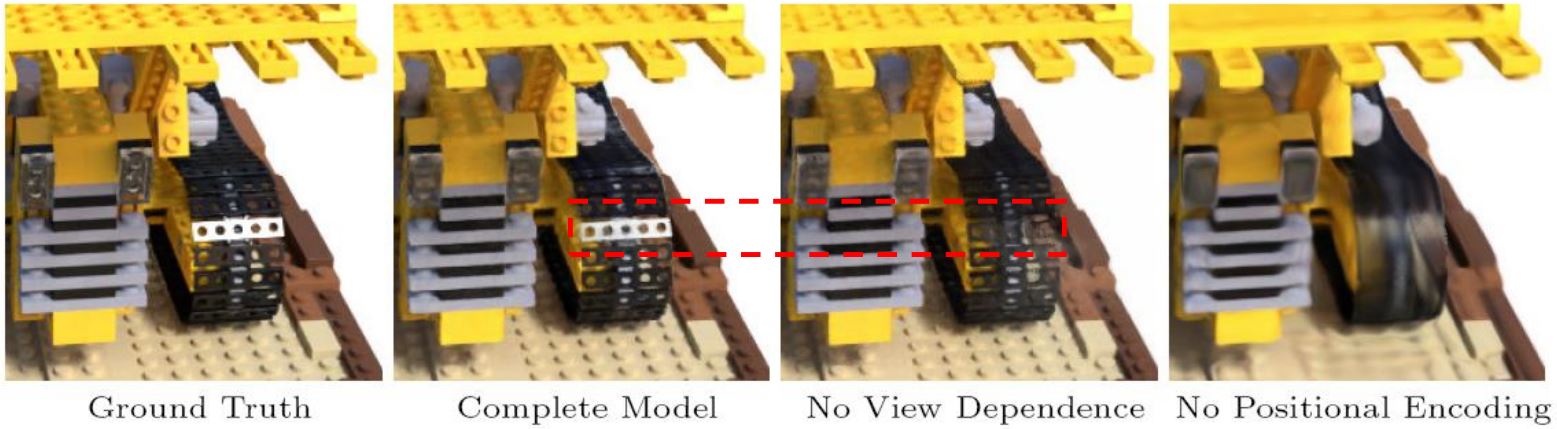
如果不考虑颜色和视角的关系，会丢失镜面反射的信息！

问题1：为什么需要位置编码？

没有位置编码的情况下，高频几何和纹理细节丢失了！

3.3.2 位置编码

  NeRF中的位置编码：

\[\gamma(p) = \big( \sin (2^0 \pi p), \cos (2^0 \pi p), \cdots, \sin (2^{L-1} \pi p), \cos (2^{L-1} \pi p) \big)\]

\(\gamma(\cdot)\)独立应用于待编码向量的各个维度，对于位置向量\(\mathbf{x}\)编码时\(L\)取10，对于视角向量\(\mathbf{d}\)编码时\(L\)取4。 经过位置编码，\(\mathbf{x}\)的编码\(\gamma(\mathbf{x})\)维度为60，\(\mathbf{d}\)的编码\(\gamma(\mathbf{d})\)维度为24。

3.4 损失函数与训练策略

• 难点：每条射线需要在近点与远点之间采样大量的点进行评估，导致计算量大
• 先验：射线上大部分区域都是空的，或者是被遮挡，对最终的颜色没有贡献。
• 策略：采用了一种"coarse to fine" 的层级采样策略，同时优化coarse网络和fine网络。

3.4.1 网络训练

  策略：采用了一种"coarse to fine" 的层级采样策略，同时优化coarse网络和fine网络。

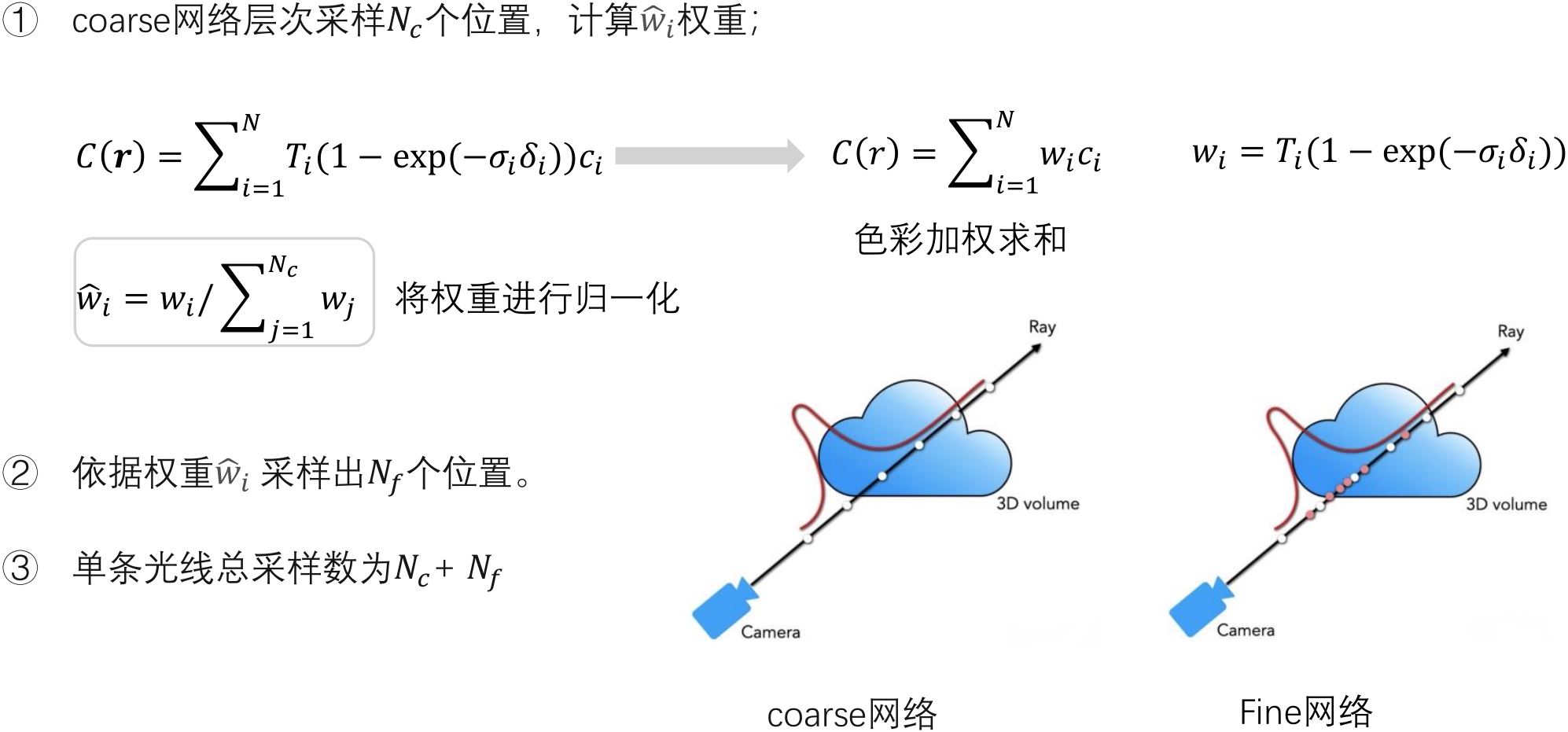
3.4..2 损失函数

  损失函数：实际颜色\(C(\mathbf{r})\)与渲染结果\(\hat{C}_c(\mathbf{r})\)的平方误差（同时优化coarse和fine两个网络）

\[\mathcal{L} = \sum_{\mathbf{r} \in \mathcal{R}} \left[ \left\| \hat{C}_c(\mathbf{r}) - C(\mathbf{r}) \right\|_2^2 + \left\| \hat{C}_f(\mathbf{r}) - C(\mathbf{r}) \right\|_2^2 \right]\]

其中，\(\mathbf{r}\)表示一条采样光线，\(\mathcal{R}\)表示所有采样光线。