Mip-NeRF

4.1 混叠与抗混叠

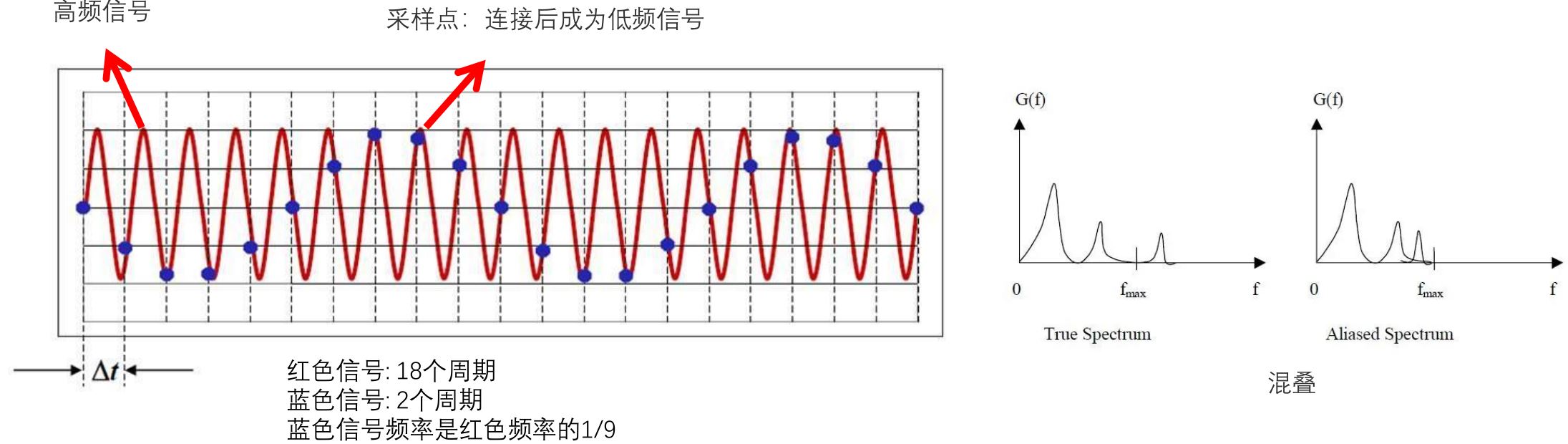
4.1.1 采样与混叠

奈奎斯特准则: 假设信号的最大频率为\(B\)，信号的采样频率为\(f_s\)，则奈奎斯特率（Nyquist rate）为\(2B\)，奈奎斯特准则是\(f_s \gt 2B\)时原始信号采样后不会丢失信息。混叠：当采样频率设置不合理时，即采样频率\(f_s\)低于2倍的信号频率（\(f_s \lt 2B\)），会导致原本的高频信号被采样成低频信号。这种频谱的重叠导致的失真称为混叠，也就是高频信号被混叠成了低频信号。

4.1.2 抗混叠

增加采样频率：提高采样频率可以使信号频率𝐵不会超过采样频率\(f_s\)的一半，从而避免混叠的发生。
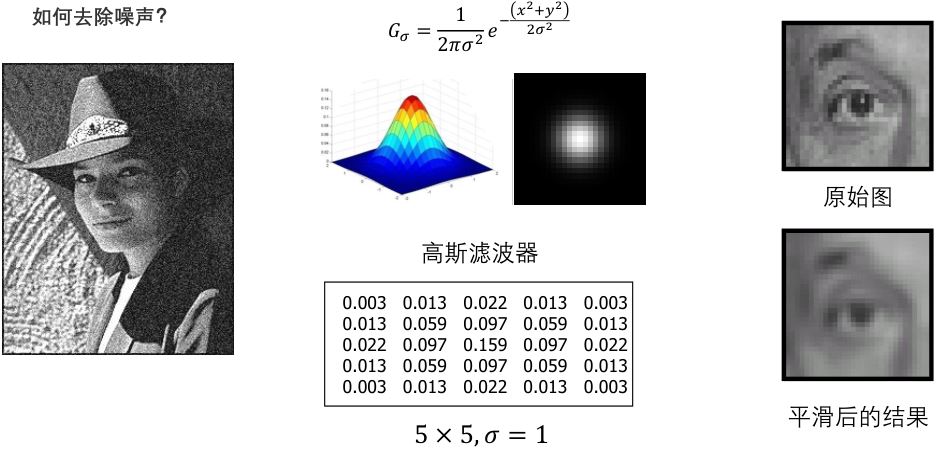
使用低通滤波器：将信号通过低通滤波器，可以去除信号中高于采样频率一半的频率分量，从而避免混叠。

抗混叠——低通滤波器
现象：出现摩尔纹
原因：采样频率过低
解决方案：采样之前，使用低通滤波器去除高于采样频率一半的频率分量。

4.2 NeRF的混叠问题

现象：原始NeRF的模型，在摄像机往远离物体方向移动时，渲染结果存在混叠。
原因：采样频率过低。
解决方案：超采样？低通滤波器？（MipMap方案）

补充

为什么增加多分辨率样本无法解决混叠问题？
当摄像机往远离物体方向移动时，同一个像素要包含更大区域的内容，但在同一条光路上神经网络只能输出一个值。

4.3 Mip-NeRF思想

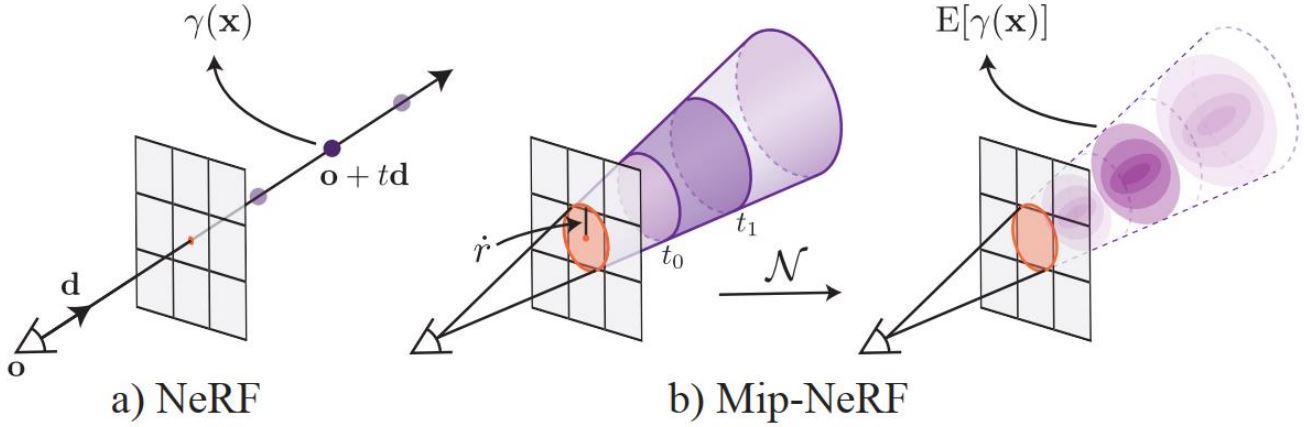
使用圆锥体取代光线，NeRF一条射线对应Mip-NeRF一个圆锥体，NeRF一个采样点对应Mip-NeRF一个圆锥截台

4.3.1 圆锥台近似计算

圆锥台采样：若\(\mathbf{x}\)位于由相机位置\(\mathbf{o}\)、视线方向\(\mathbf{d}\)、圆台半径\(\dot{r}\)、以及圆台深度区间\([t_0, t_1]\)定义的圆台中，定义\(F(\mathbf{x}, \cdot) = 1\)，

\[F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1) = 1 \left\{ \left( t_0 \lt \frac{\mathbf{d}^T (\mathbf{x}-\mathbf{o})}{\|\mathbf{d}\|_2^2} \lt t_1 \right) \wedge \left( \frac{\mathbf{d}^T(\mathbf{x}-\mathbf{o})}{\|\mathbf{d}\|_2\|\mathbf{x}-\mathbf{o}\|_2} \lt \frac{1}{\sqrt{1+(\dot{r} /\|\mathbf{d}\|_2)^2}} \right) \right\}\]

圆锥台位置编码的期望可以定义为

\[\gamma^* \left(\mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1\right) = \frac{\int \gamma(\mathbf{x}) F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1) d x} {\int F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1) d x}\]