Q-Learning
3.1 Introduction of Q-Learning
3.1.1 Critic
- 一个critic不能直接决定动作
- 给定一个actor \(\pi\),它会评价这个actor的好坏
- State value function \(V^{\pi}(s)\): 根据actor \(\pi\),在状态\(s\)时采取动作\(a\)后累计奖励的期望值
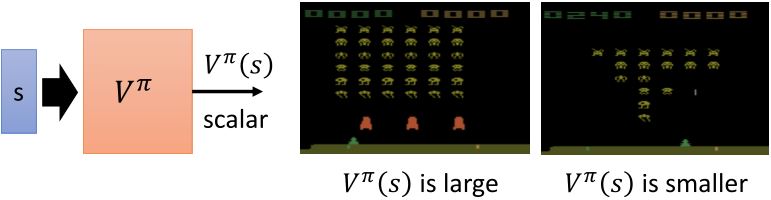
Critic的输出值取决于actor的好坏。
How to estimate ?
1. Monte-Carlo based approach
Critic观察\(\pi\)如何玩游戏。看到某个状态后,一直到episode结束所累计的奖励。
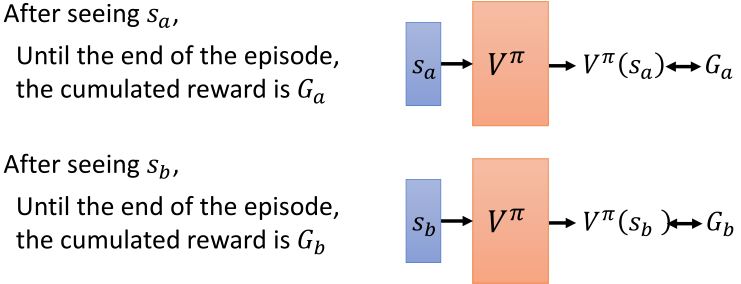
2. Temporal-difference approach
有的时候episode时间太长,把所有的学习都推迟到结束的时候太慢了。
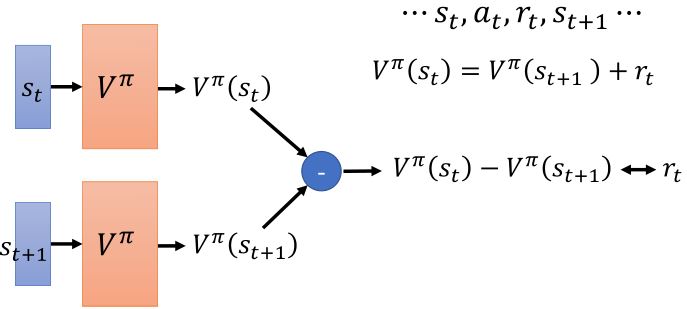
MC v.s. TD
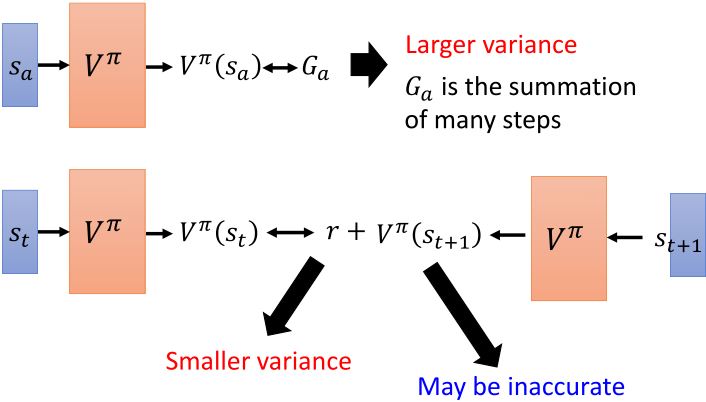
Another critic
- State-action value function \(Q^{\pi}(s,a)\): 根据actor \(\pi\),访问了状态\(s\)后累计奖励的期望值
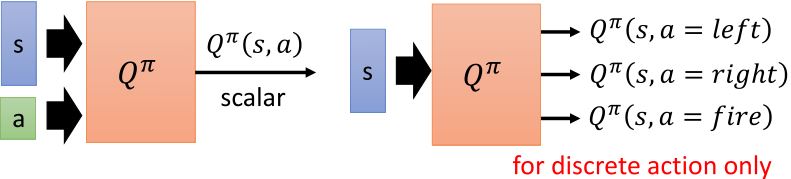
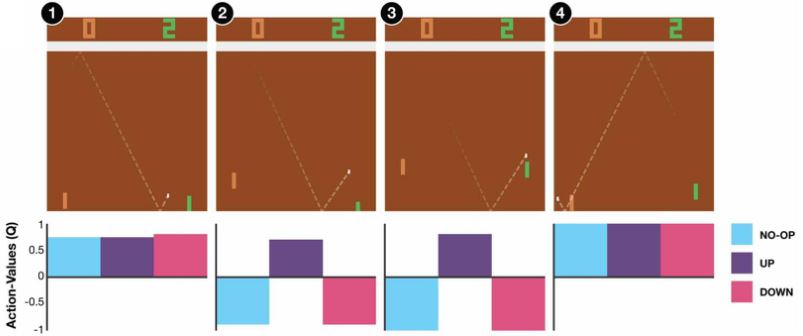
3.1.2 Q-Learning
Another way to use critic.
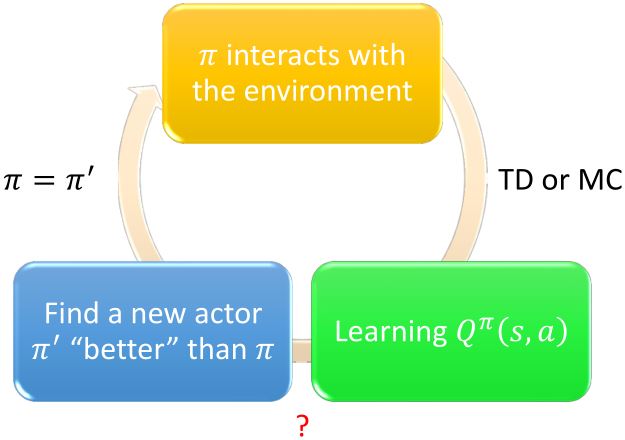
给定\(Q^{\pi}(s,a)\),找到一个新的比\(\pi\)"更好"的actor \(\pi'\)
- "更好":对于所有的状态\(s\),\(V^{\pi'}(s) \ge V^{\pi}(s)\)
\(\pi'\)没有其它参数,它由\(Q\)决定。
对连续动作\(a\)不适用
为什么\(\pi'(s) = \text{arg}\max_a Q^{\pi}(s,a)\)一定有\(V^{\pi'}(s) \ge V^{\pi}(s)\)?
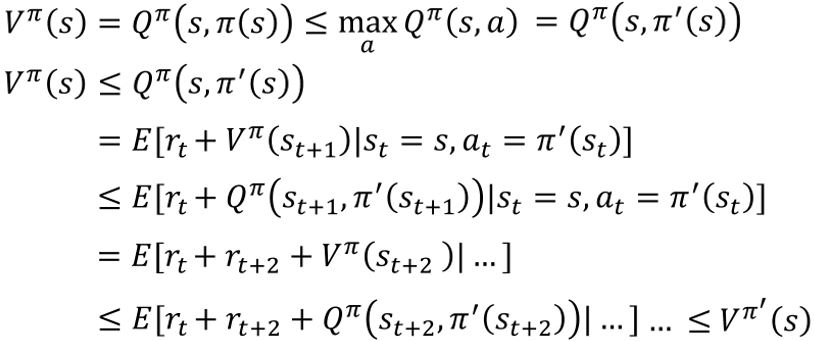
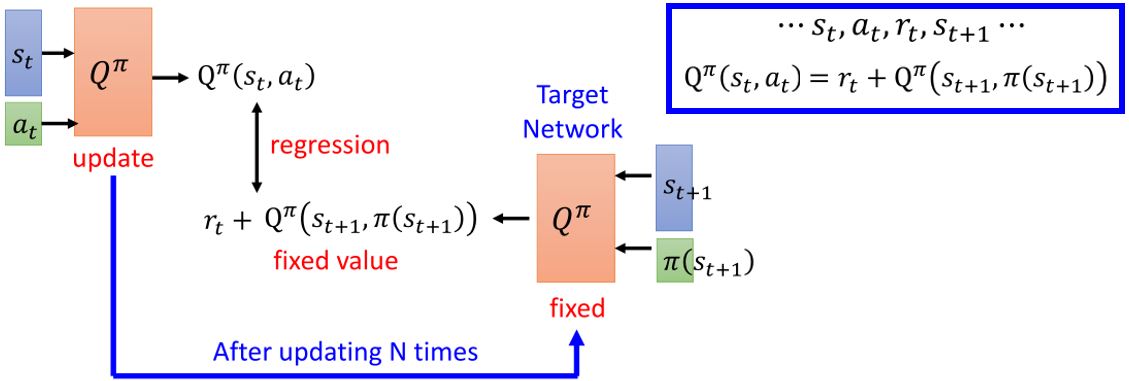
3.1.3 Target network
在实际训练中,更新目标如果不断变动会造成更新困难,所以需要用一个固定网络作为目标网络。实际操作过程中,一般会更新\(N\)次后更新一次目标网络。
3.1.4 Exploration

3.1.5 Replay buffer
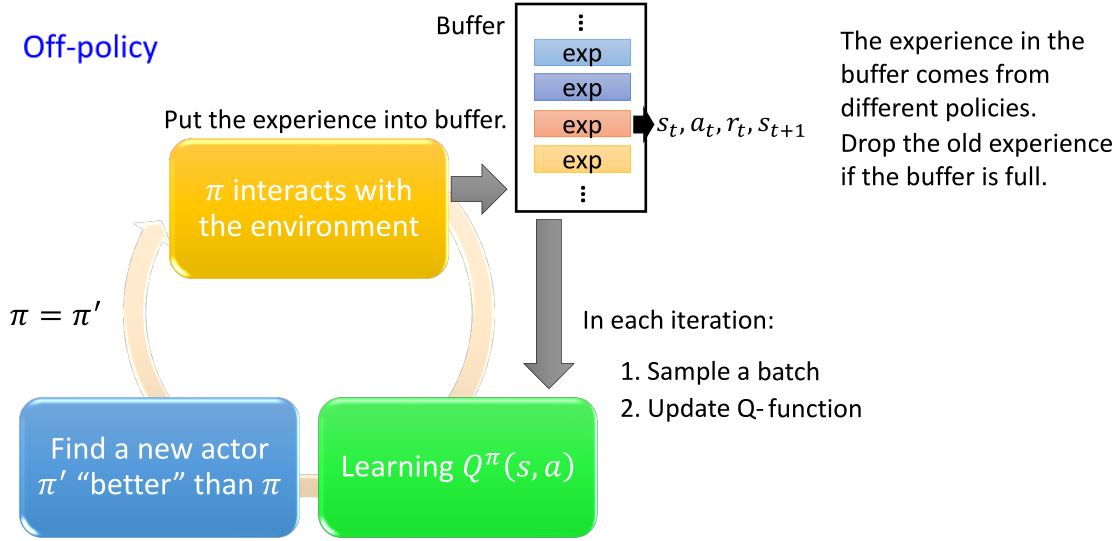
- 缩短和环境互动所花费的时间
- 使收集到的经验更加多样化
3.1.6 Typical Q-learning algorithm

3.2 Tips of Q-Learning
3.2.1 Double DQN
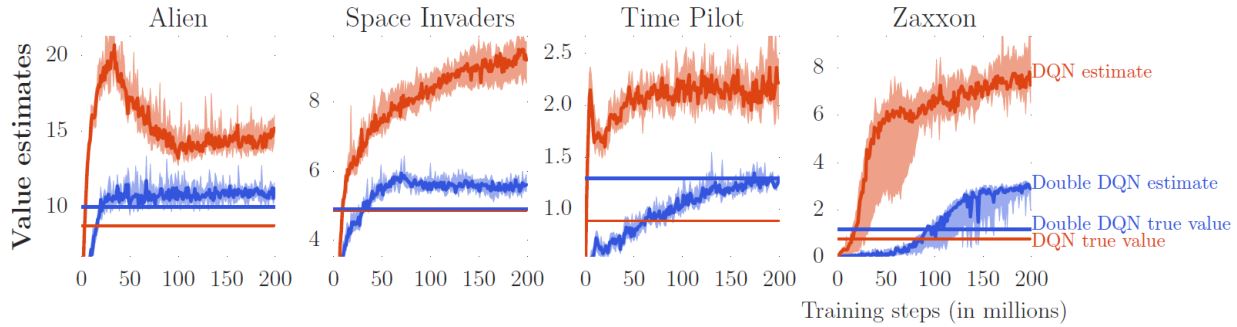

如果\(Q\)高估了\(a\),那么\(a\)会被选中,\(Q'\)会给出它的正确的值。
如果\(Q'\)高估了某个动作,那个动作是不会被\(Q\)选中的。
Hado V . Hasselt, "Double Q-learning", NIPS 2010.
Hado van Hasselt, Arthur Guez, David Silver, "Deep Reinforcement Learning with Double Q-learning", AAAI 2016.
3.2.2 Dueling DQN
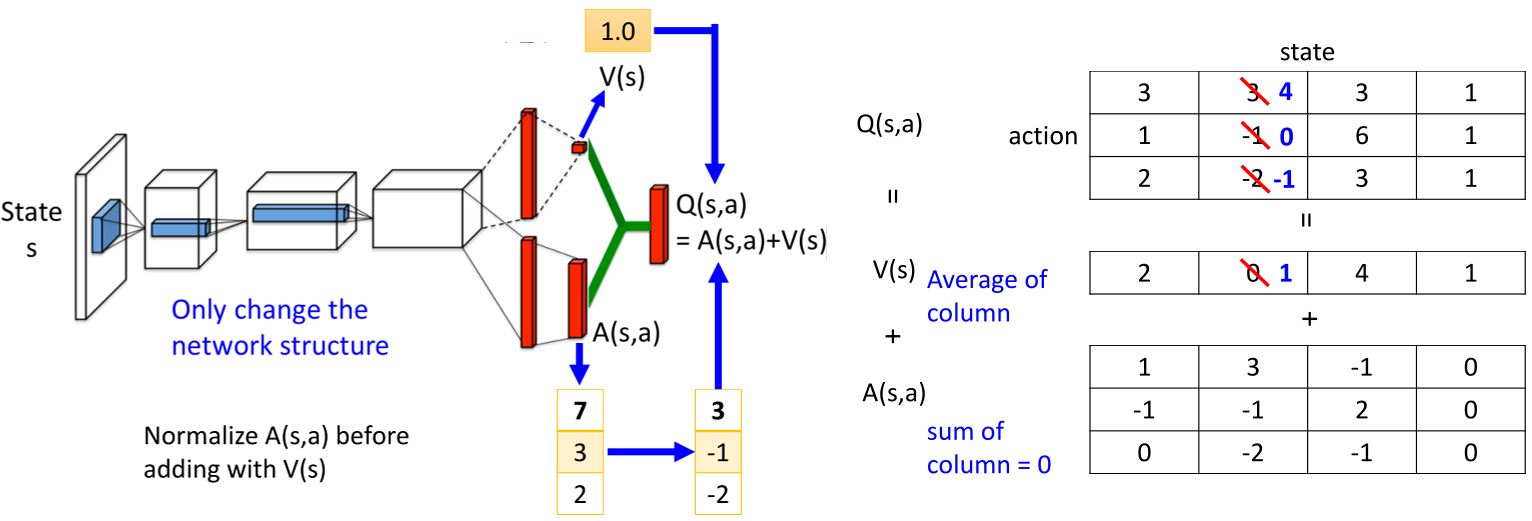
Ziyu Wang, Tom Schaul, Matteo Hessel, Hado van Hasselt, Marc Lanctot, Nando de Freitas, "Dueling Network Architectures for Deep Reinforcement Learning", arXiv preprint, 2015.
3.2.3 Prioritized replay
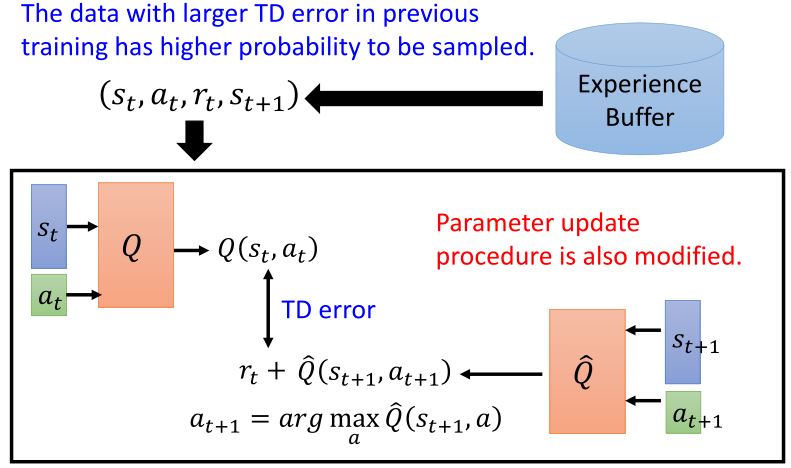
3.2.4 Multi-step
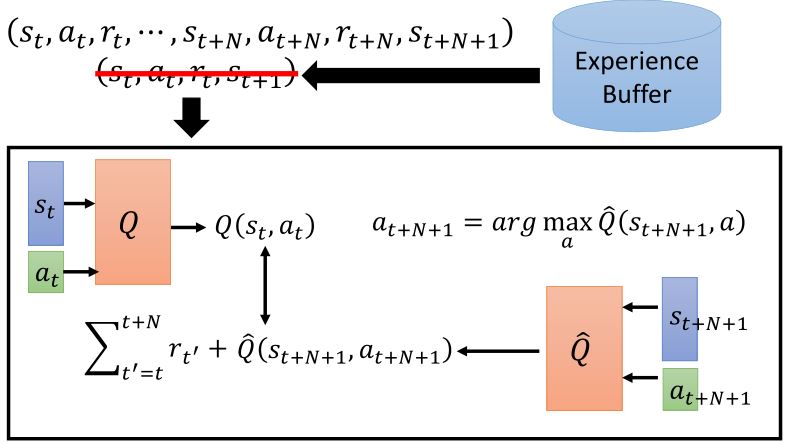
3.2.5 Noisy net


3.2.6 Distributional Q-function
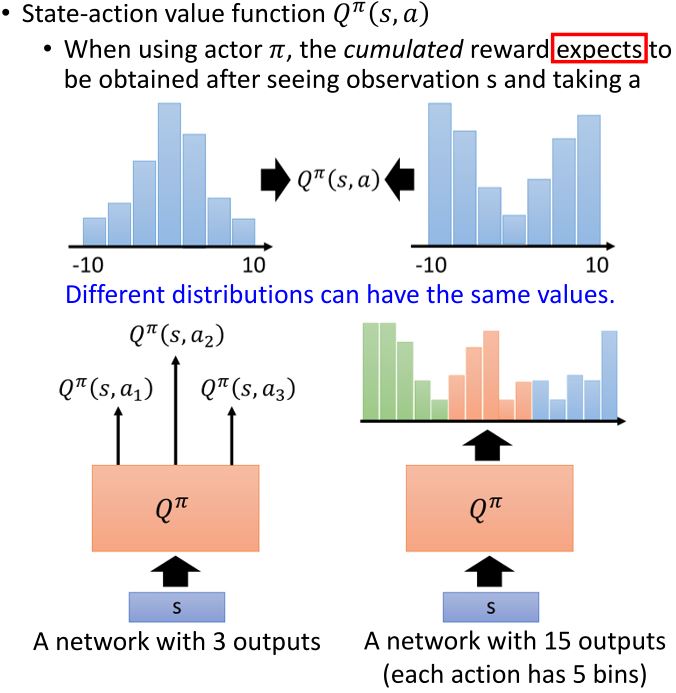
3.2.7 Rainbow
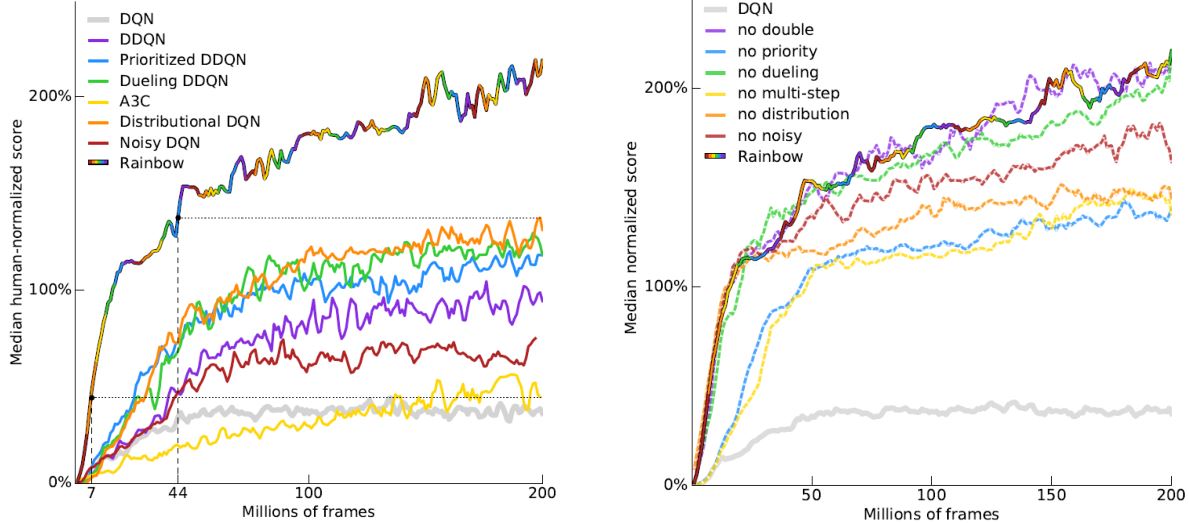
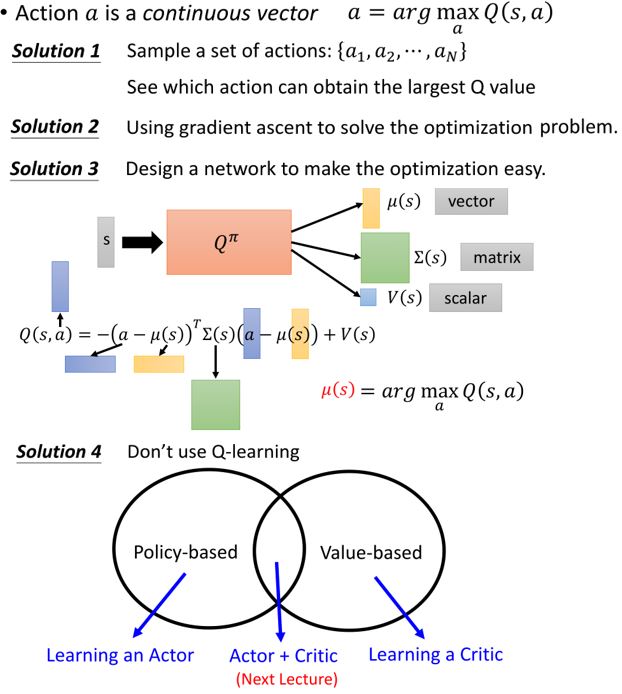
3.3 Q-Learning for Continuous Actions