Computational Complexity
计算复杂度的目标:
给出量化问题困难程度的方法;
比较两个不同问题的相对难度;
严格定义高效算法的含义;
声明一个问题的一个算法比另一个"更好"。
这部分内容只是对计算复杂度进行简单介绍,因为计算复杂度的内容很多,有专门的课程。
4.1 Computational complexity
建立问题分类的计算复杂度理论所需要的要素如下: 理论适用的问题类别\(\mathcal{C}\);
(非空)子集\(\mathcal{C}_{\mathcal{E}} \subseteq \mathcal{C}\)的"简单"问题;
(非空)子集\(\mathcal{C}_{\mathcal{H}} \subseteq \mathcal{C}\)的"困难"问题;
两组问题之间的关系 \(\triangleleft\) "不比…难"。
我们的目标只是围绕这个机制给出一些定义:
\(Q \in \mathcal{C}_{\mathcal{E}}, P \triangleleft Q \Rightarrow P \in \mathcal{C}_{\mathcal{E}}\);
\(P \in \mathcal{C}_{\mathcal{H}}, P \triangleleft Q \Rightarrow Q \in \mathcal{C}_{\mathcal{H}}\)。
4.2 Decision problem, Classes NP & P
这个理论只能应用于决策问题,有"是-否"答案的问题。
优化:\(\max \{ \mathbf{c^T x} \mid \mathbf{x} \in S \}\)
决策:\(\exists \mathbf{x} \in S\)使得\(\mathbf{c^T x} \ge k\)?
例:装箱问题(Bin Packing Problem, BPP):给定很多物品的集合\(\mathcal{S}\),每个物品有不同的尺寸,集装箱的尺寸是常数\(C\)。
优化:确定可以划分\(\mathcal{S}\)的最小子集数量,使每个子集中物品的总大小不超过\(C\)
决策:对于给定常数\(K\)决定\(\mathcal{S}\)是否可以被分成\(K\)个子集,使得每个子集中物品的总大小不超过\(C\)
所有的决策问题都可以转化成决策问题求解。
把优化转化成决策:假设你知道\(I \le z^* \le u\),其中\(I, z^*, u \in \mathbb{Z}\)。如何通过解一系列决策问题来解决这个优化问题呢?
两分法搜索:
1. if \((u - I \lt = 1), z^* = I\); exit();
2. \(k = (I + u) / 2\); if (dec(\(k\)) == false), \(I = k\); else \(u = k\); goto 1;
最多需要\(\color{green}{\log_2(u - I)}\)次调用dec(\(k\))。
4.2.1 Measuring the difficulty
我们对一个问题的复杂度感兴趣,而不是一个实例。一个问题(或模型)是由无限个实例组成的家族,其目标函数和约束有特定的结构。
可能的度量方法:
根据经验:无法实际保证任何关于给定实例的难度;
平均案例运行时间:难以分析,并且依赖于指定实例的概率分布;
最差案例运行时间:复杂性理论是基于最坏情况的方法。
4.2.2 Running time of an algorithm
算法的耗时与输入的规模有关。时间复杂度函数作为问题大小的函数,指定算法解决任何问题实例所需的最大时间量。
如何衡量问题的规模呢?
— 在合理的编码方案中表示问题所必需的信息量的长度。
— 对于一个问题实例\(X\),输入的长度\(L(X)\)为实例的"标准"表示的二进制表示的长度。
整数\(2^n \leq x \lt 2^{n+1}\)可以表示成一个向量\((v_0, v_1, \ldots, v_n)\),其中
\[x = \sum_{i=0}^n v_i 2^i, v_i \in \{0, 1\}\]注意,\(n \le \log_2 x \lt n+1\)。所以,需要对数数量的比特数来表示\(x \in \mathbb{Z}\),即\(\log_2 x + 1\)。
例:TSP问题,有\(n\)个城市,对饮成本\(c_{ij} \in \mathbb{Z}\),求\(\max_{i,j} c_{ij} = \theta\),需要\(L(X) = \log(n) + n^2 \log(\theta)\)比特来表示一个实例。
例:背包问题,\(n, a_j, c_j, b\),其中\(a_j, c_j, b\)为有理数,\(a_j \le b\),那么\(L(X) = \log(n) + (2n + 2) \log(b) + 2n \log(\theta)\),其中\(\theta = \max c_j\)。
如何度量计算时间?
— 希望这个度量与特定电脑无关;
— 计算基本运算的数量;
— 假设每个基本操作都在单位时间内完成。(只要数字的规模不增长得太快,这是合理的。)
给定一个问题\(P\)、能解决\(P\)的算法\(A\)以及问题\(P\)的一个实例\(X\):
\(L(X) =\)实例(以合理的编码方式)的长度;
\(g_A(X) =\)用算法\(A\)解决实例\(X\)需要的基本计算的量;
\(f_A(I) = \sup\{ g_A(X) \vert L(X) = I \}\)为算法\(A\)的运行时间。
\(f_A(I)\)即为\(O(g(I))\),如果存在\(c \gt 0\),使得\(f_A(I) \le c g(I)\)。考虑了函数在\(k \rightarrow \infty\)时的渐近行为。
-
算法\(A\)被称为多项式时间算法,如果\(f_A(I) = O(I^p)\)对某个固定的\(p\)。
\(A\)是强多项式时间的,如果\(f_A(I)\)的边界由一个与数据规模(数字的大小)无关的函数决定。
\(A\)是弱多项式时间的,如果\(f_A(I)\)是多项式的但不是强多项式的。\(O(I^p)\)中的\(I\)包含了与\(\log \theta\)有关的项,其中\(\theta\)是给定实例中最大的数。 -
算法\(A\)被称为指数时间算法,如果\(f_A(I) \neq O(I^p)\),对于任意的\(p\),i.e. 存在\(c_1, c_2 \gt 0, d_1, d_2 \gt 1\)和正整数\(k\)使得\(c_1 d_1^I \le f_A(I) \le c_2 d_2^I, \forall I \ge I^{\prime}\)。
-
算法\(A\)被称为伪多项式时间算法,如果\(A\)是以一元形式编码的数据长度为多项式的算法。一元的意思是我们使用一个符号的字母表。(如十进制,而非二进制)实际上,这表明\(A\)与参数和实例数据\(\theta\)的大小有多项式关系,而不是\(\log \theta\)。
例:整数背包问题,存在一个\(O(Nb)\)的算法可以解这个问题,其中,\(N\)是物品的数量,\(b\)是背包的大小。这不少一个多项式时间算法。如果\(b\)由关于\(n\)的多项式函数决定的话,那么这个算法是多项式时间的。
令\(\theta\)为给定实例中的最大数字。输入数据的长度为\(I = O(\log(\theta))\)。如果算法需要\(\theta\)步,那么这是一个指数时间算法!因为\(f_A(I) \ge O(\theta) = O(2^I)\)。
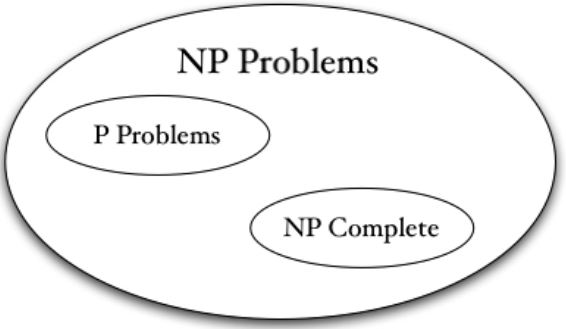
4.2.3 Classes NP & P
The class NP
- 问题类型NP \(\neq\) "Non-polynomial"
- NP = 在非确定性图灵机上可以在多项式时间内解决的一类决策问题。
- NP \(\approx\) 一类决策问题,这类问题具有对于每一个答案是"yes"的实例,都有一个简短的(多项式)证明的性质。(即证明答案是"yes"很容易)
我们只能研究很快就能验证答案是否正确的问题,而验证一个问题简单与解决这个问题是否简单无关。
- 如果一个优化问题对应的决策问题是NP的,那么这个优化问题可以通过多项式时间次数回答决策问题得到解决。
- P是NP问题中可以在多项式时间内被解决的那类。
例:对于一个0-1背包问题实例\(X\)。
决策问题:存在\(x \in S = \{ x \in \{0, 1\}^n \mid a^T x \le b \}\)使得\(c^T x \ge k\)吗?
输入的长度:\(L(X) = \log(n) + 2n \log(\theta) + \log b + \log k\)。
对于一个实例,如果它的答案是"yes",那么它满足:
(a) 读一个解\(x \in \{0, 1\}^n\);
(b) 检查\(a^T x \le b\)和\(c^T x \ge k\)。
(a)和(b)都可以在\(L\)的多项式时间内完成。
问:整数背包问题呢?
— 整数背包问题也是有多项式时间的算法的。
P问题:
-
具有非负权重的最短路径问题:\(O(m^2)\)。这个问题中计算的次数与边权重的大小无源,所以是强多项式时间的。
-
解方程组\(Ax = b\)。
(a) 通过高斯消元法即可找到解\(x = A^{-1}b\),\(n\)次pivots且每次pivot需要\(O(n^2)\)次计算。所以总计算量为\(O(n^3)\)。
(b) 出现的数的大小受限于\((A, b)\)的任意子矩阵的最大行列式。由于\(\det(A)\)包含\(n! \lt n^n\)项,所以这个最大的数由\((n \theta)^n\)决定,其中\(\theta\)是\((A, b)\)中最大的。这表明这个表达式的规模受限于一个与\(n\)和\(\log \theta\)相关的多项式函数:\(\log((n \theta)^n) = n \log(\theta)\)。
(c) 与输入的规模成多项式关系。 -
指派问题:\(O(n^4)\)。
-
线性规划:\(\min \{ c^T x \mid Ax = b, x \ge 0 \}\)。
算法:George Dantzig在1947年提出了单纯形法。但是,单纯形法有表现很差的反例,所以很长时间内人们都是不知道线性规划是否有多项式算法的。直到1979年,Leonid Khachiyan提出了椭球法,该方法在最坏的情况下也是多项式时间的,但是该方法一般来说表现都比单纯形法差,难以实现。到了1984年,N. Karmarkar提出了内点法并用程序实现了内点法(其复杂度为\(O(n^4 L)\))。1990s后有了路径跟随法。
Open problem in LP:LP存在强多项式算法吗?
The class co-NP
这类问题的补问题是NP的。
co-NP \(\approx\) 一类决策问题,这类决策问题具有对于每个有"no"回答的实例,都有简短的证明的特性。
4.3 Polynomial Reduction & The Class NPC
如果问题\(P, Q \in\) NP,并且如果\(P\)的一个实例可以在多项式时间内被转化成\(Q\)的一个实例,那么\(P\)是polynomially reducible到\(Q\)。我们可以写成\(P \triangleleft Q\)。
现在,我们想问一个问题:NP问题中最难的是什么?
如果\(P \in\) NPC (NP-complete),那么\(Q \in\) NP \(\Rightarrow Q \triangleleft P\)。
如果\(P \in\) NP且我们可以在多项式时间内将任意其它问题\(Q \in\) NP转化成\(P\),那么在这个意义上\(P\)就是NP中最难的问题。
如果一个优化问题对应的决策问题是NPC的,那么这个优化问题是NP-hard问题。
Stephen A. Cook于1970年证明了Satisfiability problem是NPC的。满足性问题是第一个已知的NPC问题!Stephen A. Cook于1982年获得了图灵奖。
满足性问题:给定\(N = \{ 1, \ldots, n \}\)和\(2m\)个子集\(\{C_i\}_{i=1}^m\)和\(\{D_i\}_{i=1}^m\)。是否存在\(x \in \{0,1\}^n\)使得\(\sum_{j \in C_i} x_j + \sum_{j \in D_i}(1- x_j) \ge 1\)?
4.4 P vs NP Problem
\(Q \in\) P, \(P \triangleleft Q \Rightarrow P \in\) P.
\(P \in\) NPC, \(P \triangleleft Q \Rightarrow Q \in\) NPC.
P vs NP Problem – Clay Mathematics Institute

