Policy Optimization Ⅰ

5.1 Policy-based RL

确定性策略是直接从价值函数用贪心策略\(a_t = \text{arg} \max_a Q(a, s_t)\)得到的。与之相反，可以使用将策略函数参数化表示为\(\color{green}{\pi_{\theta} (a \vert s)}\)，其中\(\color{green}{\theta}\)是可学习的策略参数，输出是动作集上的概率。对于策略优化，只需要知道策略中的动作，然后直接优化策略。

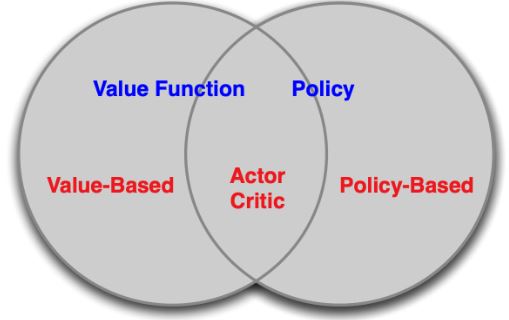
Value-based RL vs. Policy-based RL:

value-based RL：学习价值函数基于价值函数的隐性策略
policy-based RL：没有价值函数直接学习策略
actor-critic：学习策略函数和价值函数

基于策略的强化学习优势：

更好的收敛性：能保证收敛到某个局部最优（最差的情况）或全局最优（最好的情况）
策略梯度对于高维动作空间更高效
策略梯度可以学习随机策略，而价值函数不可以

劣势：

一般都会收敛到局部最优
评估策略的方差很大

两种策略：

确定性：给定一个状态，策略会返回一个确定的动作来采取。
随机性：给定一个状态，策略会返回动作的概率分布（e.g. 40%的概率向左转，60%的概率向右转）或连续动作的某个高斯分布。

例：石头剪刀布
该游戏有两个玩家，什么样的策略是最好的呢？如果策略是固定的，那么很容易被打败。所以，均匀随机策略是最优的（Nash均衡）。

例：aliased gridworld

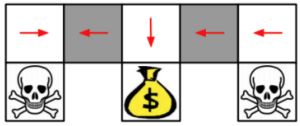
在这个游戏中，agent无法分辨这两个灰色的格子。考虑以下特性（对于所有的上下左右），\(\psi (s, a) = [1(\text{上面是墙}, a = \text{向右移}), 1(\text{下面是墙}, a = \text{向左移}), \ldots]\)。
如果是基于价值的RL，价值函数近似为\(Q_{\theta} (s, a) = f(\psi(s, a), \theta)\)
如果是基于策略的RL，策略函数近似为\(\phi_{\theta} (s, a) = g(\psi(s, a), \theta)\)

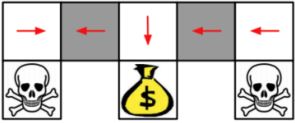
基于价值的RL会学到一个确定策略，e.g. 贪心。因为无法区分两个灰色格子，所以得到的最优确定性策略要么就是都往左（如图所示），要么就是都往右。不管是哪个，都有50%的概率会卡住。

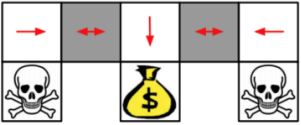
基于策略的RL会学到一个随机策略。一个最优的随机性策略会在遇到这两个灰色格子的状态下，随机选择向左或向右，以一半一半的概率。这样对于任何一个起始点，agent都很有可能在几步之内到达目标状态。

5.1.1 Objective of optimizing policy

目标：给定义一个关于参数\(\theta\)的策略近似器\(\pi_{\theta}(s,a)\)，找到最好的\(\theta\)

问：如何衡量策略\(\pi_{\theta}\)的质量？

在episodic环境中，可以用第一个值

\[J_{1}(\theta) = V^{\pi_{\theta}}\left(s_{1}\right) = \mathbb{E}_{\pi_{\theta}}\left[v_{1}\right]\]

在连续环境中，可以用平均价值

\[J_{a v V}(\theta) = \sum_{s} d^{\pi_{\theta}}(s) V^{\pi_{\theta}}(s)\]

或每个时间步长的平均奖励

\[J_{a v R}(\theta) = \sum_{s} d^{\pi_{\theta}}(s) \sum_{a} \pi_{\theta}(s, a) R(s, a)\]

其中，\(d^{\pi_{\theta}}\)是\(\pi_{\theta}\)下Markov链的静态分布。

策略的价值的定义：

\[\color{green}{\begin{aligned} J(\theta) &= \mathbb{E}_{\tau \sim \pi_{\theta}}\left[\sum_{t} R\left(s_{t}^{\tau}, a_{t}^{\tau}\right)\right] \\ & \approx \frac{1}{m} \sum_{m} \sum_{t} R\left(s_{t}^{m}, a_{t}^{m}\right) \end{aligned}}\]

这和先前在基于价值的强化学习中定义的价值函数是一样的。

这里\(\tau\)是按策略函数\(\pi_{\theta}\)采样的轨迹
这里先忽略折扣因子

基于策略的强化学习的目标：

\[\color{green}{ \theta^* = \text{arg} \max_{\theta} \mathbb{E}_{\tau \sim \pi_{\theta}} \left[\sum_{t} R\left(s_{t}^{\tau}, a_{t}^{\tau}\right)\right] }\]

5.1.2 Policy optimization

基于策略的强化学习是一个优化问题，找到能最大化\(J(\theta)\)的\(\theta\)。

如果\(J(\theta)\)是可微的，那么可以使用基于梯度的方法：1. 梯度上升 2. 共轭梯度 3. 准牛顿法

如果\(J(\theta)\)是不可微的，或者导数计算比较麻烦，那么可以使用一些无需导数的黑箱优化方法：1. 交叉熵法（CEM） 2. 爬山算法 3. 进化算法

Using derivative

函数\(J(\theta)\)为策略目标函数。目标：通过沿策略的梯度上升，找到能够使\(J(\theta)\)最大的参数\(\theta^*\)。沿梯度方向调整\(\theta\)，其中\(\alpha\)为步长。

\[\Delta \theta = \alpha \nabla_{\theta} J(\theta)\]

定义\(J(\theta)\)的梯度为\(\nabla_{\theta} J(\theta) = \left( \frac{\partial J(\theta)}{\partial \theta_1}, \frac{\partial J(\theta)}{\partial \theta_2}, \cdots, \frac{\partial J(\theta)}{\partial \theta_n}, \right)^T\)。

Using derivative-free methods

1. Cross-entropy method (CEM)

最优参数\(\theta^* = \text{arg} \max J(\theta)\)
把\(J(\theta)\)当作一个黑箱得分函数（不可微）

例：一个简单的强化学习问题的CEM例子

补充

在有些环境中，基于CEM的方法非常高效，可能比可以优化的强化学习办法效果好。

2. Approximate Gradients by Finite Difference

要评估\(\pi_{\theta}(s, a)\)的策略梯度，对于每个维度\(k \in [1, n]\)，通过在\(\theta\)的第\(k\)维附近制造一个小的扰动量\(\epsilon\)来估计目标函数的第\(k\)个偏微分。

\[\frac{\partial J(\theta)}{\partial \theta_k} \approx \frac{J(\theta + \epsilon u_k) - J(\theta)}{\epsilon}\]

其中，\(u_k\)是第\(k\)个元素为1，其余元素为0的单位向量。

尽管这个方法有噪声且效率低，但是它对任意策略都有效，即使策略是不可微的。

5.1.3 Computing the PG analytically

假设策略\(\pi_{\theta}\)在非零时是可微的，可以计算出它的梯度为\(\nabla_{\theta} \pi_{\theta} (s, a)\)。利用似然比的技巧

\[\nabla_{\theta} \pi_{\theta} (s, a) = \pi_{\theta} (s, a) \frac{\nabla_{\theta} \pi_{\theta} (s, a)}{\pi_{\theta} (s, a)} = \pi_{\theta} (s, a) \nabla_{\theta} \log \pi_{\theta} (s, a)\]

得分函数（score function）为\(\nabla_{\theta} \log \pi_{\theta} (s, a)\)。

Policy example: softmax policy

简单策略模型：用特征的线性组合\(\phi (s,a)^T \theta\)来衡量动作
动作的概率与期望权重成正比 \(\pi_{\theta} (s, a) = \frac{\exp^{\phi (s,a)^T \theta}}{\sum_{a'} \exp^{\phi (s,a')^T \theta}}\)
得分函数为\(\nabla_{\theta} \log \pi_{\theta} (s, a) = \phi (s, a) - \mathbb{E}_{\pi_{\theta}} [\phi (s, .)]\)

Policy example: Gaussian policy

在连续动作空间中，可以定义一个高斯策略

均值是状态特征的线性组合 \(\mu(s) = \phi(s)^T \theta\)
方差可以固定为\(\sigma^2\)或者是参数化的
策略是高斯分布的、连续的 \(a \sim \mathcal{N}(\mu(s), \sigma^2)\)
得分函数为\(\nabla_{\theta} \log \pi_{\theta} (s, a) = \frac{(a - \mu(s)) \phi(s)}{\sigma^2}\)

5.2 Monte-Carlo Policy Gradient

5.2.1 PG for one-step MDPs

考虑一类简单的one-step MAPs，从状态\(s \sim d(s)\)开始，在一步之后结束，奖励为\(r = R(s, a)\)。用似然比来计算策略梯度

\[J(\theta) = \mathbb{E}_{\pi_{\theta}} [r] = \sum_{s \in \mathcal{S}} d(s) \sum_{a \in \mathcal{A}} \pi_{\theta}(s, a) r\]

梯度为

\[\begin{aligned} \nabla_{\theta} J(\theta) =& \sum_{s \in \mathcal{S}} d(s) \sum_{a \in \mathcal{A}} \pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta}(s, a) r \\ =& \mathbb{E}_{\pi_{\theta}} [r \nabla_{\theta} \log \pi_{\theta}(s, a)] \end{aligned}\]

5.2.2 PG for multi-steps MDPs

从一个episode得到的状态-动作轨迹可以表示为\(\tau=\left(s_{0}, a_{0}, r_{1}, \ldots s_{T-1}, a_{T-1}, r_{T}, s_{T}\right) \sim\left(\pi_{\theta}, P\left(s_{t+1} \mid s_{t}, a_{t}\right)\right)\)，沿着轨迹\(\tau\)得到的奖励总和为\(R(\tau) = \sum_{t=0}^{T-1} R(s_t, a_t)\)。

策略目标为

\[J(\theta) = \mathbb{E}_{\pi_{\theta}}\left[\sum_{t=0}^{T-1} R\left(s_{t}, a_{t}\right)\right] = \sum_{\tau} P(\tau ; \theta) R(\tau)\]

其中\(P(\tau ; \theta)=\mu\left(s_{0}\right) \prod_{t=0}^{T-1} \pi_{\theta}\left(a_{t} \mid s_{t}\right) p\left(s_{t+1} \mid s_{t}, a_{t}\right)\)表示当执行策略\(\pi_{\theta}\)时沿轨迹\(\tau\)的概率。

我们的目标就是找到策略参数\(\theta\)

\[\theta^{*} = \underset{\theta}{\arg \max} J(\theta) = \underset{\theta}{\arg \max} \sum_{\tau} P(\tau ; \theta) R(\tau)\]

对\(\theta\)求梯度

\[\begin{aligned} \nabla_{\theta} J(\theta) &= \nabla_{\theta} \sum_{\tau} P(\tau ; \theta) R(\tau) \\ &= \sum_{\tau} \nabla_{\theta} P(\tau ; \theta) R(\tau) \\ &= \sum_{\tau} \frac{P(\tau ; \theta)}{P(\tau ; \theta)} \nabla_{\theta} P(\tau ; \theta) R(\tau) \\ &= \sum_{\tau} P(\tau ; \theta) R(\tau) \frac{\nabla_{\theta} P(\tau ; \theta)}{P(\tau ; \theta)} \\ &= \sum_{\tau} P(\tau ; \theta) R(\tau) \nabla_{\theta} \log P(\tau ; \theta) \end{aligned}\]

用在策略\(\pi_{\theta}\)下的\(m\)条采样路径的经验估计来近似

\[\nabla_{\theta} J(\theta) \approx \frac{1}{m} \sum_{i=1}^{m} R\left(\tau_{i}\right) \nabla_{\theta} \log P\left(\tau_{i} ; \theta\right)\]

将轨迹分解为状态和动作

将\(\nabla_{\theta} \log P\left(\tau_{i} ; \theta\right)\)分解

\[\begin{aligned} \nabla_{\theta} \log P(\tau ; \theta) &= \nabla_{\theta} \log \left[\mu\left(s_{0}\right) \prod_{t=0}^{T-1} \pi_{\theta}\left(a_{t} \mid s_{t}\right) p\left(s_{t+1} \mid s_{t}, a_{t}\right)\right] \\ &= \nabla_{\theta}\left[\log \mu\left(s_{0}\right)+\sum_{t=0}^{T-1} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)+\log p\left(s_{t+1} \mid s_{t}, a_{t}\right)\right] \\ &= \sum_{t=0}^{T-1} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \end{aligned}\]

补充

利用likelihood ratio trick，在求偏微分时，通过log把连乘转换成连加，并且只留下了score function的那一项。

5.2.3 Likelihood ratio PG

我们的目标就是找到策略参数\(\theta\)，

\[\theta^{*} = \underset{\theta}{\arg \max} J(\theta) = \underset{\theta}{\arg \max} \sum_{\tau} P(\tau ; \theta) R(\tau)\]

用在策略\(\pi_{\theta}\)下的\(m\)条采样路径的经验估计来近似\(\nabla_{\theta} J(\theta) \approx \frac{1}{m} \sum_{i=1}^{m} R\left(\tau_{i}\right) \nabla_{\theta} \log P\left(\tau_{i} ; \theta\right)\)。

然后我们有

\[\nabla_{\theta} \log P\left(\tau_{i} ; \theta\right)=\sum_{t=0}^{T-1} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\] \[\nabla_{\theta} J(\theta) \approx \frac{1}{m} \sum_{i=1}^{m} R\left(\tau_{i}\right) \sum_{t=0}^{T-1} \nabla_{\theta} \log \pi_{\theta}\left(a_{t}^{i} \mid s_{t}^{i}\right)\]

无需知道动态模型！！！

5.3 Reduce the Variance of PG

5.3.1 Understanding score function gradient estimator

\(\mathbb{E}_{\tau \sim \pi_{\theta}} [R(\tau)]\)的一般形式为计算函数\(f(x)\)期望的梯度，即

\[\begin{aligned} \nabla_{\theta} \mathbb{E}_{p(x;\theta)}[f(x)] &= \mathbb{E}_{p(x;\theta)} [f(x) \nabla_{\theta} \log{p(x;\theta)}] \\ &\approx \frac{1}{S} \sum_{s=1}^S f(x_s) \nabla_{\theta} \log{p(x_s;\theta)} \ , \text{where } x_s \sim p(x;\theta) \end{aligned}\]

这个梯度可以理解为：
调整参数\(\theta\)使得分布\(p\)未来的采样\(x\)在\(f(x)\)的评价中更高的得分。
按与方向\(f(x_s) \nabla_{\theta} \log{p(x_s;\theta)}\)有多好成比例地提高样本的对数似然度。

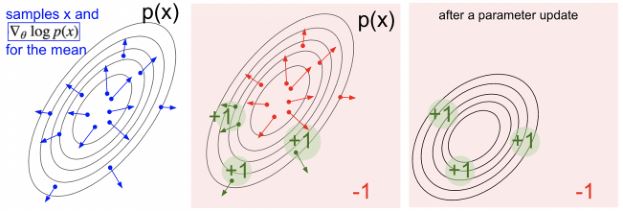
与极大似然相比：

两者的梯度
Policy gradient estimator：\(\nabla_{\theta} J(\theta) \approx \frac{1}{M} \sum_{m=1}^M \left( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta}(a_{t,m} \vert s_{t,m}) \right) \left( \sum_{t=1}^T r(a_{t,m} \vert s_{t,m}) \right)\)
Maximum likelihood estimator：\(\nabla_{\theta} J_{ML}(\theta) \approx \frac{1}{M} \sum_{m=1}^M \left( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta}(a_{t,m} \vert s_{t,m}) \right)\)

也就是说，好的动作变得更有可能，坏的动作变得更不可能。

\[\nabla_{\theta} J(\theta) \approx \frac{1}{m} \sum_{i=1}^m R(\tau_i) \nabla_{\theta} \log P(\tau_i ; \theta)\]

如果上山可以得到更多reward，那么就调整策略参数来增加轨迹向高处移动的可能性

Large Variance of Policy Gradient

我们有如下的近似更新：

\[\nabla_{\theta} J(\theta) \approx \frac{1}{m} \sum_{i=1}^m R(\tau_i) \sum_{t=0}^{T-1} \nabla_{\theta} \log \pi_{\theta}(a_t^i \vert s_t^i)\]

这个估计是无偏的但是非常noisy（因为对策略梯度的求解是通过MC方法采样来近似的）。两种解决方案：

Use temporal causality
Include a baseline

5.3.2 Using causality

之前的策略梯度为\(\nabla_{\theta} \mathbb{E}_{\tau}[R] = \mathbb{E}_{\tau} \left[ \left( \sum_{t=0}^{T-1} r_t \right) \left( \sum_{t=0}^{T-1} \nabla_{\theta} \log \pi_{\theta}(a_t \vert s_t) \right) \right]\)，可以理解为根据\(r_t\)对log likelihood做加权，然而前面的log likelihood并不会对后面的reward造成影响，因为实际上\(t=t'\)时刻的reward只受到在\(t=0\)到\(t=t'\)之间的likelihood的影响。

我们可以推导出单个奖励项的梯度估计为

\[\nabla_{\theta} \mathbb{E}_{\tau} [r_t'] = \mathbb{E}_{\tau} [r_t' \sum_{t=0}^{t'} \nabla_{\theta} \log \pi_{\theta}(a_{t} \mid s_{t})]\]

把这个式子按\(t\)求和，得到

\[\begin{aligned} \nabla_{\theta} J(\theta) = \nabla_{\theta} \mathbb{E}_{\tau \sim \pi_{\theta}}[R] &= \mathbb{E}_{\tau}\left[\sum_{t^{\prime}=0}^{T-1} r_{t^{\prime}} \sum_{t=0}^{t^{\prime}} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] \\ &= \mathbb{E}_{\tau}\left[\sum_{t=0}^{T-1} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \sum_{t^{\prime}=t}^{T-1} r_{t^{\prime}}\right] \\ &= \mathbb{E}_{\tau}\left[\sum_{t=0}^{T-1} G_{t} \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] \end{aligned}\] \[\nabla_{\theta} \mathbb{E}_{\tau \sim \pi_{\theta}}[R] = \mathbb{E}_{\tau}\left[\sum_{t=0}^{T-1} G_{t} \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right]\]

其中\(G_t = \sum_{t'=t}^{T-1} r_{t'}\)是轨迹在step \(t\)时的return
Causality：当\(t \le t'\)时，\(t'\)时刻的策略无法影响\(t\)时刻的reward

最终，我们有如下的估计更新

\[\color{green}{ \nabla_{\theta} \mathbb{E}[R] \approx \frac{1}{m} \sum_{i=1}^{m} \sum_{t=0}^{T-1} G_{t}^{(i)} \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t}^{i} \mid s_{t}^{i}\right) }\]

REINFORCE: A MC PG algorithm

该算法简单地按照策略\(\pi_{\theta}\)对多个轨迹进行采样，同时使用估计的梯度更新\(\theta\)。

经典论文：Williams (1992). Simple statistical gradient-following algorithms for connectionist reinforcement learning: introduces REINFORCE algorithm.

5.3.3 Using baseline

原来的更新中\(G_t = \sum_{t'=t}^{T-1} r_{t'}\)是可能方差很大的轨迹的return，所以我们可以给策略梯度减去一个baseline \(b(s)\)来抑制方差

\[\nabla_{\theta} \mathbb{E}_{\tau \sim \pi_{\theta}}[R] = \mathbb{E}_{\tau} \left[\sum_{t=0}^{T-1} \color{green}{(G_{t}-b(s_t))} \color{black}{\cdot} \nabla_{\theta} \log \pi_{\theta}(a_{t} \mid s_{t})\right]\]

也就是说：以与return \(G_t\)比expected return好多少成比例的方式增加动作\(a_t\)的logprob。

我们可以证明baseline \(b(s)\)是可以减少方差而不改变期望的，即\(\mathbb{E}_{\tau} \big[ \nabla_{\theta} \log \pi_{\theta}(a_{t} \vert s_{t}) b(s_t) \big] = 0\)，\(\mathbb{E}_{\tau} \big[\nabla_{\theta} \log \pi_{\theta}\left(a_{t} \vert s_{t}\right)\left(G_{t}-b\left(s_{t}\right)\right) \big] = \mathbb{E}_{\tau} \big[\nabla_{\theta} \log \pi_{\theta}\left(a_{t} \vert s_{t}\right) G_{t} \big]\)，\(\operatorname{Var}_{\tau} \big[\nabla_{\theta} \log \pi_{\theta}\left(a_{t} \vert s_{t}\right)\left(G_{t}-b\left(s_{t}\right)\right) \big] <\operatorname{Var}_{\tau} \big[\nabla_{\theta} \log \pi_{\theta}\left(a_{t} s_{t}\right) G_{t} \big]\)。因此，减去一个baseline在期望上是无偏的，但会减少方差。

一个好用的baseline是expected return：\(b(s_t) = \mathbb{E} [r_t + t_{t+1} + \ldots + r_{T-1}]\)。或者，我们也可以使用参数化的\(b_{\mathbf{w}}(s_t)\)

\[\nabla_{\theta} J(\theta) = \mathbb{E}_{\tau} \left[\sum_{t=0}^{T-1} \color{green}{(G_{t}-b_{\mathbf{w}}(s_t))} \color{black}{\cdot} \nabla_{\theta} \log \pi_{\theta}(a_{t} \mid s_{t})\right]\]

Baseline \(b(s)\)可以减小方差，且不会改变期望
Baseline \(b_{\mathbf{w}}(s_t)\)的参数\(\mathbf{w}\)也需要学习，所以我们有两组参数\(\mathbf{w}\)和\(\theta\)

Vanilla PG algorithm with baseline

经典论文：Sutton, McAllester, Singh, Mansour (1999). Policy gradient methods for reinforcement learning with function approximation.

5.4 Actor-Critic

5.4.1 Using a Critic

更新为\(\nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}}\left[\sum_{t=0}^{T-1} G_{t} \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right]\)。在实际用的时候，\(G_t\)是MC策略梯度的一个采样，它是对\(Q^{\pi_{\theta}}(s_t,a_t)\)的无偏但有噪声的估计。所以，我们可以用一个cirtic来代替它对action-value函数做估计，即

\[\color{green}{Q_{\mathbf{w}}(s,a) \approx Q^{\pi_{\theta}}(s,a)}\]

这样，更新就会变成

\[\nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}}\left[ \sum_{t=0}^{T-1} \color{green}{Q_{\mathbf{w}}(s,a)} \color{black}{\cdot} \nabla_{\theta} \log \pi_{\color{green}{\theta}} \color{black}{\left(a_{t} \mid s_{t}\right)} \right]\]

这样就得到了actor-critic policy gradient。

Actor：用于生成动作的策略函数
Critic：用于评估动作的奖励的价值函数

AC算法需要维护两组参数

Actor：按critic建议的方向更新策略参数\(\theta\)
Critic：更新动作-价值函数参数\(\mathbf{w}\)

5.4.2 Estimating the action-value function

Critic的作用是进行策略评估，即在当前的参数\(\theta\)下策略\(\pi_{\theta}\)有多好。策略评估是一个熟悉的问题，前面在Monte-Carlo policy evaluation、Temporal-Difference learning和Least-squares policy evaluation中都有探索过。

1. Action-value AC algorithm

利用一个线性值函数逼近器：\(Q_{\mathbf{w}}(s,a) = \psi(s,a)^T \mathbf{w}\)

Critic：根据线性的TD(0)来更新\(\mathbf{w}\)
Actor：根据策略梯度更新\(\theta\)

2. AC function approximators

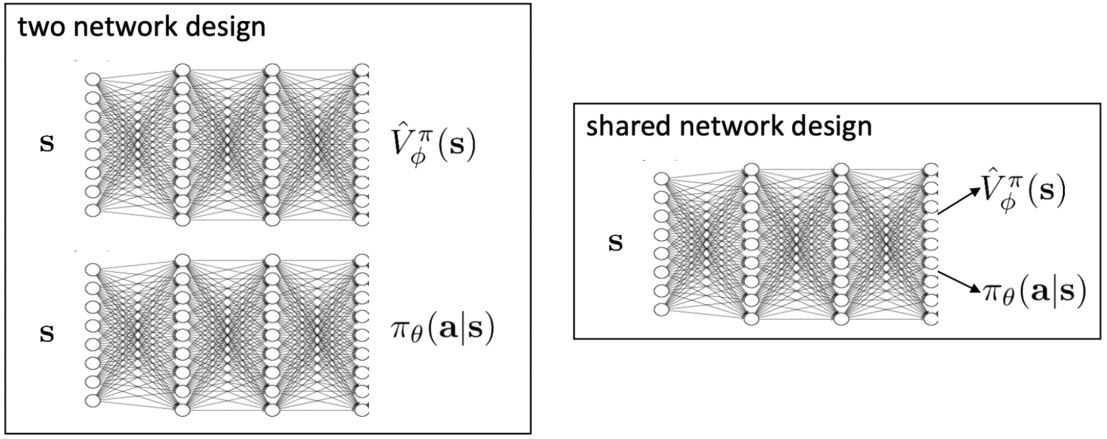
我们可以有两个独立的函数来逼近价值函数和策略函数，或者共用网络设计（特征提取是共享的，但输出有两个），如下图所示

5.4.3 Reducing the variance of AC by a baseline

还记得Q-funtion / state-action-value function为\(Q^{\pi, \gamma}(s,a) = \mathbb{E}_{\pi}[r_1 + \gamma r_2 + \ldots \mid s_1=s, a_1=a]\)。状态价值函数\(V^{\pi, \gamma}(s) = \mathbb{E}_{\pi}[r_1 + \gamma r_2 + \ldots \mid s_1=s] = \mathbb{E}_{a \sim \pi}[Q^{\pi, \gamma}(s,a)]\)就是一个很好的baseline。所以我们引入一个advantage function（优势函数），将\(Q\)和baseline \(V\)结合起来

\[\color{green}{ A^{\pi, \gamma}(s,a) = Q^{\pi, \gamma}(s,a) - V^{\pi, \gamma}(s) }\]

对应地，策略梯度变为

\[\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} [\nabla_{\theta} \log \pi_{\theta}(s,a) A^{\pi, \gamma}(s,a)]\]

5.4.4 N-step estimators

之前我们用的是reward的MC估计，我们也可以用TD方法来进行策略梯度的更新，或者其它任何TD和MC的混合方法。

对于\(n = 1, 2, \infty\)，n-step return为

\[\begin{array}{cl} n=1 \ (\text{TD}) \ \ & G_{t}^{(1)}=r_{t+1}+\gamma v\left(s_{t+1}\right) \\ n=2 \qquad \quad & G_{t}^{(2)}=r_{t+1}+\gamma r_{t+2}+\gamma^{2} v\left(s_{t+2}\right) \\ n=\infty(\text{MC}) & G_{t}^{(\infty)}=r_{t+1}+\gamma r_{t+2}+\ldots+\gamma^{T-t-1} r_{T} \end{array}\]

对应的advantage estimators为

\[\begin{aligned} \hat{A}_{t}^{(1)} &= r_{t+1}+\gamma v\left(s_{t+1}\right)-v\left(s_{t}\right) \\ \hat{A}_{t}^{(2)} &= r_{t+1}+\gamma r_{t+2}+\gamma^{2} v\left(s_{t+2}\right)-v\left(s_{t}\right) \\ \hat{A}_{t}^{(\infty)} &= r_{t+1}+\gamma r_{t+2}+\ldots+\gamma^{T-t-1} r_{T}-v\left(s_{t}\right) \end{aligned}\]

其中，\(\hat{A}_{t}^{(1)}\)方差低但偏差高，\(\hat{A}_{t}^{(\infty)}\)方差高但偏差低。

5.5 Overcoming Non-differentiable Computation

PG的另一个有趣的好处是它帮助我们克服了不可微计算。

在训练中，我们会生成很多样本（由下面的分支表示），然后我们将鼓励最终产生良好结果（在这种情况下，例如通过最后的损失来衡量）的样本。

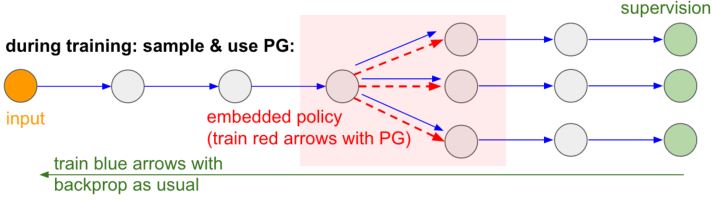
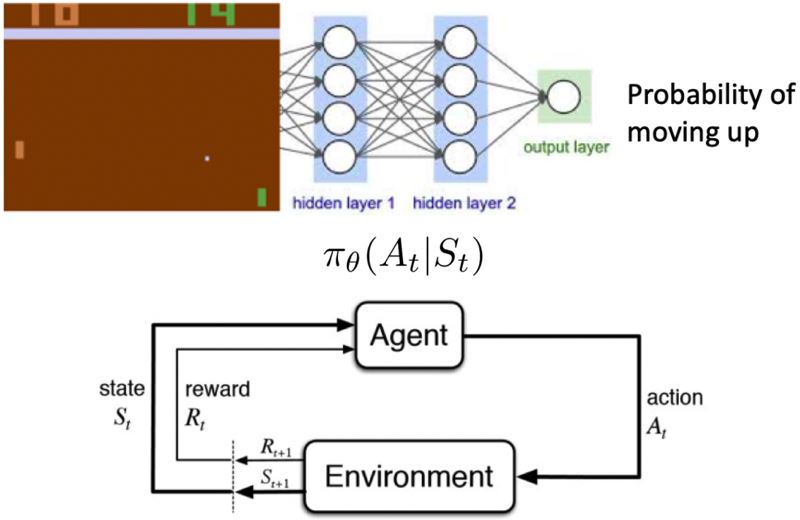
参考：Deep Reinforcement Learning: Pong from Pixels

Extention of Policy Gradient

目前最先进的强化学习方法几乎都是policy-based

A2C和A3C：Asynchronous Methods for Deep Reinforcement Learning, ICML'16. 具有代表性的高性能AC算法: https://openai.com/blog/baselines-acktr-a2c/
TRPO：Schulman, L., Moritz, Jordan, Abbeel (2015). Trust region policy optimization: deep RL with natural policy gradient and adaptive step size
PPO：Schulman, Wolski, Dhariwal, Radford, Klimov (2017). Proximal policy optimization algorithms: deep RL with importance sampled policy gradient

Different schools of RL

Value-based RL: 通过动态规划来解决RL
- 传统的强化学习和控制理论
- 代表性的算法：Deep Q-learning和它的变体
- 代表性的学者：Richard Sutton, David Silver, from DeepMind
Policy-based RL: 主要通过学习来解决RL
- 机器学习和深度学习
- 代表性的算法：PG和它的变体TRPO, PPO和其它的一些算法
- 代表性的学者：Pieter Abbeel, Sergey Levine, John Schulman, from OpenAI, Berkelely

详见周老师在知乎的回答：请问DeepMind和OpenAI身后两大RL流派有什么具体的区别？