Introduction

1.1 Classical and Modern Control

  现代控制理论主要解决多输入多输出（MIMO）问题，以一系列一阶differential (or difference) equation为基础。线性时不变系统（LTI）为

\[\begin{aligned} & \dot{\mathbf{x}}(t) = \mathbf{Ax}(t) + \mathbf{Bu}(t) \\ & \mathbf{y}(t) = \mathbf{Cx}(t) + \mathbf{Du}(t) \end{aligned}\]

类似地，非线性系统为

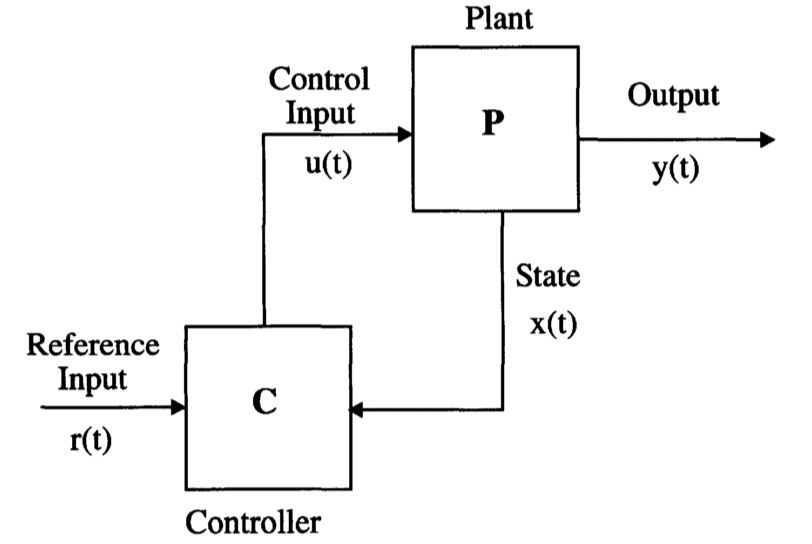
\[\begin{aligned} & \dot{\mathbf{x}}(t) = \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t),t) \\ & \mathbf{y}(t) = \mathbf{g}(\mathbf{x}(t),\mathbf{u}(t),t) \end{aligned}\] 现代理论认为，所有的状态变量都应在适当的加权后进行反馈。

  由图1.2可以看出，在modern control configuration中，

1.输入\(\mathbf{u}(t)\)由根据系统状态\(\mathbf{x}(t)\)和参考输入\(\mathbf{r}(t)\)驱动的控制器（由error detector和compensator）决定；
2.所有或大部分状态变量可控；
3.基于完善的矩阵理论，适合大规模的计算机仿真。

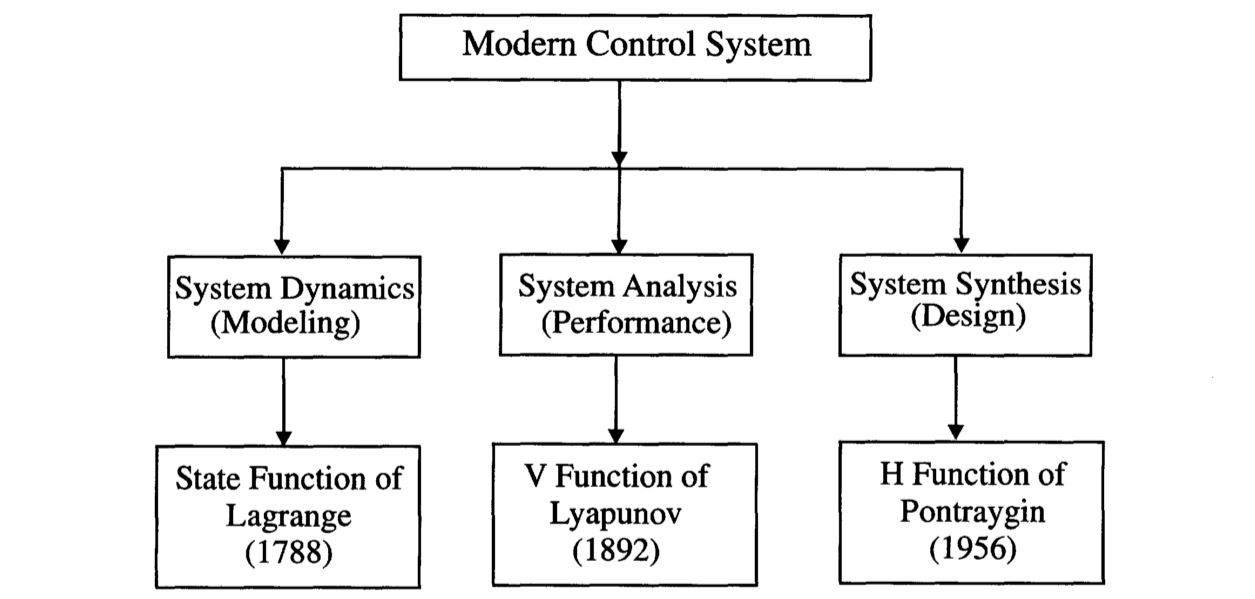
  现代控制系统的组成部分如图1.3所示。

1.2 Optimization

  如图1.4所示，变分法是优化领域的一小部分，它是学习最优控制系统的基础。

  优化可以进一步地分为静态优化和动态优化。
1.Static Optimization关注steady state条件下系统的控制，i.e.系统变量是时不变的。系统可以由代数方程表示，用的方法有：传统变分法、Lagrange乘数法、线性和非线性规划。
2.Dynamic Optimization关注dynamic条件下系统的最优控制，i.e.系统变量是时变的，因此系统描述与时间相关。系统由微分（或差分）方程描述，用的方法有搜索法、动态规划、变分法和Pontryagin原理。

1.3 Optimal Control

  最优控制的主要目标是找出使过程能满足某些物理约束，同时可以最大化或最小化某项性能标准（性能指标或成本函数）。

  最优控制问题的明确描述需要：
  1.被控系统的数学描述（或模型）（一般是状态空间表达式）；
  2.性能指标的确定；
  3.边界条件或状态和/或控制的物理约束的描述。

1.3.1 Plant

  出于优化的目的，我们用一系列线性或非线性微分（或差分）方程来描述一个物理设备。

1.3.2 Performance Index (PI)

  在现代控制理论中，最优控制问题是控制动态系统到达目标或跟随某个状态变量（或轨迹），并且同时最值化性能指标，可能有以下几种形式：

1.时间最优系统：在最短时间内，从任意的初始状态\(\mathbf{x}(t_0)\)到指定的最终状态\(\mathbf{x}(t_f)\)。相应的PI为

\[J = \int_{t_0}^{t_f} = t_f - t_0 = t^* \tag{1.3.1}\]

2.燃料最优系统：令\(u(t)\)为火箭引擎推力，假设推力大小\(\|u(t)\|\)与燃料消耗速率成比例。为了最小化燃料总支出，可以令PI为

\[J = \int_{t_0}^{t_f} |u(t)| dt \tag{1.3.2}\]

如果有多个控制量，可以写成

\[J = \int_{t_0}^{t_f} \sum_{i=1}^m {R_i |u_i(t)|} dt \tag{1.3.3}\]

其中，\(R\)为权重。

3.能量最优系统：电路的第i个回路的电流为\(u_i(t)\)，\(\sum_{i=1}^m u_i^2(t) r_i\)（其中，\(r_i\)是回路阻抗）为电路的总能量或能量的总消耗率。

\[J = \int_{t_0}^{t_f} \sum_{i=1}^m {u_i^2(t) r_i} dt \tag{1.3.4}\]

或者更一般的

\[J = \int_{t_0}^{t_f} {\mathbf{u}^T(t) \mathbf{R} \mathbf{u}(t) } dt \tag{1.3.5}\]

其中，\(\mathbf{R}\)是一个正定阵。

  类似地，考虑跟踪系统的平方误差最小化问题，有

\[J = \int_{t_0}^{t_f} {\mathbf{x}^T(t) \mathbf{Q} \mathbf{x}(t) } dt \tag{1.3.6}\]

其中，\(\mathbf{x}_d(t)\)为期望值，\(\mathbf{x}_a(t)\)为真实值，\(\mathbf{x}(t) = \mathbf{x}_a(t) - \mathbf{x}_d(t)\)为误差。这里的\(\mathbf{Q}\)是权重矩阵，可以是半正定的。

4.最终控制系统：最终误差为\(\mathbf{x}(t_f) = \mathbf{x}_a(t_f) - \mathbf{x}_d(t_f)\)。考虑误差的正负和权重系数，得到成本函数

\[J = \mathbf{x}^T(t_f) \mathbf{F} \mathbf{x}(t_f) \tag{1.3.7}\]

也可以叫terminal cost function。这里的\(\mathbf{F}\)是半正定矩阵。

5.一般的最优控制系统：结合以上几种情况，得到一般形式

\[J = \mathbf{x}^T(t_f) \mathbf{F} \mathbf{x}(t_f) + \int_{t_0}^{t_f} [\mathbf{x}^T(t) \mathbf{Q} \mathbf{x}(t) + \mathbf{u}^T(t) \mathbf{R} \mathbf{u}(t)] dt \tag{1.3.8}\]

或者

\[J = S(\mathbf{x}(t_f),t_f) + \int_{t_0}^{t_f} V \left( \mathbf{x}(t), \mathbf{u}(t), t\right) dt \tag{1.3.9}\]

其中，\(\mathbf{R}\)为正定阵，\(\mathbf{Q}\)和\(\mathbf{F}\)分别为半正定阵。Q、R可能是时变的。形如(1.3.8)的性能指标被称为二次型（quadratic）。

  最优控制问题是基于性能指标的形式进行分类的。如果PI包含\(S(\mathbf{x}(t),\mathbf{u}(t),t)\)，就是Mayer问题，如果PI只包含积分项，就是Lagrange问题，如果二者都有，就是Bolza问题。

1.3.2 Constraints

  控制向量\(\mathbf{u}t\)和状态向量\(\mathbf{x}t\)是否受限是由物理条件决定的，如

\[\mathbf{U}_+ \le \mathbf{u}(t) \le \mathbf{U}_- , \text{and} \quad \mathbf{X}_+ \le \mathbf{x}(t) \le \mathbf{X}_- \tag{1.3.10}\]

1.3.3 Formal Statement of Optimal Control System

  最优控制问题指的是找到最优控制\(\mathbf{u}^*t\)，使得线性时不变系统

\[\dot{\mathbf{x}}(t) = \mathbf{Ax}(t) + \mathbf{Bu}(t) \tag{1.3.11}\]

给出轨迹\(\mathbf{x}^*t\)，能优化或者最值化（最大值或最小值）性能指标

\[J = \mathbf{x}^T(t_f) \mathbf{F} \mathbf{x}(t_f) + \int_{t_0}^{t_f} [\mathbf{x}^T(t) \mathbf{Q} \mathbf{x}(t) + \mathbf{u}^T(t) \mathbf{R} \mathbf{u}(t)] dt \tag{1.3.12}\]

或者使非线性系统

\[\dot{\mathbf{x}}(t) = \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t),t) \tag{1.3.13}\]

给出状态\(\mathbf{x}^*t\)，能优化一般性能指标

\[J = S(\mathbf{x}(t_f),t_f) + \int_{t_0}^{t_f} V \left( \mathbf{x}(t), \mathbf{u}(t), t\right) dt \tag{1.3.14}\]

并且，控制变量\(\mathbf{u}t\)和/或状态变量\(\mathbf{x}t\)受(1.3.11)约束。最终时间\(t_f\)可以是固定的或自由的，最终状态可以是完全或半固定的或者自由的。整个问题描述如图1.5所示。

  最优控制系统的学习有三个阶段：

  1.考虑形如(1.3.14)的PI，用变分法求最优函数。

  2.引入(1.3.11)的系统，尝试解决形如(1.3.12)的PI的最优控制\(\mathbf{u}^*(t)\)。接着，在离散域讨论以上问题。

  3.在同时考虑约束和性能指标的情况下，找到最优控制。