Value Function Approximation
4.1 Introduction
4.1.1 Scaling up RL: VFA
对于大规模的强化学习问题,应该如何扩展无模型方法来进行预测和控制呢?
在表格型方法中,我们用一个查找表来表示价值函数。每个状态\(s\)都有一个条目\(V(s)\),每个状态-动作对\(s, a\)都有一个条目\(Q(s, a)\)。
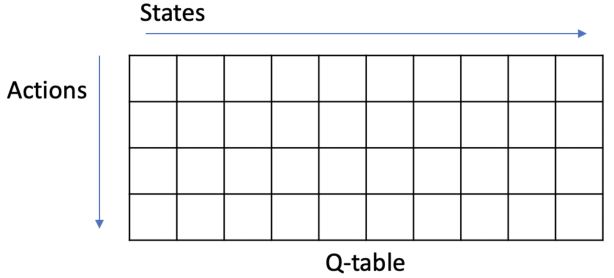
而在大规模的MDPs中,有过多的状态或动作需要存储,独立地学习每个状态的值所需的时间也过多,所以表格型算法无法解决。
问:如何避免为每个状态显式学习或存储以下内容呢?
- 动态或奖励模型
- 价值函数、状态-动作函数
- 策略
解:用函数近似来估计 \(\begin{aligned} \hat{v}(s,\mathbf{w}) & \approx v_{\pi}(s) \\ \hat{q}(s,a,\mathbf{w}) & \approx q_{\pi}(s,a) \\ \hat{\pi}(a,s,\mathbf{w}) & \approx \pi(a \vert s) \\ \end{aligned}\) ,从可见状态推广到不可见状态,用MC或TD学习来更新参数\(w\)。
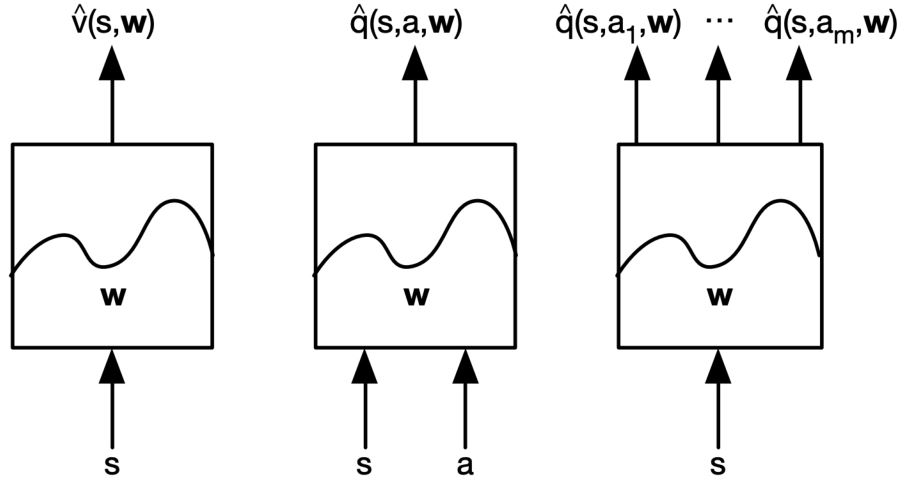
有很多可行的function approximators:
- 特征的线性结合
- 神经网络
- 决策树
- 最近邻居
本课程将聚焦可微的函数逼近器:linear feature representations和neural networks。
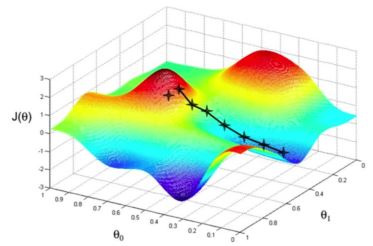
首先,我们来回顾一下梯度下降。函数\(J(\mathbf{w})\)是对参数向量\(\mathbf{w}\)可微,目标是找到能最小化\(J\)的参数\(\mathbf{w}^*\)。定义\(J(\mathbf{w})\)的梯度为
\[\nabla_{\mathbf{w}} J(\mathbf{w}) = \left[ \frac{\partial J(\mathbf{w})}{\partial w_1}, \frac{\partial J(\mathbf{w})}{\partial w_2}, \cdots, \frac{\partial J(\mathbf{w})}{\partial w_n} \right]^T\]向负梯度方向调整\(\mathbf{w}\),其\(\alpha\)为步长
\[\Delta \mathbf{w} = -\frac{1}{2} \alpha \nabla_{\mathbf{w}} J(\mathbf{w})\]Value Function Approximation with an Oracle:假设我们有一个预言可以知道任何给定状态\(s\)的真实价值\(v_{\pi}(s)\),目标是找到与\(v_{\pi}(s)\)最近似的表达。因此,使用均方误差并将损失函数定义为
\[J(\mathbf{w}) = \mathbb{E}_{\pi} \big[ (v_{\pi}(s) - \hat{v}(s,\mathbf{w}))^2 \big]\]沿着梯度下降找到一个局部最小值
\[\begin{aligned} \Delta \mathbf{w} &= -\frac{1}{2} \alpha \nabla_{\mathbf{w}} J(\mathbf{w}) \\ \mathbf{w}_{t+1} &= \mathbf{w}_t + \Delta \mathbf{w} \end{aligned}\]4.1.2 Linear VFA
用一个特征向量\(\mathbf{x}(s) = (x_1(s), \ldots, x_n(s))^T\)来表示状态
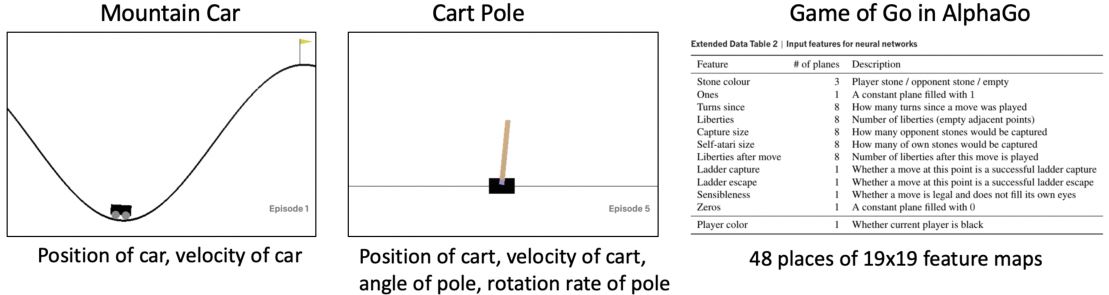
用特征的线性组合来表示价值函数
\[\hat{v}(s, \mathbf{w}) = \mathbf{x}(s)^T \mathbf{w} = \sum_{j=1}^n x_j(s) w_j\]目标函数中含\(\mathbf{w}\)的项是二次的
\[J(\mathbf{w}) = \mathbb{E}_{\pi} \big[ (v_{\pi}(s) - \mathbf{x}(s)^T \mathbf{w})^2 \big]\]因此更新规则很简单,\(\color{green}{\text{update} = \text{step size} \times \text{prediction error} \times \text{feature value}}\)
\[\Delta \mathbf{w} = \alpha[v_{\pi}(s) - \hat{v}(s,\mathbf{w})] \mathbf{x}(s)\]随机梯度下降会收敛到全局最优。因为在线性情况下,只有一个最优值,因此局部最优值会自动收敛到或接近全局最优值。
具有查表功能的线性值函数逼近:查表是线性值函数逼近的一种特殊情况。查表特征是one-hot vector(独热编码)
\[\mathbf{x}^{\text{table}}(s) = [1(s=s_1), \ldots, 1(s=s_n)]^T\]可以看到参数向量\(\mathbf{w}\)上的每个元素表示每个单独状态的值
\[\hat{v}(s, \mathbf{w}) = [1(s=s_1), \ldots, 1(s=s_n)][w_1, \ldots, w_n]^T\]因此,\(\hat{v}(s_k, \mathbf{w}) = w_k\)。
4.2 VFA for Prediction
实际上,对于任何状态\(s\),都无法获得关于\(v_{\pi}(s)\)真值的预言。
回顾一下无模型预测:
- 目标:评估按照某个固定策略\(\pi\)下的\(v_{\pi}\)
- 维护一个查找表来存储估计的\(v_{\pi}\)或\(q_{\pi}\)
- 估计值会在每个episode(MC法)或每步后更新(TD法)
因此,我们可以在循环中包含函数逼近步骤。
4.2.1 Incremental VFA prediction algorithms
假设实际的价值函数\(v_{\pi}(s)\)由某个监督者/预言给出
\[\Delta \mathbf{w} = \alpha[v_{\pi}(s) - \hat{v}(s,\mathbf{w})] \nabla_{\mathbf{w}} \hat{v}(s,\mathbf{w})\]但是,在强化学习中没有监督,只有奖励,所以在实际操作过程中,把\(v_{\pi}(s)\)替换成target。
对于MC,目标为实际return\(G_t\)
\[\Delta \mathbf{w} = \alpha[G_t - \hat{v}(s_t,\mathbf{w})] \nabla_{\mathbf{w}} \hat{v}(s_t,\mathbf{w})\]对于TD(0),目标为TD target \(R_{t+1} + \gamma \hat{v}(s_{t+1},\mathbf{w})\)
\[\Delta \mathbf{w} = \alpha[R_{t+1} + \gamma \hat{v}(s_{t+1},\mathbf{w}) - \hat{v}(s_t,\mathbf{w})] \nabla_{\mathbf{w}} \hat{v}(s_t,\mathbf{w})\]4.2.2 MC prediction with VFA
Return \(G_t\)是无偏的,而真值\(v_{\pi}(s_t)\)的采样是有噪声的。
问:为什么是无偏的?
因为\(\mathbb{E}[G_t] = v_{\pi}(s_t)\)
所以,我们有可用于VFA中监督学习的训练数据: \(<S_1,G_1>, <S_2,G_2>, \ldots <S_1,G_1>\)
利用线性Monte-Carlo策略评估
\[\begin{aligned} \Delta \mathbf{w} &= \alpha[G_t - \hat{v}(s_t,\mathbf{w})] \nabla_{\mathbf{w}} \hat{v}(s_t,\mathbf{w}) \\ &= \alpha[G_t - \hat{v}(s_t,\mathbf{w})] \mathbf{x}(s_t) \end{aligned}\]Monte-Carlo预测在线性和非线性价值函数近似中都是收敛的。
4.2.3 TD prediction with VFA
TD target \(R_{t+1} + \gamma \hat{v}(s_{t+1},\mathbf{w})\)是真值\(v_{\pi}(s_t)\)的有偏采样。
问:为什么有偏?
因为它来自之前的估计,而不是真值。\(\mathbb{E}[R_{t+1} + \gamma \hat{v}(s_{t+1},\mathbf{w})] \neq v_{\pi}(s_t)\)
所以,我们有可用于VFA中监督学习的训练数据: \(<S_1, R_2 + \gamma \hat{v}(s_2,\mathbf{w})>, <S_2, R_3 + \gamma \hat{v}(s_3,\mathbf{w})>, \ldots <S_{T-1}, R_T>\)
利用线性TD(0),随机梯度下降更新为
\[\begin{aligned} \Delta \mathbf{w} &= \alpha[R + \gamma \hat{v}(s',\mathbf{w}) - \hat{v}(s,\mathbf{w})] \nabla_{\mathbf{w}} \hat{v}(s_t,\mathbf{w}) \\ &= \alpha[R + \gamma \hat{v}(s',\mathbf{w}) - \hat{v}(s,\mathbf{w})] \mathbf{x}(s) \end{aligned}\]这也称为semi-gradient,因为忽略了改变权重向量\(\mathbf{w}\)对目标的影响。
线性TD(0)会收敛(靠近)全局最优。
4.3 VFA for Control
广义策略迭代(GPI)
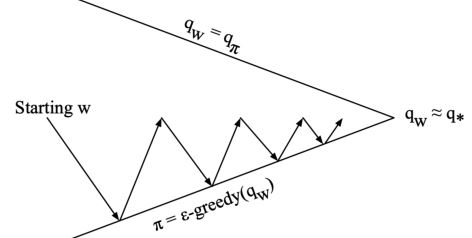
- 策略评估:近似策略评估,\(\hat{q}(., ., \mathbf{w}) \approx q_{\pi}\)
- 策略改进:\(\epsilon\)-贪心策略改进
4.3.1 Action-value function approximation
近似动作-价值函数
\[\hat{q}(s, a, \mathbf{w}) \approx q_{\pi}(s, a)\]最小化近似动作价值与真实动作价值之间的均方误差(mean-square error, MSE)
\[J(\mathbf{w}) = \mathbb{E}_{\pi} [(q_{\pi}(s, a) - \hat{q}(s, a, \mathbf{w}))^2]\]通过随机梯度下降,找到一个局部极小值
\[\Delta \mathbf{w} = \alpha[q_{\pi}(s, a) - \hat{q}(s, a, \mathbf{w})] \nabla_{\mathbf{w}} \hat{q}(s, a, \mathbf{w})\]进一步地,考虑线性动作-价值函数近似。用特征向量表示状态和动作
\[\mathbf{x}(s, a) = \big( x_1(s, a), \ldots, x_n(s, a) \big)^T\]用特征的线性组合表示动作-价值函数
\[\hat{q}(s, a, \mathbf{w}) = \mathbf{x}(s, a)^T \mathbf{w} = \sum_{j=1}^n x_j(s,a) w_j\]因此,随机梯度下降更新为
\[\Delta \mathbf{w} = \alpha[q_{\pi}(s, a) - \hat{q}(s, a, \mathbf{w})] \mathbf{x}(s, a)\]4.3.2 Incremental control algorithm
与预测一样,关于\(q_{\pi}(s,a)\)真值的预言是不存在的,所以把它换成target
对于MC,目标为实际return\(G_t\)
\[\Delta \mathbf{w} = \alpha[G_t - \hat{q}(s_t, a_t, \mathbf{w})] \nabla_{\mathbf{w}} \hat{q}(s_t, a_t, \mathbf{w})\]对于Sarsa,目标为TD target \(R_{t+1} + \gamma \hat{q}(s_{t+1}, a_{t+1}, \mathbf{w})\)
\[\Delta \mathbf{w} = \alpha \big[R_{t+1} + \gamma \hat{q}(s_{t+1}, a_{t+1}, \mathbf{w}) - \hat{q}(s_t, a_t, \mathbf{w}) \big] \nabla_{\mathbf{w}} \hat{q}(s_t, a_t \mathbf{w})\]对于Q-learning,目标为TD target \(R_{t+1} + \gamma \max_a \hat{q}(s_{t+1}, a, \mathbf{w})\)
\[\Delta \mathbf{w} = \alpha \big[R_{t+1} + \gamma \max_a \hat{q}(s_{t+1}, a_{t+1}, \mathbf{w}) - \hat{q}(s_t, a_t, \mathbf{w}) \big] \nabla_{\mathbf{w}} \hat{q}(s_t, a_t \mathbf{w})\]
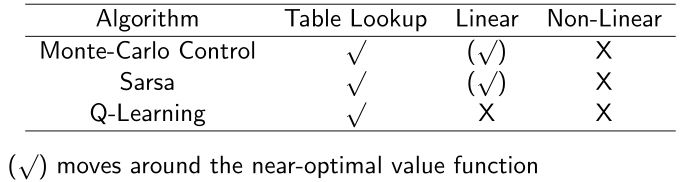
4.3.3 Convergence of control methods with VFA
- 对于Sarsa,\(\Delta \mathbf{w} = \alpha \big[R_{t+1} + \gamma \hat{q}(s_{t+1}, a_{t+1}, \mathbf{w}) - \hat{q}(s_t, a_t, \mathbf{w}) \big] \nabla_{\mathbf{w}} \hat{q}(s_t, a_t \mathbf{w})\)
- 对于Q-learning,\(\Delta \mathbf{w} = \alpha \big[R_{t+1} + \gamma \max_a \hat{q}(s_{t+1}, a_{t+1}, \mathbf{w}) - \hat{q}(s_t, a_t, \mathbf{w}) \big] \nabla_{\mathbf{w}} \hat{q}(s_t, a_t \mathbf{w})\)
采用VFA的TD没有沿着任何一个目标函数的梯度,更新过程通过通过拟合底层价值函数包含了近似Bellman回溯过程。因此,TD在使用离轨策略或者非线性函数近似时会发散。离轨控制的挑战性在于行为策略和目标策略不相同,因此价值函数近似会发散。
导致不稳定和发散的三个致命要素:(详见课本11.3节)
- 函数近似:一种从比内存和计算资源大得多的状态空间进行泛化的可扩展方式
- 自举:更新包含现有估计的目标(如DP或TD方法),而不是完全依赖实际奖励和完全回报(如MC方法)
- 离轨试验:对目标策略产生的转移分布以外的分布进行训练
4.4 Least Square P & C: Batch RL
增量梯度更新易于实现,但是不能有效采样。基于批量的方法试图为大量的agent的经验找到最贴合的价值函数。
4.4.1 Least square prediction
给定价值函数近似\(\hat{v}(s, \mathbf{w}) \approx v_{\pi}(s)\)。经验\(\mathcal{D}\)由<状态,价值>组成(可能从一次episode或很多先前的episodes得来),\(\mathcal{D} = \{ <s_1, v_1^{\pi}>, \ldots, <s_t, v_T^{\pi}> \}\)
目标:优化参数\(\mathbf{w}\)来更好地符合经验\(\mathcal{D}\)
采用最小二乘算法最小化\(\hat{v}(s_t, \mathbf{w})\)与目标值\(v^{\pi}_t\)之间的平方和误差\(\begin{aligned} \mathbf{w}^* =& \text{arg} \min_{\mathbf{w}} \mathbb{E}_{\mathcal{D}} [(v_{\pi} - \hat{v}(s, \mathbf{w}))^2] \\=& \text{arg} \min_{\mathbf{w}} \sum_{t=1}^T (v^{\pi}_t - \hat{v}(s_t, \mathbf{w}))^2\end{aligned}\)
4.4.2 Stochastic gradient descent with experience repaly
给定由<状态,价值>组成的经验\(\mathcal{D} = \{ <s_1, v_1^{\pi}>, \ldots, <s_t, v_T^{\pi}> \}\),迭代解为以下两个步骤的重复
- 从经验中随机采样一个<状态,价值>对,\(<s_, v_{\pi}> \sim \mathcal{D}\)
- 应用随机梯度下降更新\(\Delta \mathbf{w} = \alpha (v_{\pi} - \hat{v}(s, \mathbf{w})) \nabla_{\mathbf{w}} \hat{v}(s, \mathbf{w})\)
梯度下降法的解收敛于最小二乘解\(\mathbf{w}^{LS} = \text{arg}\min_{\mathbf{w}} \sum_{t=1}^T (v^{\pi}_t - \hat{v}(s_t, \mathbf{w}))^2\)
4.5 Deep Q-learning
将强化学习推广到解决实际问题,如自动驾驶汽车、雅达利、消费者营销、医疗保健、教育……这些实际问题大多有非常大的状态和/或操作空间,需要能够将模型/价值/策略概括在状态和/或动作内的表示方法。解决方案:用参数函数来表示一个值函数,而不是一个查找表。
\[\begin{aligned} \hat{v}(s, \mathbf{w}) & \approx v_{\pi}(s) \\ \hat{q}(s, a, \mathbf{w}) & \approx q_{\pi}(s, a) \end{aligned}\] 用特征的线性组合来表示价值函数\(\hat{v}(s, \mathbf{w}) = \mathbf{x}(s)^T \mathbf{w} = \sum_{j=1}^n x_j(s) w_j\),目标函数为\(J(\mathbf{w}) = \mathbb{E}_{\pi} \big[ (v_{\pi}(s) - \mathbf{x}(s)^T \mathbf{w})^2 \big]\)。更新规则很简单,\(\Delta \mathbf{w} = \alpha[v_{\pi}(s) - \hat{v}(s,\mathbf{w})] \mathbf{x}(s)\)。但是,实际上并不存在关于真值\(v_{\pi}(s)\)的预言,所以用MC或TD的target来替代。
对于MC策略评估,\(\Delta \mathbf{w} = \alpha[G_t - \hat{v}(s_t,\mathbf{w})] \mathbf{x}(s_t)\)
对于TD策略评估,\(\Delta \mathbf{w} = \alpha [R_{t+1} + \gamma \hat{v}(s_{t+1},\mathbf{w}) - \hat{v}(s_t,\mathbf{w})] \mathbf{x}(s_t)\)
Linear vs nonlinear VFA:
- 线性VFA通常在适当的特征集下工作得很好,但需要人为设计特征集。
- 另一种选择是使用一个更丰富的函数近似器,它能够直接从状态中学习,而不需要特征设计
- 非线性函数近似器:深度神经网络
4.5.1 Deep neural networks
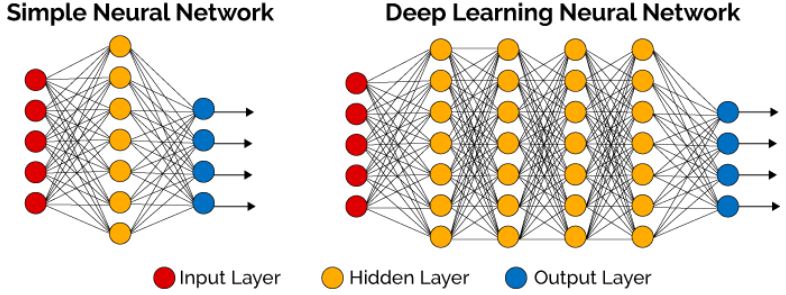
深度神经网络有多层线性函数,层与层之间有非线性算子
\[f(\mathbf{x}; \theta) = \mathbf{W}_{L+1}^T \sigma \big( \mathbf{W}_L^T \sigma \big( \ldots \sigma \mathbf{W}_1^T \mathbf{x} + \mathbf{b}_1) + \ldots + \mathbf{b}_{L-1} \big) + \mathbf{b}_L \big) \mathbf{b}_{L+1}\]根据链式法则,进行梯度反向传播来更新权重,利用loss function \(L(\theta) = \frac{1}{n} \sum_{i=1}^n [(y^{(i)} - f(\mathbf{x}; \theta)]^2\)。
深度强化学习处于机器学习和人工智能的前沿。深度神经网络可以用来表示价值函数、策略函数(后面将介绍策略梯度方法)、世界模型等。损失函数是用随机梯度下降(SGD)优化的。
存在的挑战有:
- 效率:需要优化的模型参数太多
- 导致训练不稳定性和发散的致命三角(非线性函数近似、自举、离轨策略训练)
4.5.2 Deep Q-networks (DQN)
DeepMind's Nature paper: Mnih, Volodymyr; et al. (2015). Human-level control through deep reinforcement learning. DQN利用神经网络近似器来表示动作价值函数。DQN使用相同的网络和超参数,在许多雅达利游戏中达到了专业的人类游戏水平。 、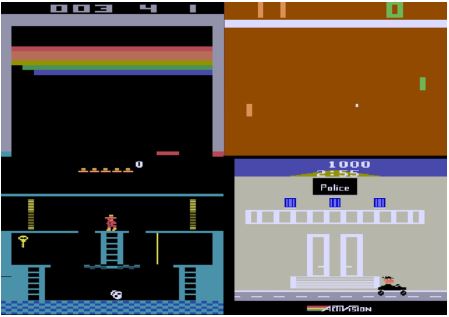
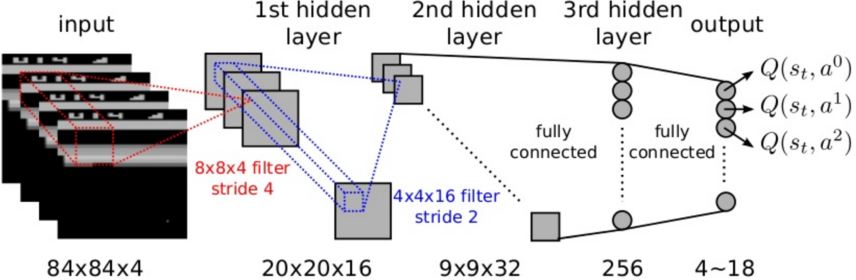
用于雅达利游戏的DQN
- 根据输入像素帧来端对端地学习\(Q(s,a)\)的值
- 输入状态\(s\)是最近4帧的原始像素堆栈
- 输出\(Q(s,a)\)是18个操控杆/按钮位置
- 奖励是每步后得分的变化
- 所有游戏的网络结构和超参数都是固定的
利用价值函数近似的Q-learning有两点可能引发问题:
- 样本之间的相关性
- 非静态目标
DQN解决这些问题的方法:1. 经验回放 2. 固定Q targets
DQNs: experience replay
为了减弱样本之间的相关性,将转移过程\((s_t, a_t, r_t, s_{t+1})\)存储到经验池\(\mathcal{D}\)中
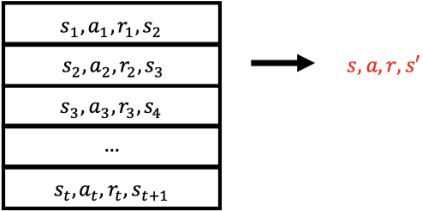
重复以下步骤,实现经验回放:
- 从数据集中采样一个经验元:\((s, a, r, s') \sim \mathcal{D}\)
- 计算被采样的tuple的目标值:\(r + \gamma \max_{a'} \hat{Q}(s', a', \mathbf{w})\)
- 利用随机梯度下降更新网络权值\(\Delta \mathbf{w} = \alpha \big( r + \gamma \max_{a'} \hat{Q}(s', a', \mathbf{w}) - Q(s, a, \mathbf{w}) \big) \nabla_{\mathbf{w}} \hat{Q}(s, a, \mathbf{w})\)
DQNs: fixed targets
