Trust Region Policy Optimization

A Natural Policy Gradient Kakade, 2001
Trust region policy optimization. Schulman, L., Moritz, Jordan, Abbeel. 2015

参考：techblog: Natural Gradient Descent
   知乎：自然策略梯度

1 Natural Policy Gradient

  标准梯度下降\(\pmb{\theta}_{k+1} = \pmb{\theta}_k - \alpha_k \nabla J(\pmb{\theta}_k)\)无法保证目标函数\(J(\pmb{\theta})\)按最大速度下降，因为标准梯度下降是非协变的 (non-covariant)，\(\pmb{\theta}\)的参数空间不是欧几里得的。一般来说参数空间具有黎曼度量结构，如神经网络。在这些情况下，普通梯度不能给出目标函数最陡峭的方向，所以A Natural Policy Gradient一文提出了能够实现参数空间最速下降的自然梯度。

1.1 Riemannian Space

  欧式空间具有标准正交坐标系，其微分向量的平方长度为\(\vert d w \vert^2 = \sum_{i=1}^n (d w_i)^2\)。而黎曼空间是一种矢量空间，不具有正交坐标系，其微分向量的平方长度由正定二次型决定

\[\vert d \boldsymbol{w} \vert^2 = \sum_{i,j} \mathbf{G} dw_i dw_j\]

其中\(\mathbf{G}\)是一个\(n * n\)的对称矩阵。当\(\mathbf{G}\)为单位对角阵\(\mathbf{I}\)时，黎曼空间退化为欧氏空间。

  黎曼空间中最速下降的梯度为

\[\tilde{\nabla} L(\boldsymbol{w}) = \mathbf{G}^{-1}(\boldsymbol{w}) \nabla L(\boldsymbol{w})\]

其中\(G\)可以用Fisher信息矩阵\(F\)替换。【证明】

  似然函数\(L(\theta \mid x) = f_{\theta}(x) = f(\theta \mid x)\) (\(L(\theta \mid x) = p(X = x; \theta) = p_{\theta}(x)\))，对数似然函数为\(s(\theta) = \nabla_{\theta} \log p(x \mid \theta)\)，其Fisher矩阵为

\[\mathbf{F} = \mathbb{E}_{p(x \mid \theta)}[\nabla \log p(x \mid \theta) \nabla \log p(x \mid \theta)^T]\]

1.2 A Natural Gradient

  一个有限MDP可以描述为\((S, s_0, A, R, P)\)，agent的决策根据随机策略\(\pi (a; s)\)。假设每个策略\(\pi\)有静态分布\(\rho^{\pi}\)，那么average reward（或undiscounted reward）为

\[\eta(\pi) \equiv \sum_{s, a} \rho^\pi(s) \pi(a; s) R(s, a)\]

state-action值为

\[Q^\pi(s, a) \equiv E_\pi \left\{ \sum_{t=0}^{\infty} R\left(s_t, a_t\right) - \eta(\pi)\mid s_0=s, a_0=a \right\}\]

value funtion为

\[J^{\pi} \equiv E_{\pi(a';s)} \{ Q^\pi(s, a') \}\]

  考虑更复杂的情况，目标是找到一个能最大化平均奖励的策略且该策略是平滑参数化的，\(\tilde{\Pi} = \left\{ \pi_\theta: \theta \in \Re^m \right\}\)，其中\(\pi_\theta\)表示\(\pi(a; s, \theta)\)。

  那么平均奖励的精确梯度为

\[\nabla \eta(\theta) = \sum_{s, a} \rho^\pi(s) \nabla \pi(a; s, \theta) Q^\pi(s, a)\]

其中，我们用\(\eta(\theta)\)来简写\(\eta(\pi_{\theta})\)。

  最速下降方向向量为\(d \theta\)，其平方长度为\(\vert d \theta \vert^2 = \sum_{i,j} G_{i,j} d \theta_i d \theta_j = d \theta^T G(\theta) d \theta\)，所以最速下降的方向为\(G^{-1} \nabla \eta(\theta)\)。对于每个状态\(s\)都有一个对应的概率流形，分布\(\pi(a; s, \theta)\)是坐标系为\(\theta\)的流形上的一点。分布\(\pi(a; s, \theta)\)的Fisher信息矩阵为

\[F_s(\theta) \equiv \mathbb{E}_{\pi(a; s, \theta)} \left[ \frac{\partial \log \pi(a ; s, \theta)}{\partial \theta_i} \frac{\partial \log \pi(a ; s, \theta)}{\partial \theta_j} \right]\]

Fisher信息矩阵在一定程度上是概率分布参数空间上的不变度量，因为用它定义的距离与坐标系的选择（即参数化）如何无关。

  由于平均奖励是在这些分布的集合上定义的，我们为度量做出的直接选择是

\[\color{green}{ F(\theta) \equiv \mathbb{E}_{\rho^{\pi}}[F_s(\theta)] }\]

其中期望与\(\pi_{\theta}\)的静态分布有关。值得注意的是，虽然每个\(F_s\)独立于MDP转移模型的参数，但是静态分布的权重引入了对这些参数的依赖性。

  最终得到的自然梯度为

\[\color{green}{ \widetilde{\nabla} \eta(\theta) \equiv F(\theta)^{-1} \nabla \eta(\theta) }\]

2 Trust Region Policy Optimization

  一种优化控制策略的方法，可保证单调改进。通过对理论上合理的方案进行一些近似，开发了一种实用的算法，称为信任区域策略优化 (TRPO)。该方法对优化更大的非线性策略有效，比如神经网络。尽管其近似偏离了理论，但是TRPO倾向于给出单调改进，且几乎不需要调整超参数。

2.1 Preliminaries

  无限MDP表示为\((\mathcal{S}, \mathcal{A}, P, c, \rho_0, \gamma)\)，其中\(P: \mathcal{S} \times \mathcal{A} \times \mathcal{S}\)为转移概率分布，\(c\)为cost，\(\rho_0\)为初态\(s_0\)的概率分布。随机策略为\(\pi : \mathcal{S} \times \mathcal{A}\)。

  期望折扣cost为

\[\begin{aligned} & \eta(\pi) = \mathbb{E}_{s_0, a_0, \ldots} \left[ \sum_{t=0}^{\infty} \gamma^t c (s_t) \right], \\ & \text { where } s_0 \sim \rho_0\left(s_0\right), a_t \sim \pi\left(a_t \mid s_t\right), s_{t+1} \sim P\left(s_{t+1} \mid s_t, a_t\right) \end{aligned}\]

  state-action value function \(Q_\pi\)，value function \(V_\pi\)和advantage function \(A_\pi\)分别为

\[\begin{aligned} & Q_\pi (s_t, a_t) = \mathbb{E}_{s_{t+1}, a_{t+1}, \ldots} \left[\sum_{l=0}^{\infty} \gamma^l c (s_{t+l}) \right], \\ & V_\pi t(s_t) = \mathbb{E}_{a_t, s_{t+1}, \ldots} \left[ \sum_{l=0}^{\infty} \gamma^l c (s_{t+l}) \right], \\ & A_\pi (s, a) = Q_\pi(s, a)-V_\pi(s), \\ & \text { where } a_t \sim \pi (a_t \mid s_t), s_{t+1} \sim P\left(s_{t+1} \mid s_t, a_t\right) \text { for } t \geq 0 . \end{aligned}\]

  策略\(\tilde{\pi}\)的期望折扣cost \(\eta\)，用\(\pi\)的adavantage函数表示为

\[\begin{aligned} & \eta(\tilde{\pi}) = \eta(\pi) + \mathbb{E}_{s_0, a_0, s_1, a_1, \ldots} \left[ \sum_{t=0}^{\infty} \gamma^t A_\pi (s_t, a_t) \right], \\ & \text { where } s_0 \sim \rho_0 (s_0), a_t \sim \tilde{\pi} (a_t \mid s_t), s_{t+1} \sim P (s_{t+1} \mid s_t, a_t) \end{aligned} \tag{1}\]

  令\(\rho_\pi\)为(非归一化的)折扣访问频率

\[\rho_\pi(s) = \left( P(s_0=s)+\gamma P(s_1=s)+\gamma^2 P(s_2=s)+\ldots \right)\]

把(1)改写为按状态求和，得到

\[\eta(\tilde{\pi}) = \eta(\pi) + \sum_s \rho_{\tilde{\pi}}(s) \sum_a \tilde{\pi}(a \mid s) A_\pi(s, a) \tag{2}\]

表明每次策略更新\(\pi \rightarrow \tilde{\pi}\)时，对于所有状态\(s\)都有非正的期望advantage，即\(\sum_a \tilde{\pi}(a \mid s) A_\pi(s, a) \le 0\)必能让\(\eta\)变小。当用确定性策略\(\tilde{\pi}(s) = \operatorname{arg} \min_a A_{\pi}(s, a)\)更新时，当至少有一个state-action的\(A\)为负且有非零访问概率时，才会改进策略。但是，由于估计和近似误差的存在，无法保证\(A \le 0\)。并且\(\rho_{\tilde{\pi}}(s)\)与\(\tilde{\pi}\)的关系复杂，所以(2)无法直接优化。

  对\(\eta(\tilde{\pi})\)作局部近似，用\(\rho_\pi\)代替\(\rho_{\tilde{\pi}}\)，得到

\[\color{green}{\boxed{ L_{\pi}(\tilde{\pi}) = \eta(\pi) + \sum_s \rho_{\pi}(s) \sum_a \tilde{\pi}(a \mid s) A_\pi(s, a) }}\tag{3}\]

对于参数化策略\(\pi_{\theta}\)，若\(\pi_{\theta}(a \mid s)\)关于\(\theta\)可微，那么\(L_{\pi}\)符合\(\eta\)的一阶等效，即二者关于\(\theta\)的梯度相等。

How big a step?
— 保守策略迭代 (conservative policy iteration)，给出\(\eta\)改进的明确下界。

  当前策略为\(\pi_{\text{old}}\)，假设可解\(\pi' = \operatorname{arg} \min_{\pi'} L_{\pi_{\text{old}}} (\pi')\)。新策略采用以下混合策略：

\[\pi_{\text {new }}(a \mid s) = (1-\alpha) \pi_{\text {old }}(a \mid s)+\alpha \pi^{\prime}(a \mid s) \tag{5}\]

Kakade and Langford为该更新证明了以下结果：

\[\eta (\pi_{\text {new }}) \le L_{\pi_{\text{old}}}(\pi_{\text {new }}) + \frac{2 \epsilon \gamma}{(1-\gamma(1-\alpha))(1-\gamma)} \alpha^2 \tag{6}\]

其中，\(\epsilon\)是\(\pi'\)关于\(\pi\)的最大advantage（正或负）

\[\epsilon = \max _s \left|\mathbb{E}_{a \sim \pi^{\prime}(a \mid s)}\left[A_\pi(s, a)\right] \right|\]

由于\(\alpha, \gamma \in [0, 1]\)，(6)意味着以下更简单的界限

\[\eta (\pi_{\text {new }}) \le L_{\pi_{\text{old}}}(\pi_{\text {new }}) + \frac{2 \epsilon \gamma}{(1-\gamma)^2} \alpha^2 \tag{8}\]

此界限仅在\(\alpha \ll 1\)时略弱，Kakade & Langford (2002)的保守策略迭代方法通常就是这种情况。此界限只适用于(5)生成的混合策略，该策略再实践中笨拙且受限，所以我们期望能有个实用的策略更新方案，能够适用于所以一般随机策略类型。

2.2 Monotonic Improvement Guarantee for General Stochastic Policies

  主要理论成果：通过用\(\pi\)和之间的\(\tilde{\pi}\)的距离代替\(\alpha\)，将由(6)约束的策略改进推广到一般随机策略，而非仅仅是混合策略。

  距离度量采用总二分散度 (total variation divergence)。离散概率分布\(p, q\)之间的总二分散度为\(D_{\text{TV}} (p \| q) = \frac{1}{2} \sum_i \vert p_i - q_i \vert\)，定义

\[D_{\text{TV}}^{\max}(\pi, \tilde{\pi}) = \max_s D_{\text{TV}} \big( \pi(\cdot \mid s) \| \tilde{\pi}(\cdot \mid s) \big)\]

Theorem 1. 令\(\alpha = D_{\text{TV}}^{\max}(\pi_{\text{old}}, \pi_{\text{new}})\)，且令\(\epsilon = \max_s \vert \mathbb{E}_{a \sim \pi^{\prime}(a \mid s)} [A_{\pi}(s, a)] \vert\)，那么(8)成立。

  由于\(D_{\text{TV}} (p \| q)^2 \le D_{\text{KL}} (p \| q)\)，令\(D_{\text{KL}}^{\max}(\pi, \tilde{\pi}) = \max_s D_{\text{KL}} \big( \pi(\cdot \mid s) \| \tilde{\pi}(\cdot \mid s) \big)\)，那么由(8)可得

\[\color{green}{\boxed{ \eta(\tilde{\pi}) \le L_\pi(\tilde{\pi}) + C D_{\mathrm{KL}}^{\max }(\pi, \tilde{\pi}), \text { where } C = \frac{2 \epsilon \gamma}{(1-\gamma)^2} }}\tag{10}\]

注意，从这里开始，我们假设adavantage values \(A_{\pi}\)的精确评估。

  下面提出的TRPO将是Alg 1的近似，TRPO通过对KL散度的约束而非惩罚来稳健地允许大的更新。

2.3 Optimization of Parameterized Policies

  前面考虑的都是与\(\pi\)的参数化无关的策略优化问题，并且基于所有状态下的策略都可以被评估的假设。下面将描述如何得到根据以上理论基础得到一个实用的算法，在有限采样次数和任意参数化下都实用。

  考虑参数化的策略\(\pi_{\theta}(a \mid s)\)，其参数为\(\theta\)，所以用\(\theta\)来重载之前\(\pi\)的函数。用\(\theta_{\text{old}}\)来表示我们希望改进的旧策略的参数。
  前面推导出\(\eta(\theta) \le L_{\theta_{\text{old}}} + C D_{\mathrm{KL}}^{\max }(\theta_{\text{old}}, \theta)\)，且在\(\theta = \theta_{\text{old}}\)时取等号。因此通过求以下最小值，可以保证改进真是目标\(\eta\)。

\[\min_{\theta} [L_{\theta_{\text{old}}} + C D_{\mathrm{KL}}^{\max }(\theta_{\text{old}}, \theta)]\]

  在实际操作中，如果用罚系数\(C\)，步长会非常小。一个比较稳健的采用更大的步长的方法是在新策略和旧策略间的KL散度上加一个约束，i.e. a trust region constraint:

\[\begin{aligned} &\min_{\theta} L_{\theta_{\mathrm{old}}}(\theta) \\ &\text { s.t. } D_{\mathrm{KL}}^{\max }\left(\theta_{\mathrm{old}}, \theta\right) \leq \delta \end{aligned}\]

但是，因为约束的量太多（状态空间的每个点上的KL散度都受限）所以这个问题不好解。可以用考虑了平均KL散度的启发式近似方法：

\[\bar{D}_{\mathrm{KL}}^\rho\left(\theta_1, \theta_2\right) := \mathbb{E}_{s \sim \rho} \bigg[ D_{\mathrm{KL}}\big(\pi_{\theta_1}(\cdot \mid s) \| \pi_{\theta_2}(\cdot \mid s)\big) \bigg]\]

因此，提出通过解以下优化问题来生成策略更新：

\[\color{green}{\boxed{\begin{aligned} &\min_{\theta} L_{\theta_{\mathrm{old}}}(\theta) \\ &\text { s.t. } \bar{D}_{\mathrm{KL}}^{\max }\left(\theta_{\mathrm{old}}, \theta \right) \leq \delta \end{aligned}}} \tag{13}\]

2.4 Sample-Based Estimation of the Objective and Constraint

  这节主要介绍如何用Monte Carlo simulation来近似目标函数和约束函数。

  将(13)中\(L_{\theta_{\mathrm{old}}}(\theta)\)展开，得到以下优化问题：

\[\begin{aligned} \min_{\theta} & \sum_s \rho_{\theta_{\text {old }}}(s) \sum_a \pi_\theta(a \mid s) A_{\theta_{\text {old }}}(s, a) \\ \text {s.t. } & \bar{D}_{\mathrm{KL}}^{\rho_{\theta_{\text{old}}}} (\theta_{\text {old }}, \theta) \le \delta \end{aligned}\]

首先，用期望\(\frac{1}{1 - \gamma} \mathbb{E}_{s \sim \rho_{\theta_{\text{old}}}} [\cdots]\)代替\(\sum_s \rho_{\theta_{\text {old }}}(s) [\cdots]\)。然后用Q-values \(Q_{\theta_{\text {old}}}\)代替\(A_{\theta_{\text {old}}}\)。最后，用重要性采样代替对action的求和。用\(q\)表示采样分布，单个\(s_n\)对损失函数的贡献为

\[\sum_a \pi_\theta (a \mid s_n) A_{\theta_{\text{old}}}(s_n, a) = \mathbb{E}_{a \sim q} \left[ \frac{\pi_\theta (a \mid s_n)}{q(a \mid s_n)} A_{\theta_{\text {old }}}\left(s_n, a\right) \right]\]

把(14)写成如下期望的形式

\[\begin{aligned} \min_{\theta} \ & \mathbb{E}_{s \sim \rho_{\theta_{\text{old}}}, a \sim q}\left[\frac{\pi_\theta(a \mid s)}{q(a \mid s)} Q_{\theta_{\text{old}}}(s, a)\right] \\ \text {s.t.} \ & \mathbb{E}_{s \sim \rho_{\theta_{\text{old}}}}\left[D_{\mathrm{KL}}\left(\pi_{\theta_{\text {old }}}(\cdot \mid s) \| \pi_\theta(\cdot \mid s)\right)\right] \leq \delta \end{aligned}\]

  剩下的就是用样本均值代替预期，用经验估计代替Q值。下面将介绍两种不同的估计方案。

2.4.1 Single path

  在这个估计过程中，通过采样\(s_0 \sim \rho_0\)收集状态序列，然后模拟策略\(\pi_{\theta_{\text{old}}}\)对一些时间步长生成轨迹\(s_0, a_0, a_1, a_1, \ldots, s_{T-1}, a_{T-1}, s_T\)。因此，\(q(a \vert s) = \pi_{\theta_{\text{old}}} (a \vert s)\)。通过沿轨迹取未来成本的折扣和可以得到每个state-action的\(Q_{\theta_{\text{old}}} (s, a)\)。

2.4.2 Vine

  在这个估计过程中，首先采样\(s_0 \sim \rho_0\)并仿真策略\(\pi_{\theta_i}\)来生成一些轨迹。然后沿着这些轨迹选一个子集表示为\(s_1, s_2, \ldots, s_N\)，称为"rollout set"。对rollout set中每个状态\(s_n\)，我们根据\(a_{n, k} \sim q(\cdot \vert s_n)\)采样\(K\)个动作。在实操中，我们发现\(q(\cdot \vert s_n) = \pi_{\theta_i}(\cdot \vert s_n)\)在连续问题中很好用，如机器人运动，而均匀分布在离散任务中很好用，比如Atari游戏，在这些任务中有时能取得更好的探索。

  对于每个状态\(s_n\)下采样到的动作\(a_{n,k}\)，我们通过操作一个从状态\(s_n\)和动作\(a_{n,k}\)开始的rollout（i.e. 一段短的轨迹）来估计\(\hat{Q}_{\theta_i}(s_n, a_n, k)\)。通过对每个K rollouts中的噪声使用相同的随机数序列（i.e. 普通随机数），可以极大地减小不同rollout之间Q值的方差。

  对于小且有限的动作空间，我们可以对每个给定的状态下可能的动作生成一个rollout。单个状态\(s_n\)对\(L_{\theta_{\text{old}}}\)的贡献为

\[L_n(\theta) = \sum_{k=1}^K \pi_\theta (a_k \mid s_n) \hat{Q}(s_n, a_k)\]

其中，状态空间为\(\mathcal{A} = \{ a_1, \ldots, a_K \}\)

  在大的或连续的状态空间中，我们可以利用重要性采样构造替代损失的估计器。单个状态\(s_n\)下得到的\(L_{\theta_{\text{old}}}\)自正则化估计量为

\[L_n(\theta) = \frac {\sum_{k=1}^K \frac{\pi_\theta\left(a_{n, k} \mid s_n\right)} {\pi_{\theta_{\text {old }}}\left(a_{n, k} \mid s_n\right)} \hat{Q}\left(s_n, a_{n, k}\right)} {\sum_{k=1}^K \frac{\pi_\theta\left(a_{n, k} \mid s_n\right)} {\pi_{\theta_{\text {old }}}\left(a_{n, k} \mid s_n\right)}}\]

假设我们从状态\(s_n\)开始执行\(K\)个动作\(a_{n,1}, a_{n,2}, \cdots, a_{n,K}\)。该自正则估计量去除了Q值（注意，在Q值中增加一个常数，梯度是不变的）使用基线的需要。对\(s_n \sim \rho(\pi)\)取平均，就得到了\(L_{\theta_{\text{old}}}\)的估计和它的梯度。

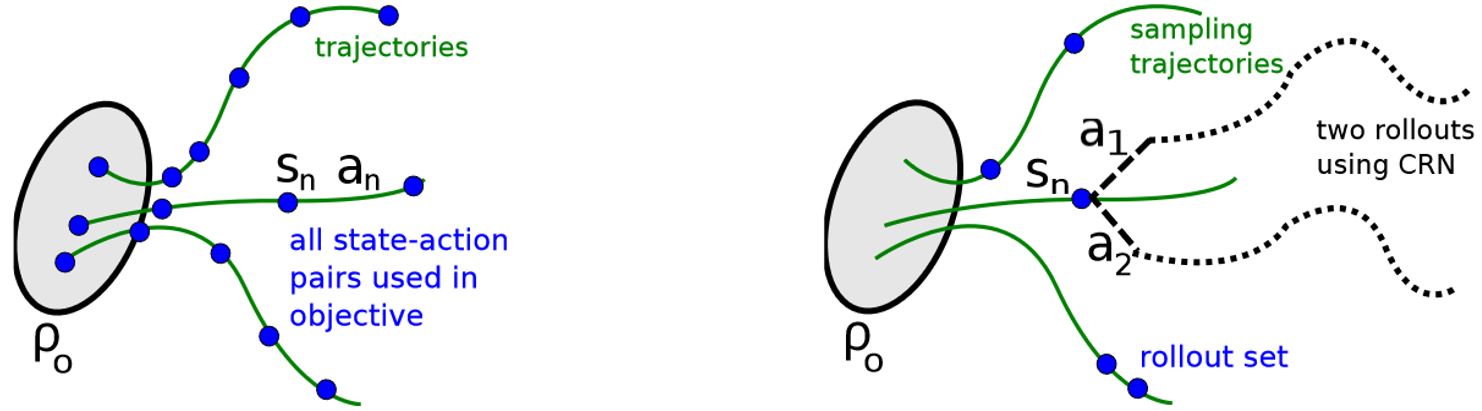
  Vine比single path好的地方在于，在代理损失中给定同样数量的Q值采样，vine对目标的本地估计具有更低的方差。即，vine对advantage值的估计更好。该方法的缺点在于必须对每个advantage做更多模拟。不仅如此，vine法需要对rollout集合中每个状态生成多条轨迹，这限制了算法可以将系统重置到任意状态的设定。与之相反，single path法无需状态重置且可直接在物理系统上实现。