贝叶斯学习

  发掘两个事件之间的联系（因果分析、前提和结论）
  反向思考

---

2.1 Bayes Theorem

\[\color{green}{ P(h \vert D) = \frac{P(D \vert h) P(h)}{P(D)} }\]

  \(\color{green}{P(h \vert D)}\)为事件\(h\)发生的后验概率
  \(\color{green}{P(h)}\)为事件\(h\)发生的先验概率
  \(\color{green}{P(D)}\)为事件\(D\)发生的先验概率
  \(\color{green}{P(D \vert h)}\)为已知事件\(h\)发生时事件\(D\)发生的概率

• 事件\(h\)发生的先验概率\(P(h)\)
    假设：互斥
    H space：完备
    \(\sum{P(h_i)=1}\)

• 事件\(D\)发生的先验概率\(P(D)\)
    把\(D\)作为所有可能数据的样本
    与\(h\)无关
    在不同假设的比较中可以被忽略

• 似然度（likelihood）\(P(D \vert h)\)
    对数似然度 \(\log(P(D \vert h))\)

2.2 选择假设

2.2.1 最大后验假设

一般来说，我们想要的是根据给定训练数据可能性最大的假设。

  最大后验假设（Maximum A Posteriori, MAP）\(h_{MAP}\)

\[\color{green}{\begin{aligned} h_{MAP} = & \mathop{argmax}_{h \in H} P(h \vert D) \\ = & \mathop{argmax}_{h \in H} \frac{P(D \vert h) P(h)}{P(D)} \\ = & \mathop{argmax}_{h \in H} P(D \vert h) P(h) \end{aligned}}\]

2.2.2 极大似然假设

  如果我们对假设一无所知，或者我们知道所有的假设都有相同的概率，那么MAP就是maximum likelihood（\(h_{ML}\)极大似然假设）。

\[\color{green}{ h_{MAP} = \mathop{argmax}_{h \in H} P(D \vert h) }\]

极大似然假设&最小均方误差

  训练数据：\(<x_i,d_i>\)

  \(d_i = f(x_i) + e_i\)
    \(d_i\)：独立样本
    \(f(x_i)\)：目标函数的无噪声值
    \(e_i\)：噪声，独立随机变量，正态分布\(N(0,\sigma^2)\)

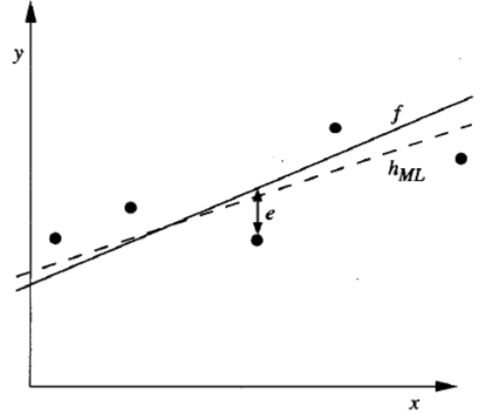
可得\(d_i\)：正态分布\(N(f(x_i),\sigma^2)\)

\[\begin{aligned} h_{ML} & = \mathop{argmax}_{h \in H} \sum_{i=1}^m \ln{\frac{1}{\sqrt{2 \Pi \sigma^2}}} - \frac{1}{2} (\frac{d_i - h(x_i)}{\sigma}) \\ & = \mathop{argmax}_{h \in H} \sum_{i=1}^m {-\frac{1}{2} (\frac{d_i - h(x_i)}{\sigma})} \\ & = \mathop{argmax}_{h \in H} \sum_{i=1}^m -(d_i - h(x_i))^2 \\ & = \mathop{argmin}_{h \in H} \sum_{i=1}^m (d_i - h(x_i))^2 \\ \end{aligned}\]

独立随机变量，正态分布噪声\(N(0,\sigma^2)\)，\(h_{ML} = h_{LSE}\)

2.2.3 朴素贝叶斯分类器

  假设目标函数\(f: X \rightarrow V\)，其中每个实例\(x = (a_1,a_2,\ldots,a_n)\)，那么\(f(x)\)最可能的值为\(v_{MAP} = \mathop{argmax}_{v_j \in V} P(x \vert v_j)P(v_j)\)。

Naive Bayes assumption:

\[P(x \vert v_j) = P(a_1,a_2,\ldots,a_n \vert v_j) = \prod_i P(a_i \vert v_j)\]

Naive Bayes classifier:

\[\begin{aligned} v_{NB} & = \mathop{argmax}_{v_j \in V} P(v_j) \prod_i P(a_i \vert v_j) \\ & = \mathop{argmax}_{v_j \in V} \{ \log P(v_j) + \sum_i \log P(a_i \vert v_j) \} \end{aligned}\]

如果满足独立属性条件，那么\(v_{MAP} = v_{NB}\)。

2.2.4 MDL (Minimum Description Length)

  Occam's razor: 倾向于最短的假设

  MDL：倾向于能够使\(h_{MDL} = \mathop{argmin}_{h \in H}\{ L_{C_1}(h) + L_{C_2}(D \vert h) \}\)最小的假设\(h\)
其中，\(L_C(x)\)是\(x\)在编码\(C\)下的描述长度。

MDL & MAP

\[\begin{aligned} h_{MAP} = & \mathop{argmax}_{h \in H} P(D \vert h) P(h) \\ = & \mathop{argmax}_{h \in H} \{ \log_2 P(D \vert h) + \log_2 P(h) \} \\ = & \mathop{argmin}_{h \in H} \{ - \log_2 P(D \vert h) - \log_2 P(h) \} \\ = & \mathop{argmin}_{h \in H} \{ L_{C_2}(D \vert h) - L_{C_1}(h) \} \\ = h_{MDL} \end{aligned}\]

权衡：假设的复杂性 vs. 假设所犯错误的数量
倾向于有一些错误的短假设而不是完美分类训练数据的长假设