Calculus of Variations and Optimal Control

2.1 Basic Concepts

2.1.1 Function and Functional

(1) Function

(2) Functional

  变量\(J\)是依赖于函数\(f(x)\)的泛函，记作\(J=J(f(x))\)，如果对每个函数\(f(x)\)，存在对应的\(J\)值。

2.1.2 Increment

(1) Increment of a Function

DEFINITION 2.1 函数\(f\)的增量，表示为\(\Delta f\)，定义为

\[\Delta f \triangleq f(t + \Delta t) - f(t) \tag{2.1.4}\]

从定义可以看出，\(\Delta f\)与自变量\(t\)和自变量的增量\(\Delta t\)都相关，严格来说，函数的增量需要写成形如\(\Delta f(t + \Delta t)\)的函数。

(2) Increment of a Functional

DEFINITION 2.2 泛函\(J\)的增量，表示为\(\Delta J\)，定义为

\[\begin{aligned} \boxed{\Delta J \triangleq J(x(t) + \delta x(t)) - J(x(t))} \end{aligned} \tag{2.1.7}\]

其中，\(\delta x(t)\)称为函数\(x(t)\)的variation。泛函的增量与函数\(x(t)\)及其增量\(\delta x(t)\)相关，严格来说，泛函的增量需要写成\(\Delta J(x(t) , \delta x(t))\)。

2.1.3 Differential and Variation

(1) Differential of a Function

  定义函数\(J\)在点\(t^*\)处的增量为

\[\Delta f \triangleq f(t^*+\Delta t) - f(t^*) \tag{2.1.10}\]

将\(f(t^*+\Delta t)\)在\(t^*\)处Taylor展开，得到

\[\Delta f = f(t^*) + \left( \frac{df}{dt} \right)_* \Delta t + \frac{1}{2!} \left( \frac{d^2f}{dt^2} \right)_* (\Delta t)^2 + \cdots - f(t^*) \tag{2.1.11}\]

忽略\(\Delta t\)中的高阶项，

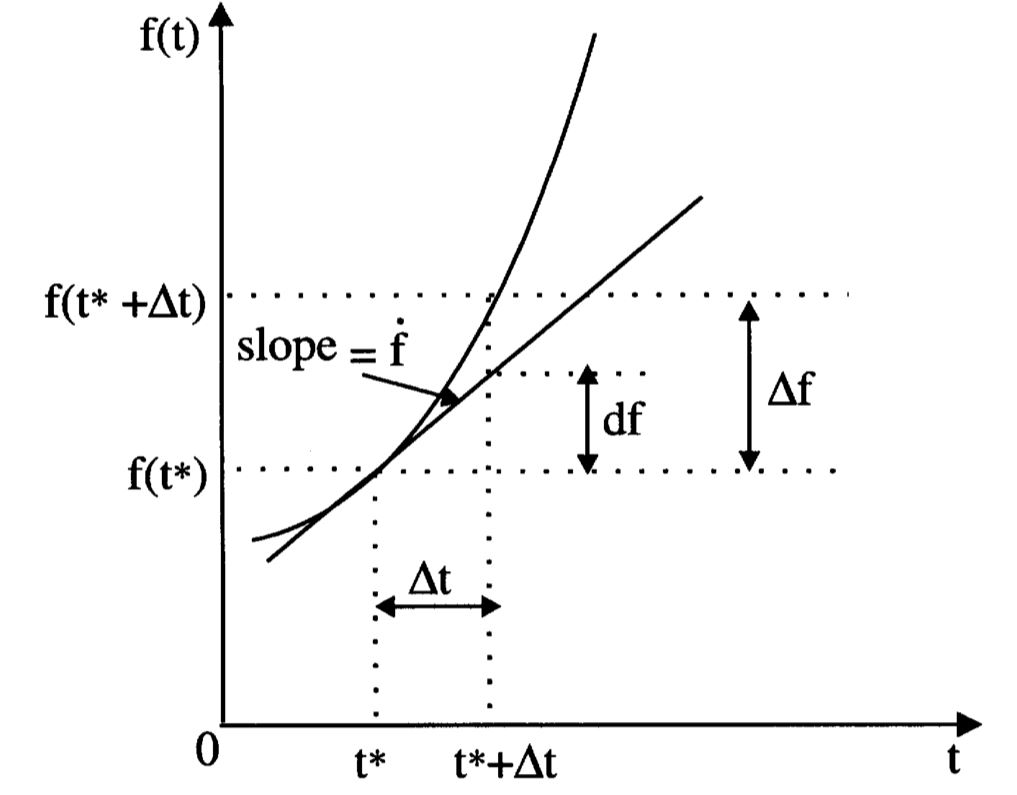
\[\Delta f = \left( \frac{df}{dt} \right)_* \Delta t = \dot{f}(t^*) \Delta t = df \tag{2.1.12}\]

其中，\(df\)称为\(f\)在点\(t^*\)处的differential。\(\dot{f}(t^*)\)是\(f\)在点\(t^*\)处的derivative或slope。换言之，微分\(df\)是增量\(\Delta t\)的一阶近似。增量、微分和导数的关系如图2.1所示。

(2) Variation of a Functional

  泛函的增量为

\[\Delta J \triangleq J(x(t)+\delta x(t)) - J(x(t)) \tag{2.1.14}\]

对\(J(x(t)+\delta x(t))\)进行Taylor展开，得到

\[\begin{aligned} \Delta J & = J(x(t)) + \frac{\partial J}{\partial x} \delta x(t) + \frac{1}{2!} \frac{\partial ^2 J}{\partial x^2} (\delta x(t))^2 + \cdots - J(x(t)) \\ & = \frac{\partial J}{\partial x} \delta x(t) + \frac{1}{2!} \frac{\partial ^2 J}{\partial x^2} (\delta x(t))^2 + \cdots \\ & = \delta J + \delta^2 J + \cdots \end{aligned} \tag{2.1.15}\]

其中，

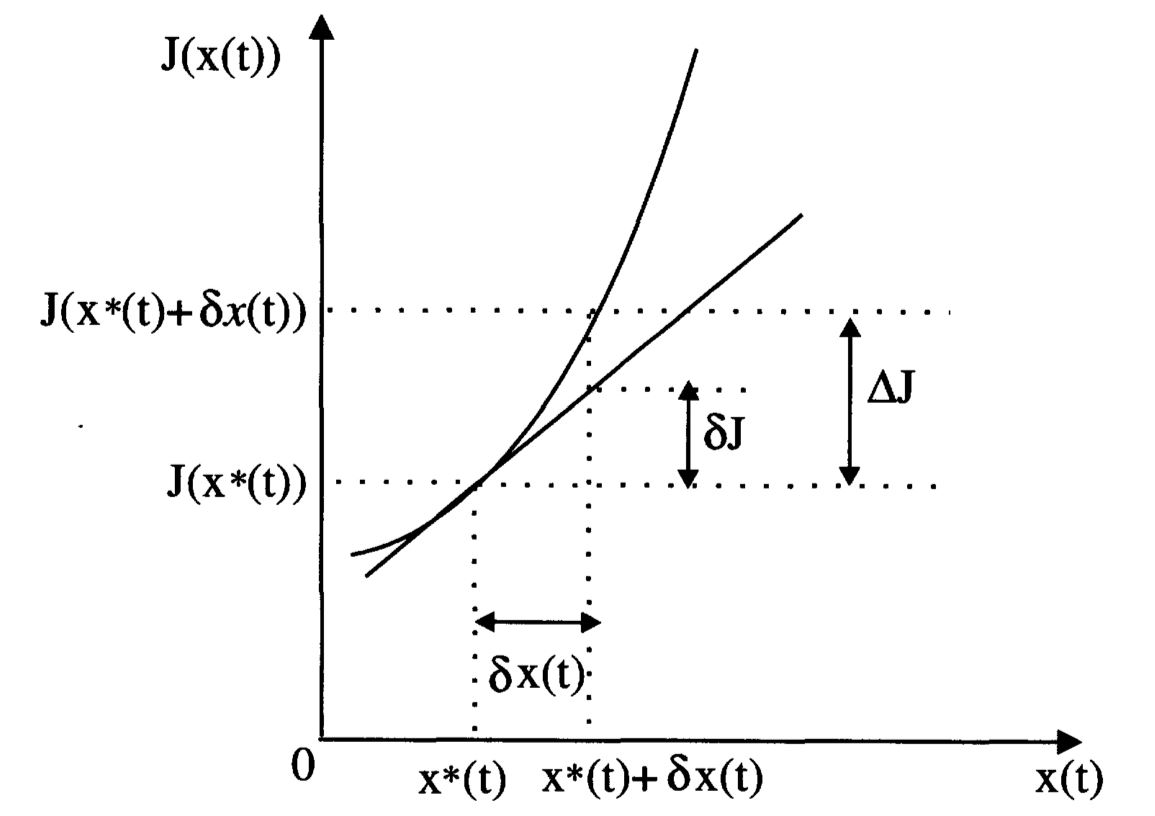
\[\delta J = \frac{\partial J}{\partial x} \delta x(t) \; \text{和} \; \delta^2 J = \frac{1}{2!} \frac{\partial ^2 J}{\partial x^2} (\delta x(t))^2 \tag{2.1.16}\]

分别称为泛函\(J\)的一阶变分和二阶变分。泛函\(J\)的一阶变分\(\delta J\)是增量\(\delta J\)的线性（一阶近似）部分。泛函的增量与一阶变分的关系如图2.2所示。

2.2 Optimum of a Function and a Functional

DEFINITION 2.3 Optimum of a Function：如果存在一个正数\(\epsilon\)，使得对于范围\(D\)内的所有点都有\(\vert t-t^* \vert \lt \epsilon\)，则称函数\(f(t)\)在点\(t^*\)处存在极值，\(f(t)\)的增量符号相同。

  函数取最值的必要条件为一阶微分消失，i.e.\(df=0\)。充分条件为：
  1.最小值：二阶微分为正，i.e.\(d^2 f \gt 0\)；
  2.最大值：二阶微分为负，i.e.\(d^2 f \lt 0\)。
如果\(d^2 f = 0\)，那么该点为驻点（或拐点）。

DEFINITION 2.4 Optimum of a Function：如果存在一个正的\(\epsilon\)，使得对于范围\(\Omega\)内的所有函数\(x\)都有\(\vert x-x^{*}\vert \lt \epsilon\)，则称泛函\(J\)在\(x^{*}\)处取到relative optimum，\(J\)的增量与之同符号。

  换言之，如果

\[\Delta J = J(x) - J(x^*) \ge 0 \tag{2.2.3}\]

那么\(J(x^*)\)为极小值。如果

\[\Delta J = J(x) - J(x^*) \le 0 \tag{2.2.4}\]

那么\(J(x^{*})\)为极大值。如果以上关系对于任意的\(\epsilon\)都成立，那么\(J(x^{*})\)为全局最值。

THEOREM 2.1 fundamental theorem of the calculus of variations
  \(x^{*}(t)\)为optimum的必要条件为：\(J\)在\(x^{*}(t)\)处的一阶变分为0，i.e.对于所有可能的\(\delta x(t)\)值，有\(\delta J(x^*(t),\delta x(t)) = 0\)。在此基础上，充分条件：对于最小值，有二阶变分\(\delta^2 J \gt 0\)；对于最大值，有二阶变分\(\delta^2 J \lt 0\)。

2.3 The Basic Variational Problem

2.3.1 Fixed-End Time and Fixed-End State System

  本节解决初始时间、状态和结束时间、状态都是确定的fixed-end time and fixed-end state问题。\(x(t)\)是一阶导数连续的标量函数，向量情况也可以类似处理。问题是要找到最优函数\(x^*(t)\)使得泛函

\[J(x(t)) = \int_{t_0}^{t_f} V(x(t),\dot{x}(t),t) \tag{2.3.1}\]

有相对最优。假设被积函数\(V\)一阶连续且对所有的参数二阶可偏微分，\(t_0\)和\(t_f\)确定，终点也确定，i.e.

\[x(t=t_0) ,\; x(t=t_f)=x_f \tag{2.3.2}\]

由定理2.1可知，最值的必要条件是泛函的变分消失。所以，要求\(x^*(t)\)，需要先定义增量，求变分，然后用定理2.1。

  fixed-end time and fixed-end state问题步骤如下：

• Step 1: Assumption of an Optimum
• Step 2: Variations and Increment
• Step 3: First Variation
• Step 4: Fundamental Theorem
• Step 5: Fundamental Lemma
• Step 6: Euler-Lagrange Equation

Step 1: Assumption of an Optimum

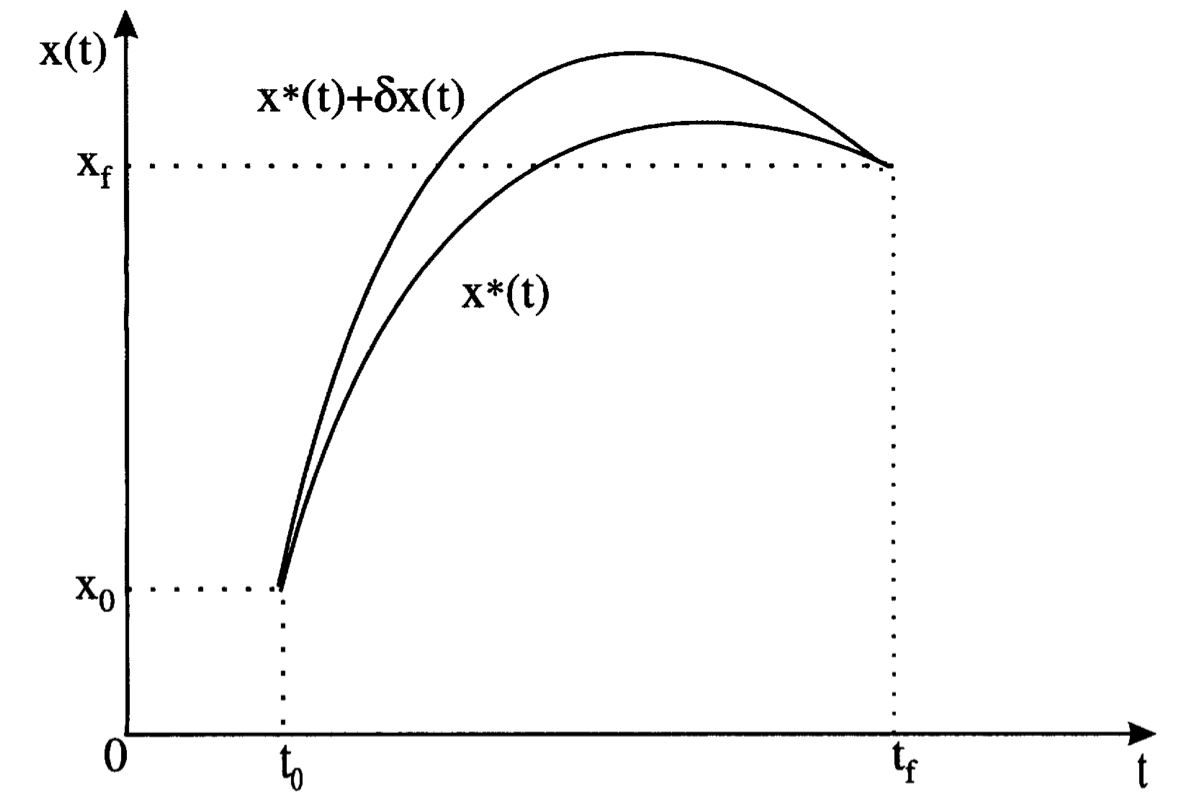
  假设\(x^*(t)\)为最优解，取\(x^*(t)\)附近的函数\(x_a(t)= x^*(t) + \delta x(t)\)，其中\(\delta x(t)\)是如图2.4所示的变分。函数\(x_a(t)\)满足边界条件(2.3.2)，因此必须满足

\[\delta x(t_0) = \delta x(t_f) = 0 \tag{2.3.3}\]

Step 2: Variations and Increment

  定义增量为

\[\begin{aligned} \Delta J(x^*(t),\delta x(t)) \triangleq & J(x^*(t) + \delta x(t) , \dot{x}^*(t) + \delta \dot{x}(t) ,t) \\ & - J(x^*(t),\dot{x}^*(t),t) \\ = & \int_{t_0}^{t_f} {V(x^*(t) + \delta x(t) , \dot{x}^*(t) + \delta \dot{x}(t) ,t) \, dt} \\ & - \int_{t_0}^{t_f} {V(x^*(t),\dot{x}^*(t),t) \, dt} \end{aligned} \tag{2.3.4}\]

将积分合并，得到

\[\begin{aligned} \Delta J(x^*(t),\delta x(t)) = & \int_{t_0}^{t_f} [ V(x^*(t) + \delta x(t) , \dot{x}^*(t) + \delta \dot{x}(t) ,t) \\ & - V(x^*(t),\dot{x}^*(t),t)] \, dt \end{aligned} \tag{2.3.5}\]

其中，

\[\dot{x}(t) = \frac{dx(t)}{dt} \quad \text{and} \quad \delta \dot{x}(t) = \frac{d}{dt}\{ \delta x(t) \} \tag{2.3.6}\]

对式(2.3.5)中的\(V\)关于点\(x^*(t)\)和\(\dot{x}^*(t)\)作Taylor展开

\[\begin{aligned} \Delta J = & \Delta J(x^*(t),\delta x(t)) \\ = & \int_{t_0}^{t_f} \bigg [ \frac{\partial V(x^*(t),\dot{x}^*(t),t)}{\partial x} \delta x(t) + \frac{\partial V(x^*(t),\dot{x}^*(t),t)}{\partial \dot{x}} \delta \dot{x}(t) \\ & + \frac{1}{2!} \left \{ \frac{\partial ^2 V(\cdots)}{\partial x^2}(\delta x(t))^2 + \frac{\partial ^2 V(\cdots)}{\partial \dot{x}^2}(\delta \dot{x}(t))^2 + 2 \frac{\partial ^2 V(\cdots)}{\partial x \partial \dot{x}} \right \} + \cdots \bigg] dt \end{aligned} \tag{2.3.7}\]

Step 3: First Variation

  保留\(\delta x(t)\)和\(\delta \dot{x}(t)\)中的线性项，得到变分

\[\delta J(x^*(t),\delta x(t)) = \int_{t_0}^{t_f} \bigg [ \frac{\partial V(x^*(t),\dot{x}^*(t),t)}{\partial x} \delta x(t) + \frac{\partial V(x^*(t),\dot{x}^*(t),t)}{\partial \dot{x}} \delta \dot{x}(t) \bigg] dt \tag{2.3.8}\]

为了完全用含\(\delta x(t)\)的项来表示，可以对第二项进行分部积分

\[\begin{aligned} \int_{t_0}^{t_f} \left( \frac{\partial V}{\partial \dot{x}} \right)_* \delta \dot{x}(t) dt & = \int_{t_0}^{t_f} \left( \frac{\partial V}{\partial \dot{x}} \right)_* \frac{d}{dt} (\delta x(t)) dt \\ & = \int_{t_0}^{t_f} \left( \frac{\partial V}{\partial \dot{x}} \right)_* d(\delta x(t)) \\ & = \left[ \left( \frac{\partial V}{\partial \dot{x}} \right)_* \delta x(t) \right] _{t_0}^{t_f} - \int_{t_0}^{t_f} \delta x(t) \frac{d}{dt} \left( \frac{\partial V}{\partial \dot{x}} \right)_* dt \end{aligned} \tag{2.3.9}\]

把式(2.3.9)代入(2.3.8)得到一阶变分为

\[\begin{aligned} \delta J(x^*(t),\delta x(t)) = & \int_{t_0}^{t_f} \left( \frac{\partial V}{\partial x} \right)_* \delta x(t) dt + \left[ \left( \frac{\partial V}{\partial \dot{x}} \right)_* \delta x(t) \right] _{t_0}^{t_f} \\ & - \int_{t_0}^{t_f} \delta x(t) \frac{d}{dt} \left( \frac{\partial V}{\partial \dot{x}} \right)_* dt \\ = & \int_{t_0}^{t_f} \left[ \left( \frac{\partial V}{\partial x} \right)_* - \frac{d}{dt} \left( \frac{\partial V}{\partial \dot{x}} \right)_* \right] \delta x(t)dt \\ & + \left. \left[ \left( \frac{\partial V}{\partial \dot{x}} \right)_* \delta x(t) \right] \right| _{t_0}^{t_f} \end{aligned} \tag{2.3.10}\]

把式(2.3.3)的边界条件代入(2.3.10)，得到

\[\delta J(x^*(t),\delta x(t)) = \int_{t_0}^{t_f} \left[ \left( \frac{\partial V}{\partial x} \right)_* - \frac{d}{dt} \left( \frac{\partial V}{\partial \dot{x}} \right)_* \right] \delta x(t)dt \tag{2.3.11}\]

Step 4: Fundamental Theorem

  根据定理2.1（fundamental theorem of the calculus of variations），\(x^*(t)\)要存在，则\(\delta J(x^*(t),\delta x(t)) = 0\)

\[\int_{t_0}^{t_f} \left[ \left( \frac{\partial V}{\partial x} \right)_* - \frac{d}{dt} \left( \frac{\partial V}{\partial \dot{x}} \right)_* \right] \delta x(t)dt = 0 \tag{2.3.12}\]

Step 5: Fundamental Lemma

  为了简化方程(2.3.12)的条件，利用fundamental lemma of the calculus of variations

LEMMA 2.1 对于任意连续函数\(g(t)\)

\[\int_{t_0}^{t_f} {g(t) \delta x(t) dt} = 0 \tag{2.3.13}\]

其中，函数\(\delta x(t)\)在区间\([t_0,t_f]\)之间连续，那么函数\(g(t)\)在区间\([t_0,t_f]\)之间必定处处为零。

Step 6: Euler-Lagrange Equation

  根据引理2.1，\(x^*(t)\)是式(2.3.1)中泛函\(J\)的最优解的一个必要条件为

\[\left( \frac{\partial V(x^*(t),\dot{x}^*(t),t)}{\partial x} \right)_* - \frac{d}{dt} \left( \frac{\partial V(x^*(t),\dot{x}^*(t),t)}{\partial \dot{x}} \right)_* = 0 \tag{2.3.14}\]

可以简化为

\[\color{green}{ \begin{aligned} \boxed{ \left( \frac{\partial V}{\partial x} \right)_* - \frac{d}{dt} \left( \frac{\partial V}{\partial \dot{x}} \right)_* = 0 } \end{aligned} } \tag{2.3.15}\]

对所有的\(t \in [t_0,t_f]\)均成立，此方程称为Euler equation。

2.3.2 Discussion on Euler-Lagrange Equation

  1.EL方程的变形

\[\begin{aligned} \boxed{ V_x - V_{t \dot{x}} - V_{x \dot{x}}\dot{x}^*(t) - V_{\dot{x} \dot{x}}\ddot{x}^*(t) = 0 } \end{aligned} \tag{2.3.19}\]

  2.EL方程(2.3.14)是微分方程。

  3.\(\frac{\partial V(x^*(t),\dot{x}^*(t),t)}{\partial \dot{x}}\)是关于\(x^*(t)\)、\(\dot{x}^*(t)\)和\(t\)的函数，所以该函数是可微的。从EL方程的变形的变形也可以看出，微分方程(2.3.14)一般是二阶的。

  4.如果有涉及\(\ddot{x}^*(t)\)、\(\dot{x}^*(t)\)和\(t\)的乘积或幂的项，那么这个微分方程会变成非线性的。

  5.系数可能是时变的。

  6.起点和终点处的条件会带来边值问题。

  7.Euler-Lagrange方程一般来说，是一个非线性、时变、两点边值、二阶常微分方程。因此，我们得到了一个非线性两点边值问题（TPBVP）。

  8.满足EL方程只是最优解的必要条件。

2.3.3 Different Cases for Euler-Lagrange Equation

Case 1：\(V\)与\(\dot{x}(t)\)和\(t\)相关，即\(V = V(\dot{x}(t),t)\)。那么\(V_x = 0\)。EL方程变为

\[\frac{d}{dt} (V_{\dot{x}}) = 0 \tag{2.3.20}\]

所以，有

\[V_{\dot{x}} = \frac{\partial V(\dot{x}^*(t),t)}{\partial \dot{x}} = C \tag{2.3.21}\]

其中，\(C\)为积分常数。

Case 2：\(V\)仅与\(\dot{x}(t)\)相关，即\(V = V(\dot{x}(t))\)。那么\(V_x = 0\)。EL方程变为

\[\frac{d}{dt} (V_{\dot{x}}) = 0 \rightarrow V_{\dot{x}} = C \tag{2.3.22}\]

一般来说，(2.3.21)或(2.3.22)的解

\[\dot{x}^*(t) = C_1 \rightarrow x^*(t) = C_1 t + C_2 \tag{2.3.23}\]

是直线方程。

Case 3：\(V\)与\(x(t)\)和\(\dot{x}(t)\)相关，即\(V = V(x(t),\dot{x}(t))\)。那么\(V_{t \dot{x}} = 0\)。(2.3.19)形式的EL方程变为

\[V_x -V{x \dot{x}} - V_{\dot{x} \dot{x}} \ddot{x}^*(t) = 0 \tag{2.3.24}\]

两边同时乘上\(\dot{x}^*(t)\)，得

\[\dot{x}^*(t) [V_x -V{x \dot{x}} - V_{\dot{x} \dot{x}} \ddot{x}^*(t)] = 0 \tag{2.3.25}\]

可以化成

\[\frac{d}{dt} (V - \dot{x}^*(t)V_{\dot{x}}) = 0 \rightarrow V - \dot{x}^*(t)V_{\dot{x}} = C \tag{2.3.26}\]

上述方程解法很多，比如变量分离法。

Case 4：\(V\)与\(x(t)\)和\(t\)相关，即\(V = V(x(t),t)\)。那么\(V_{\dot{x}} = 0\)。EL方程变为

\[\frac{\partial V(x^*(t),t)}{\partial x} = 0 \tag{2.3.27}\]

该方程的解不包含任意常数，因此一般来说不满足边界条件\(x(t_0)\)和\(x(t_f)\)。因此，一般来说，这种变分问题无解。只有少数函数\(x(t)\)满足边界条件的情况下，它才是最优解。

  变分法的一个经典例子就是最速降线（brachistochrone）问题，几乎所有关于变分法的书籍都涉及这个问题。

2.4 The Second Variation

  为了确定最优解，需要考虑二阶变分

\[\delta^2 J = \int_{t_0}^{t_f} \frac{1}{2!} \left[ \left( \frac{\partial^2 V}{\partial x^2} \right)_* (\delta x(t))^2 + \left( \frac{\partial^2 V}{\partial \dot{x}^2} \right)_* (\delta \dot{x}(t))^2 + 2 \left( \frac{\partial^2 V}{\partial x \partial \dot{x}} \right)_* \delta x(t) \delta \dot{x}(t) \right] dt \tag{2.4.1}\]

考虑上式的最后一项，采用分部积分法将其改写成只有\(\delta x(t)\)的形式。然后利用条件\(\delta x(t_0) = \delta x(t_f) = 0\)，可得

\[\delta^2 J = \frac{1}{2} \int_{t_0}^{t_f} \left[ \left \{ \left( \frac{\partial^2 V}{\partial x^2} \right)_* - \frac{d}{dt} \left( \frac{\partial^2 V}{\partial x \partial \dot{x}} \right)_* \right \} (\delta x(t))^2 + \left( \frac{\partial^2 V}{\partial \dot{x}^2} \right)_* (\delta \dot{x}(t))^2 \right] dt \tag{2.4.2}\]

根据定理2.1，充分条件还需要满足：要求最小值，\(\delta^2 J \lt 0\)。也就是说，对于任意的\(\delta x(t)\)和\(\delta \dot{x}(t)\)，满足

\[\left( \frac{\partial^2 V}{\partial x^2} \right)_* - \frac{d}{dt} \left( \frac{\partial^2 V}{\partial x \partial \dot{x}} \right)_* \gt 0 , \tag{2.4.3}\] \[\left( \frac{\partial^2 V}{\partial \dot{x}^2} \right)_* \gt 0 \tag{2.4.4}\]

对于最大值，以上条件的符号不变。取而代之的是，将二阶变分(2.4.1)改写成矩阵形式

\[\begin{aligned} \delta^2 J & = \frac{1}{2} \int_{t_0}^{t_f} { \begin{bmatrix} \delta x(t) & \delta \dot{x}(t) \\ \end{bmatrix} \begin{bmatrix} \frac{\partial^2 V}{\partial x^2} & \frac{\partial^2 V}{\partial x \partial \dot{x}} \\[2ex] \frac{\partial^2 V}{\partial x \partial \dot{x}} & \frac{\partial^2 V}{\partial \dot{x}^2} \\ \end{bmatrix} \begin{bmatrix} \delta x(t) \\ \delta \dot{x}(t) \\ \end{bmatrix} }dt \\ & = \frac{1}{2} \int_{t_0}^{t_f} { \begin{bmatrix} \delta x(t) & \delta \dot{x}(t) \end{bmatrix} \Pi \begin{bmatrix} \delta x(t) \\ \delta \dot{x}(t) \\ \end{bmatrix} }dt \end{aligned} \tag{2.4.5}\]

如果，矩阵\(\Pi\)是正（负）定的，就可以得到最小（大）值。大多数情况下，由于\(\delta x(t)\)是任意的，所以\((\delta \dot{x}(t))^2\)的系数，i.e.\(\partial^2 V / \partial \dot{x}^2\)决定了\(\delta^2 J\)的正负。也就是说，二阶变分的符号与\(\color{blue}{\partial^2 V / \partial \dot{x}^2}\)相同。因此，最小化要求

\[\color{green}{ \boxed{ \left( \frac{\partial^2 V}{\partial \dot{x}^2} \right)_* \gt 0 } } \tag{2.4.7}\]

对于最大化，上式的符号不变。该条件称为Legendre condition（或Legendre-Jacobi condition）。

2.5 Extrema of Functions with Conditions

  求解函数条件极值的两种方法：1.Direct Method；2.Lagrange multiplier method。

2.5.1 Direct Method

  求函数\(f(x_1,x_2)\)的极值，\(x_1,x_2\)是interdependent（相关）的变量，满足条件

\[g(x_1,x_2) = 0 \tag{2.5.16}\]

由极值的必要条件，有

\[df = \frac{\partial f}{\partial x_1} dx_1 + \frac{\partial f}{\partial x_2} dx_2 = 0 \tag{2.5.17}\]

然而由于条件(2.5.16)，所以\(dx_1\)和\(dx_2\)不是任意的，它们之间需要满足关系

\[dg = \frac{\partial g}{\partial x_1} dx_1 + \frac{\partial g}{\partial x_2} dx_2 = 0 \tag{2.5.18}\]

  为了同时满足条件(2.5.16)和极值条件(2.5.17)，假设\(x_1\)为自变量，\(x_2\)为因变量。假设\(\partial g / \partial x_2 \neq 0\)，那么(2.5.18)变为

\[dx_2 = - \left\{ \frac{\partial g / \partial x_1}{\partial g / \partial x_2} \right\} dx_1 \tag{2.5.20}\]

代入(2.5.17)得

\[df = \left[ \frac{\partial f}{\partial x_1} - \frac{\partial f}{\partial x_2} \left\{ \frac{\partial g / \partial x_1}{\partial g / \partial x_2} \right\} \right] dx_1 = 0 \tag{2.5.21}\]

假设\(dx_1\)是任意的，为了满足(2.5.21)，\(dx_1\)应该为0，即

\[\left( \frac{\partial f}{\partial x_1} \right) \left( \frac{\partial g}{\partial x_2} \right) - \left( \frac{\partial f}{\partial x_2} \right) \left( \frac{\partial g}{\partial x_1} \right) = 0 \tag{2.5.22}\]

上式和条件(2.5.16)可同时求出最优解\(x_1^*\)和\(x_2^*\)。方程(2.5.23)可以改写成行列式形式

\[\left| \begin{array}{cccc} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2} \\[2ex] \frac{\partial g}{\partial x_1} & \frac{\partial g}{\partial x_2} \end{array} \right| = 0 \tag{2.5.23}\]

  \(f\)和\(g\)的Jacobian（雅可比行列式）与\(x_1\)和\(x_2\)均相关，这种直接消去因变量的方法对于求解高阶问题很麻烦。

2.5.2 Lagrange Multiplier Method

  利用augmented Lagrangian function（增广拉格朗日函数）

\[\mathcal{L}(x_1,x_2,\lambda) = f(x_1,x_2) + \lambda g(x_1,x_2) \tag{2.5.25}\]

其中，\(\lambda\)是Lagrange multipier。把条件(2.5.16)代入Lagrangian，得

\[\mathcal{L}(x_1,x_2) = f(x_1,x_2) \tag{2.5.26}\]

因此，极值的一个必要条件为

\[df = d \mathcal{L} = 0 \tag{2.5.27}\]

或

\[d \mathcal{L} = df + \lambda dg = 0 \tag{2.5.28}\]

把(2.5.17)和(2.5.18)代入(2.5.28)可得

\[\left[ \frac{\partial f}{\partial x_1} + \lambda \frac{\partial g}{\partial x_1} \right] dx_1 + \left[ \frac{\partial f}{\partial x_2} + \lambda \frac{\partial g}{\partial x_2} \right] dx_2 = 0 \tag{2.5.29}\]

此时的\(dx_1\)和\(dx_2\)都是不独立的，因此无法直接得出两者系数都必须为0的结论。现假设\(dx_1\)是独立微分，那么根据(2.5.18)有\(dx_2\)是不独立微分。然后选择我们引入的乘数\(\lambda\)，让\(\lambda\)取使得\(dx_2\)系数为0的值\(\lambda ^*\)，即

\[\frac{\partial f}{\partial x_2} + \lambda^* \frac{\partial g}{\partial x_2} = 0 \tag{2.5.30}\]

这样，我们就可以把式(2.5.29)化简得到

\[\left[ \frac{\partial f}{\partial x_1} + \lambda \frac{\partial g}{\partial x_1} \right] dx_1 = 0 \tag{2.5.31}\]

由于\(dx_1\)是独立的微分，它的取值是任意的，所以上式只有当系数为0的时候成立，即

\[\frac{\partial f}{\partial x_1} + \lambda^* \frac{\partial g}{\partial x_1} = 0 \tag{2.5.32}\]

根据augmented Lagrangian function(2.5.25)，由

\[\frac{\partial \mathcal{L}}{\partial \lambda} = 0 \tag{2.5.33}\]

得出约束条件(2.5.16)。将(2.5.32)(2.5.30)和(2.5.33)的结果综合起来，可以得到

\[\frac{\partial \mathcal{L}}{\partial x_1} = \frac{\partial f}{\partial x_1} + \lambda^* \frac{\partial g}{\partial x_1} = 0 \tag{2.5.34}\] \[\frac{\partial \mathcal{L}}{\partial x_2} = \frac{\partial f}{\partial x_2} + \lambda^* \frac{\partial g}{\partial x_2} = 0 \tag{2.5.35}\] \[\frac{\partial \mathcal{L}}{\partial \lambda} = g(x_1^*,x_2^*) = 0 \tag{2.5.36}\]

以上三个式子可以同时求解出\(x_1^*\)，\(x_2^*\)和\(\lambda^*\)。消去(2.5.34)和(2.5.35)中的\(\lambda^*\)，可得

\[\left( \frac{\partial f}{\partial x_1} \right) \left( \frac{\partial g}{\partial x_2} \right) - \left( \frac{\partial f}{\partial x_2} \right) \left( \frac{\partial g}{\partial x_1} \right) = 0 \tag{2.5.37}\]

和直接法得到的(2.5.22)一样。

  总结：函数\(f(x_1,x_2)\)在条件\(g(x_1,x_2)=0\)下的极值等于增广函数\(\mathcal{L}(x_1,x_2,\lambda) = f(x_1,x_2)+\lambda g(x_1,x_2)\)的极值，尽管\(x_1\)，\(x_2\)和\(\lambda\)是互不相关的。

THEOREM 2.2 求连续的实值函数\(f(\mathbf{x}) = f(x_1,x_2,\cdots,x_n)\)的极值，函数满足条件

\[g_1(\mathbf{x}) = g_1(x_1,x_2,\cdots,x_n) = 0 \\ g_2(\mathbf{x}) = g_2(x_1,x_2,\cdots,x_n) = 0 \\ \vdots \\ g_m(\mathbf{x}) = g_m(x_1,x_2,\cdots,x_n) = 0 \tag{2.5.38}\]

其中，\(f\)和\(g\)有连续偏导数，且\(m \lt n\)。令\(\lambda_1,\lambda_2,\cdots,\lambda_m\)为与\(m\)个条件相对应的Lagrange multipliers，得到增广Lagrangian函数

\[\mathcal{L}(\mathbf{x,\lambda}) = f(\mathbf{x}) + \pmb{\lambda ^T g (x)} \tag{2.5.39}\]

其中，\(\pmb{\lambda ^T}\)是\(\pmb{\lambda}\)的转置。那么。最优值\(\mathbf{x}^*\)和\(\pmb{\lambda}^*\)是以下\(n+m\)个方程的解

\[\frac{\partial \mathcal{L}}{\partial \mathbf{x}} = \frac{\partial f}{\partial \mathbf{x}} + \pmb{\lambda ^T} \frac{\partial \mathbf{g}}{\partial \mathbf{x}} = 0 \tag{2.5.40}\] \[\frac{\partial \mathcal{L}}{\partial \pmb{\lambda}} = \mathbf{g(x)} = 0 \tag{2.5.41}\]

Features of Lagrange Multiplier：拉格朗日乘数法是求解函数条件极值的有效方法，有以下优势：

1. 将求解函数条件极值问题嵌入到求单个增广函数极值的过程中。
2. 可以在增广函数\(\mathcal{L}(\mathbf{x,\lambda})\)中同时处理所有相互独立的变量\(\mathbf{x}\)和\(\pmb{\lambda}\)。
3. 乘数\(\lambda\)在2的过程中起类似于催化剂的作用。
4. 拉格朗日乘数法的特点是增广维数\((n+m)\)，其相对简单和系统的计算过程通常可以补偿这点。

2.6 Extrema of Functionals with Conditions

  以只有两个变量的泛函为例，推导出必要条件，然后推广到n阶向量的情况。考虑以泛函形式表示的性能指标的极值

\[J(x_1(t),x_2(t),t) = J = \int_{t_0}^{t_f} { V(x_1(t),x_2(t),\dot{x}_1(t),\dot{x}_2(t),t) } dt \tag{2.6.1}\]

满足条件（设备或系统方程）

\[g(x_1(t),x_2(t),\dot{x}_1(t),\dot{x}_2(t)) = 0 \tag{2.6.2}\]

以及fixed-end-point条件

\[x_1(t_0) = x_{10} , \quad x_2(t_0) = x_{20} ; \quad x_1(t_f) = x_{1f} , \quad x_2(t_f) = x_{2f} \tag{2.6.3}\]

解决这个问题有以下几个步骤：

• Step 1: Lagrangian
• Step 2: Variations and Increment
• Step 3: First Variation
• Step 4: Fundamental Theorem
• Step 5: Fundamental Lemma
• Step 6: Euler-Lagrange Equation

Step 1: Lagrangian

  构造增广泛函

\[J_a = \int_{t_0}^{t_f} { \mathcal{L}(x_1(t),x_2(t),\dot{x}_1(t),\dot{x}_2(t),\lambda (t),t) } dt \tag{2.6.4}\]

其中，\(\lambda (t)\)是拉格朗日乘数，拉格朗日函数\(\mathcal{L}\)的定义为

\[\begin{aligned} \mathcal{L} = & \mathcal{L}(x_1(t),x_2(t),\dot{x}_1(t),\dot{x}_2(t),\lambda (t),t) \\ = & V(x_1(t),x_2(t),\dot{x}_1(t),\dot{x}_2(t),t) + \lambda(t) g(x_1(t),x_2(t),\dot{x}_1(t),\dot{x}_2(t)) \end{aligned} \tag{2.6.5}\]

从性能指标(2.6.1)和增广性能指标(2.6.4)中可以看出，对于任意\(\lambda (t)\)，如果条件(2.6.2)满足，则有\(J_a = J\)。

Step 2: Variations and Increment

  假设最优值，然后写出变分和增量

\[x_i(t) = x_i^*(t) + \delta x_i(t) , \quad \dot{x}_i(t) = \dot{x}_i^*(t) + \delta \dot{x}_i(t) , \qquad i = 1,2 \\ \Delta J_a = J_a(x_i^*(t) + \delta x_i(t),\dot{x}_i^*(t) + \delta \dot{x}_i(t),t) - J_a(x_i^*(t),\dot{x}_i^*(t),t) , \text{for } i = 1,2 \tag{2.6.6}\]

Step 3: First Variation

对\(J_a\)的一阶变分作Taylor展开，然后保留线性项，得到

\[\begin{aligned} \delta J_a = \int_{t_0}^{t_f} \bigg[ & \left( \frac{\partial \mathcal{L}}{\partial x_1} \right)_* \delta x_1(t) + \left( \frac{\partial \mathcal{L}}{\partial x_2} \right)_* \delta x_2(t) \\ + & \left( \frac{\partial \mathcal{L}}{\partial \dot{x}_1} \right)_* \delta \dot{x}_1(t) + \left( \frac{\partial \mathcal{L}}{\partial \dot{x}_2} \right)_* \delta \dot{x}_2(t) \bigg] dt \end{aligned} \tag{2.6.7}\]

和之前CoV的部分一样，将含\(\delta \dot{x}_1(t)\)和\(\delta \dot{x}_2(t)\)的项改写为只含\(\delta x_1(t)\)和\(\delta x_2(t)\)的形式（利用分部积分法）

\[\int_{t_0}^{t_f} { \left(\frac{\partial \mathcal{L}}{\partial x_1} \right)_* \delta \dot{x}_1(t) } dt = \left. \left[ \left(\frac{\partial \mathcal{L}}{\partial \dot{x}_1}\right)_* \delta x_1(t) \right] \right| _{t_0}^{t_f} - \int_{t_0}^{t_f} { \frac{d}{dt} \left(\frac{\partial \mathcal{L}}{\partial \dot{x}_1}\right)_* \delta x_1(t) } dt \tag{2.6.8}\]

然后，一阶变分可以化成

\[\begin{aligned} \delta J_a = & \int_{t_0}^{t_f} \bigg[ \left( \frac{\partial \mathcal{L}}{\partial x_1} \right)_* \delta x_1(t) + \left( \frac{\partial \mathcal{L}}{\partial x_2} \right)_* \delta x_2(t) \bigg] dt \\ & + \left. \left[ \left(\frac{\partial \mathcal{L}}{\partial \dot{x}_1}\right)_* \delta x_1(t) \right] \right| _{t_0}^{t_f} + \left. \left[ \left(\frac{\partial \mathcal{L}}{\partial \dot{x}_2}\right)_* \delta x_2(t) \right] \right| _{t_0}^{t_f} \\ & - \int_{t_0}^{t_f} { \frac{d}{dt} \left(\frac{\partial \mathcal{L}}{\partial \dot{x}_1}\right)_* \delta x_1(t) } dt - \int_{t_0}^{t_f} { \frac{d}{dt} \left(\frac{\partial \mathcal{L}}{\partial \dot{x}_2}\right)_* \delta x_2(t) } dt \end{aligned} \tag{2.6.9}\]

由于要满足(2.6.3)的给定边界时间和状态，所以边界处应该是没有变分的。也就是说

\[\delta x_1 (t_0) = \delta x_2 (t_0) = \delta x_1 (t_f) = \delta x_1 (t_f) = 0 \tag{2.6.10}\]

把边界变分代入增广的一阶变分(2.6.9)中，得

\[\begin{aligned} \delta J_a = & \int_{t_0}^{t_f} \bigg[ \left( \frac{\partial \mathcal{L}}{\partial x_1} \right)_* - \frac{d}{dt} \left(\frac{\partial \mathcal{L}}{\partial \dot{x}_1}\right)_* \bigg] \delta x_1(t) dt \\ & + \int_{t_0}^{t_f} \bigg[ \left( \frac{\partial \mathcal{L}}{\partial x_2} \right)_* - \frac{d}{dt} \left(\frac{\partial \mathcal{L}}{\partial \dot{x}_2}\right)_* \bigg] \delta x_2(t) dt \\ \end{aligned} \tag{2.6.11}\]

Step 4: Fundamental Theorem

  1.利用变分法的基本原理（Theorem 2.1），让一阶变分为0。

  2.\(x_1(t)\)和\(x_2(t)\)根据条件(2.6.2)相关的，所以\(\delta x_1(t)\)和\(\delta x_2(t)\)都是不独立的。因此，我们选定\(\delta x_2(t)\)为自变分，\(\delta x_1(t)\)为因变分。

  3.决定乘数\(\lambda ^* (t)\)的值，令一阶变分的系数为0，即

\[\left( \frac{\partial \mathcal{L}}{\partial x_1} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{x}_1} \right)_* = 0 \tag{2.6.12}\]

这样，一阶变分(2.6.11)变为

\[\int_{t_0}^{t_f} { \bigg[ \left( \frac{\partial \mathcal{L}}{\partial x_2} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{x}_2} \right)_* \bigg] \delta x_2(t) } dt = 0 \tag{2.6.13}\]

Step 5: Fundamental Lemma

  利用CoV的基本引理（Lemma 2.1），由于\(\delta x_2(t)\)被选为独立变分，所以取值是任意的，要令(2.6.13)成立，就必须要让\(\delta x_1(t)\)的系数也消失，即

\[\left( \frac{\partial \mathcal{L}}{\partial x_2} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{x}_2} \right)_* = 0 \tag{2.6.14}\]

与此同时，从Lagrangian (2.6.5)要注意到

\[\left( \frac{\partial \mathcal{L}}{\partial \lambda} \right)_* = 0 \tag{2.6.15}\]

可以得到约束条件(2.6.2)。

Step 6: Euler-Lagrange Equation

  结合条件(2.6.12)(2.6.14)和(2.6.15)，泛函(2.6.1)在条件(2.6.2)下的极值需满足必要条件

\[\left( \frac{\partial \mathcal{L}}{\partial x_1} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{x}_1} \right)_* = 0 \tag{2.6.16}\] \[\left( \frac{\partial \mathcal{L}}{\partial x_2} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{x}_2} \right)_* = 0 \tag{2.6.17}\] \[\left( \frac{\partial \mathcal{L}}{\partial \lambda} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\lambda}} \right)_* = 0 \tag{2.6.18}\]

  对于n阶系统，考虑如下泛函的极值

\[J = \int_{t_0}{t_f} { V(\mathbf{x}(t),\mathbf{\dot{x}}(t),t)} dt \tag{2.6.19}\]

其中，\(\mathbf{x}\)为n阶状态向量，满足系统方程（条件）

\[g_i(\mathbf{x}(t),\mathbf{\dot{x}}(t),t) = 0 \qquad i=0,1,\ldots,m \tag{2.6.20}\]

以及边界条件\(\mathbf{x}(0)\)和\(\mathbf{x}(t_f)\)。构造增广泛函

\[J_a = \int_{t_0}^{t_f} { \mathcal{L} (\mathbf{x}(t),\mathbf{\dot{x}}(t),\pmb{\lambda}(t),t) } dt \tag{2.6.21}\]

其中，Lagrangian \(\mathcal{L}\)为

\[\color{green}{ \boxed{ \mathcal{L} (\mathbf{x}(t),\mathbf{\dot{x}}(t),\pmb{\lambda}(t),t) = V(\mathbf{x}(t),\mathbf{\dot{x}}(t),t) + \pmb{\lambda}^T(t) g_i(\mathbf{x}(t),\mathbf{\dot{x}}(t),t) } } \tag{2.6.22}\]

其中，Lagrange multiplier \(\lambda(t) = [\lambda_1(t),\lambda_2(t),\ldots,\lambda_m(t)]^T\)。对\(J_a\)用Euler-Lagrange方程得到

\[\color{green}{ \boxed{ \left( \frac{\partial \mathcal{L}}{\partial \mathbf{x}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}} \right)_* = 0 } } \tag{2.6.23}\] \[\color{green}{ \boxed{ \left( \frac{\partial \mathcal{L}}{\partial \pmb{\lambda}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{\lambda}}} \right)_* = 0 \rightarrow g_i(\mathbf{x}(t),\mathbf{\dot{x}}(t),t) = 0 } } \tag{2.6.24}\]

由(2.6.22)可知，Lagrange multiplier \(\lambda\)与\(\mathbf{\dot{\lambda}}(t)\)无关，因此Euler-Lagrange方程只是给出了被控对象或系统的条件。所以，我们可以根据给定的边界条件来求解EL方程。

2.7 Variational Approach to Optimal Control Systems

  利用变分法接近最优控制系统，引入Hamiltonian函数，Pontryagin和他的同事利用这个函数来发展了著名的Minimum Principle。

2.7.1 Terminal Cost Problem

  Bolza问题：性能指标的一般形式除了包含整体成本函数外，还包含最终(终端)成本函数。Bolza问题的性能指标形式最具一般性。

  考虑被控对象

\[\mathbf{\dot{x}}(t) = \mathbf{f} ( \mathbf{x}(t),\mathbf{u}(t),t ) \tag{2.7.1}\]

性能指标为

\[J(\mathbf{u}(t)) = S(\mathbf{x}(t_f),t_f) + \int_{t_0}^{t_f} {V(\mathbf{x}(t),\mathbf{u}(t),t)}dt \tag{2.7.2}\]

给定边界条件为

\[\mathbf{x}(t_0) = \mathbf{x}_0; \qquad \mathbf{x}(t_f) \text{ is free and } t_f \text{ is free} \tag{2.7.3}\]

其中，\(\mathbf{x}(t)\)和\(\mathbf{u}(t)\)分别为n维状态向量和r维控制向量。已知

\[\int_{t_0}^{t_f} { \frac{d S(\mathbf{x}(t),t)}{dt} } dt = S(\mathbf{x}(t),t)|_{t_0}^{t_f} = S(\mathbf{x}(t_f),t_f) - S(\mathbf{x}(t_0),t_0) \tag{2.7.4}\]

把式(2.7.4)代入初始的性能指标(2.7.2)中，得到

\[\begin{aligned} J_2(\mathbf{u}(t)) & = \int_{t_0}^{t_f} { \left[ V(\mathbf{x}(t),\mathbf{u}(t),t) + \frac{dS}{dt} \right] } dt \\ & = \int_{t_0}^{t_f} {V(\mathbf{x}(t),\mathbf{u}(t),t)} dt + S(\mathbf{x}(t_f),t_f) - S(\mathbf{x}(t_0),t_0) \end{aligned} \tag{2.7.5}\]

由于\(S(\mathbf{x}(t_0),t_0)\)的值是固定的，所以优化\(J\)和\(J_2\)本质上是一样的，因为这里只关注找到最优控制，而不关注最优成本。还有一点需要指出的是

\[\frac{d[S(\mathbf{x}(t),t)]}{dt} = \left( \frac{\partial S}{\partial \mathbf{x}} \right)^T \mathbf{\dot{x}}(t) + \frac{\partial S}{\partial t} \tag{2.7.6}\]

• Step 1: Assumption of Optimal Conditions
• Step 2: Variations of Control and State Vectors
• Step 3: Lagrange Multiplier
• Step 4: Lagrangian
• Step 5: First Variation
• Step 6: Condition for Extrema
• Step 7: Hamiltonian

Step 1: Assumption of Optimal Conditions

  假设\(\mathbf{x}^*(t)\)和\(\mathbf{u}^*(t)\)分别为状态和控制的最优值，那么

\[J(\mathbf{u}^*(t)) = \int_{t_0}^{t_f} { \left[ V(\mathbf{x}^*(t),\mathbf{u}^*(t),t) + \frac{dS(\mathbf{x}^*(t),t)}{dt} \right] } dt \\[2ex] \mathbf{\dot{x}}^*(t) = \mathbf{f}( ) \tag{2.7.7}\]

Step 2: Variations of Control and State Vectors

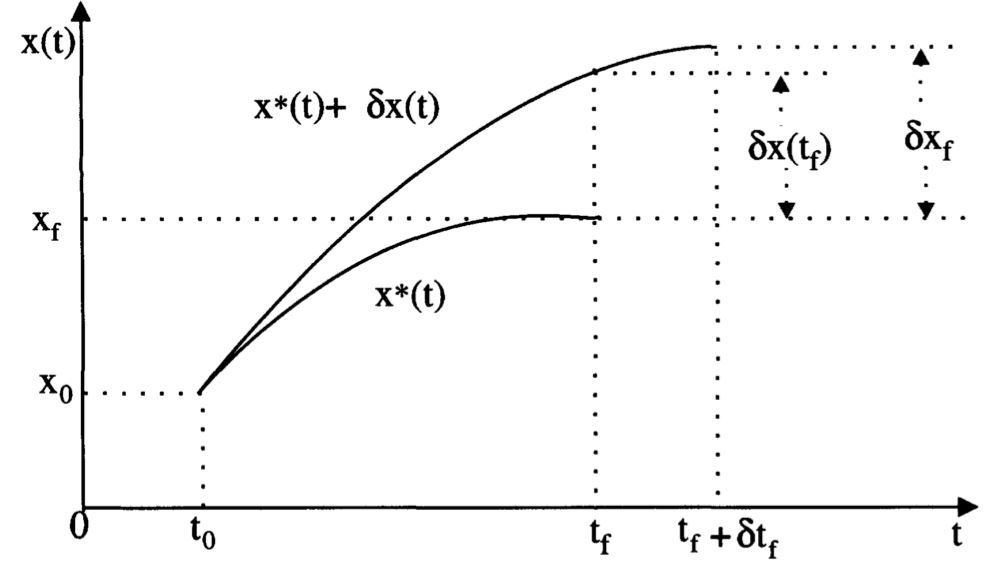
  考虑如图2.7所示的状态和控制向量的变分（扰动）

\[\mathbf{x}(t) = \mathbf{x}^*(t) + \delta \mathbf{x}(t) ,\quad \mathbf{u}(t) = \mathbf{u}^*(t) + \delta \mathbf{u}(t) \tag{2.7.8}\]

那么，状态方程(2.7.1)和性能指标(2.7.5)变为

\[\begin{aligned} & \mathbf{\dot{x}}^*(t) + \delta \mathbf{\dot{x}}(t) = \mathbf{f}(\mathbf{x}^*(t)+\delta \mathbf{x}(t), \mathbf{u}^*(t)+\delta \mathbf{u}(t), t ) \\ & J(\mathbf{u}^*(t)) = \int_{t_0}^{t_f + \delta t_f} { \left[ V(\mathbf{x}^*(t)+\delta \mathbf{x}(t), \mathbf{u}^*(t)+\delta \mathbf{u}(t), t ) + \frac{dS}{dt} \right] } dt \end{aligned} \tag{2.7.9}\]

Step 3: Lagrange Multiplier

   通过引入拉格朗日乘数向量\(\pmb{\lambda}(t)\)（也称协状态向量）和利用式(2.7.6)，可以得到性能指标在最优条件下为

\[\begin{aligned} J_a(\mathbf{u}^*(t)) = \int_{t_0}^{t_f} \big \{ [&V(\mathbf{x}^*(t),\mathbf{u}^*(t),t) + \left( \frac{\partial S}{\partial \mathbf{x}} \right)^T_* \mathbf{\dot{x}}^*(t) + \left( \frac{\partial S}{\partial t} \right)_* \\ + & \pmb{\lambda}^T(t) [\mathbf{f}(\mathbf{x}^*(t),\mathbf{u}^*(t),t) - \mathbf{\dot{x}}^*(t)] \big \} dt \end{aligned} \tag{2.7.10}\]

Step 4: Lagrangian

  定义最优条件下的Lagrangian函数

\[\begin{aligned} \mathcal{L} = & \mathcal{L} (\mathbf{x}^*(t),\mathbf{\dot{x}}^*(t),\mathbf{u}^*(t),\pmb{\lambda}(t),t) \\ = & V(\mathbf{x}^*(t),\mathbf{u}^*(t),t) + \left( \frac{\partial S}{\partial \mathbf{x}} \right)^T_* \mathbf{\dot{x}}^*(t) + \frac{\partial S}{\partial t} + \pmb{\lambda}^T(t) \{ \mathbf{f}(\mathbf{x}^*(t),\mathbf{u}^*(t),t) - \mathbf{\dot{x}}^*(t) \} \end{aligned} \tag{2.7.12}\]

增广的性能指标在最优条件下为

\[J_a(\mathbf{u}^*(t)) = \int_{t_0}^{t_f} { \mathcal{L} (\mathbf{x}^*(t),\mathbf{\dot{x}}^*(t),\mathbf{u}^*(t),\pmb{\lambda}(t),t) } dt = \int_{t_0}^{t_f} {\mathcal{L}} dt \tag{2.7.14}\]

利用均值定理和Taylor展开，只保留线性项，得到

\[\begin{aligned} \int_{t_f}^{t_f + \delta t_f} \mathcal{L}^{\delta} dt = & \mathcal{L}^{\delta} |_{t_f} \delta t_f \\ \approx & \left. \left \{ \mathcal{L} + \left( \frac{\partial \mathcal{L}}{\partial \mathbf{x}} \right)^T_* \delta \mathbf{x}(t) + \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}} \right)^T_* \delta \mathbf{\dot{x}}(t) + \left( \frac{\partial \mathcal{L}}{\partial \mathbf{u}} \right)^T_* \delta \mathbf{u}(t) \right\} \right |_{t_f} \delta t_f \\ \approx & \mathcal{L} |_{t_f} \delta t_f \end{aligned} \tag{2.7.15}\]

Step 5: First Variation

  定义增量\(\Delta J\)，利用Taylor展开，提取出一阶变分\(\delta J\)

\[\begin{aligned} & \Delta J = J_a(\mathbf{u}(t)) - J_a(\mathbf{u}^*(t)) = \int_{t_0}^{t_f} (\mathcal{L}^{\delta}- \mathcal{L})dt + \mathcal{L} |_{t_f} \delta t_f \\ & \delta J = \int_{t_0}^{t_f} \left\{ \left( \frac{\partial \mathcal{L}}{\partial \mathbf{x}} \right)^T_* \delta \mathbf{x}(t) + \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}} \right)^T_* \delta \mathbf{\dot{x}}(t) + \left( \frac{\partial \mathcal{L}}{\partial \mathbf{u}} \right)^T_* \delta \mathbf{u}(t) \right\} dt + \mathcal{L}|_{t_f} \delta t_f \end{aligned} \tag{2.7.16}\]

用分部积分法处理一阶变分中的含\(\delta \mathbf{\dot{x}}(t)\)项，结合条件\(\delta \mathbf{x}(t_0)\)（因为\(\mathbf{x}(t_0)\)是定值），得到处理后的一阶变分

\[\begin{aligned} \delta J = \int_{t_0}^{t_f} { \left[ \left( \frac{\partial \mathcal{L}}{\partial \mathbf{x}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}} \right)_* \right]^T \delta \mathbf{x}(t) } dt + \int_{t_0}^{t_f} { \left( \frac{\partial \mathcal{L}}{\partial \mathbf{u}} \right)^T_* \delta \mathbf{u}(t) } dt + \mathcal{L}|_{t_f} \delta t_f + \left. \left[ \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}} \right)^T_* \delta \mathbf{x}(t) \right] \right|_{t_f} \end{aligned} \tag{2.7.18}\]

Step 6: Condition for Extrema

  根据CoV的基本定理，一阶变分要为零。在典型控制系统中，如(2.7.1)，\(\delta \mathbf{u}(t)\)是独立的控制变分，而\(\delta \mathbf{x}(t)\)是不独立的状态变分。首先，令因变分\(\delta \mathbf{x}(t)\)的系数为零，得到Euler-Lagrange方程

\[\left( \frac{\partial \mathcal{L}}{\partial \mathbf{x}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}} \right)_* = 0 \tag{2.7.19}\]

然后，因为独立控制变分\(\delta \mathbf{u}(t)\)的值是任意的，所以它的系数应该为零，即

\[\left( \frac{\partial \mathcal{L}}{\partial \mathbf{u}} \right)_* = 0 \tag{2.7.20}\]

最后，一阶变分简化为

\[\mathcal{L}^* |_{t_f} \delta t_f + \left. \left[ \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}} \right)^T_* \delta \mathbf{x}(t) \right] \right|_{t_f} = 0 \tag{2.7.21}\]

注意，条件（或被控对象）方程(2.7.1)可以用Lagrangian (2.7.12)表示

\[\left( \frac{ \partial \mathcal{L} }{ \partial \pmb{\lambda} } \right)_* = 0 \tag{2.7.22}\]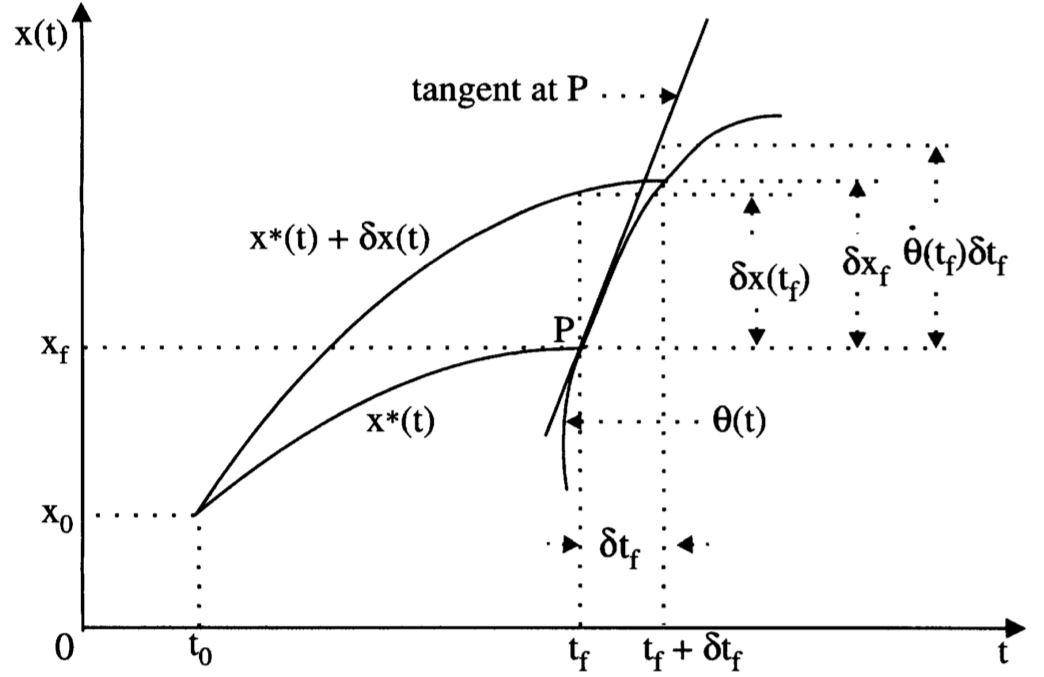

为了将含\(\delta \mathbf{x}(t)\)的(2.7.21)化成含有\(\delta \mathbf{x}_f\)（如图2.8），作近似化处理，得到

\[\mathbf{\dot{x}}^*(t_f) + \delta \mathbf{\dot{x}}(t_f) \approx \frac{\delta \mathbf{x}_f - \delta \mathbf{x}(t_f)}{\delta t_f} \tag{2.7.23}\]

保留\(\delta\)中的线性项，得到

\[\delta \mathbf{x}(t_f) = \delta \mathbf{x}_f - \mathbf{\dot{x}}^*(t_f) \delta t_f \tag{2.7.25}\]

把式(2.7.25)代入边界条件(2.7.21)，得到Lagrangian的一般边界条件

\[\left.\left[ \mathcal{L}^* - \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}(t)} \right)^T_* \mathbf{\dot{x}}(t) \right]\right|_{t_f} \delta t_f + \left. \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}(t)} \right)^T_* \right|_{t_f} \delta \mathbf{x}_f = 0 \tag{2.7.26}\]

Step 7: Hamiltonian

  定义最优情况下的Hamiltonian函数为

\[\color{green}{\boxed{ \mathcal{H}^* = V(\mathbf{x}^*(t), \mathbf{u}^*(t), t) + \pmb{\lambda}^{*T}(t) \mathbf{f}(\mathbf{x}^*(t), \mathbf{u}^*(t), t) } } \tag{2.7.27}\]

把\(\mathcal{H}^*\)代入\(\mathcal{L}^*\)得

\[\begin{aligned} \mathcal{L}^* = & \mathcal{L}^* (\mathbf{x}^*(t), \mathbf{\dot{x}}^*(t), \mathbf{u}^*(t), \pmb{\lambda}^*(t), t) \\ = & \mathcal{H}^*(\mathbf{x}^*(t), \mathbf{u}^*(t), \pmb{\lambda}^*(t), t) + \left( \frac{\partial S}{\partial \mathbf{x}} \right)_*^T \mathbf{\dot{x}}^*(t) + \left( \frac{\partial S}{\partial t} \right)_* - \pmb{\lambda}^{*T}(t) \mathbf{\dot{x}}^*(t) \end{aligned} \tag{2.7.28}\]

把式(2.7.28)代入(2.7.20)(2.7.19)和(2.7.22)，同时注意终点代价函数\(S = S(\mathbf{x}(t),t)\)，可以得到状态、控制以及协态方程，分别用Hamiltonian表示。因此，对于optimal control \(\color{green}{\mathbf{u}^*(t)}\)，式(2.7.20)变为

\[\left( \frac{\partial \mathcal{L}}{\partial \mathbf{u}} \right)_* = 0 \rightarrow \color{green}{\boxed{ \left( \frac{\partial \mathcal{H}}{\partial \mathbf{u}} \right)_* = 0 } } \tag{2.7.29}\]

对于optimal state \(\color{green}{\mathbf{x}^*(t)}\)，式(2.7.19)变为

\[\left( \frac{\partial \mathcal{L}}{\partial \mathbf{x}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \mathbf{\dot{x}}} \right)_* = 0 \rightarrow \color{green}{\boxed{ \left( \frac{\partial \mathcal{H}}{\partial \mathbf{x}} \right)_* = - \pmb{\dot{\lambda}}^*(t) } } \tag{2.7.30}\]

对于costate \(\color{green}{\pmb{\lambda}^*(t)}\)

\[\left( \frac{\partial \mathcal{L}}{\partial \pmb{\lambda}} \right)_* = 0 \rightarrow \color{green}{\boxed{ \left( \frac{\partial \mathcal{H}}{\partial \pmb{\lambda}} \right)_* = - \mathbf{\dot{x}}^*(t) } } \tag{2.7.31}\]

最后，利用式(2.7.28)，最优状态下的边界条件(2.7.26)简化为

\[\color{green}{\boxed{ \left[ \mathcal{H}^* + \frac{\partial S}{\partial t} \right]_{t_f} \delta t_f + \left[ \left( \frac{\partial S}{\partial \mathbf{x}} \right)_* - \pmb{\lambda}^*(t) \right]'_{t_f} \delta \mathbf{x}_f = 0 } } \tag{2.7.32}\]

这是用Hamiltonian表示的自由终点系统的一般边界条件。

2.7.2 Different Types of Systems

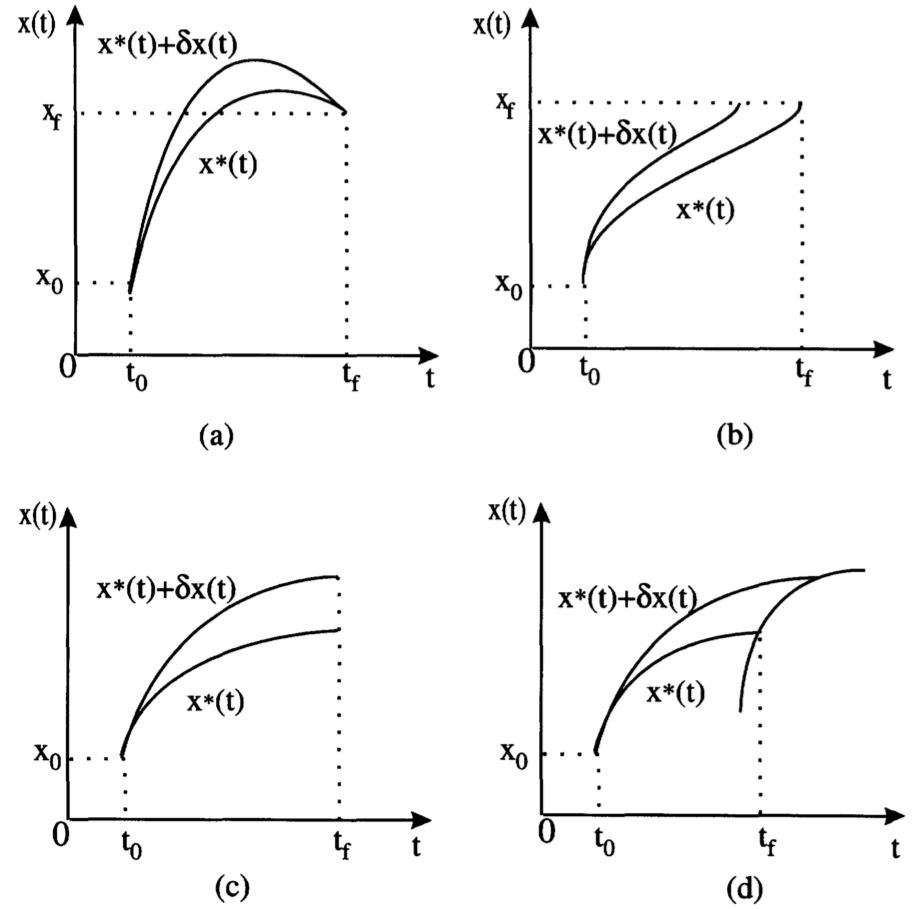
不同最终时间和最终状态情况下问题的陈述（如图2.9所示）。

• 1.Fixed-Final Time and Fixed-Final State System：由于\(t_f\)和\(\mathbf{x}(t_f)\)都是固定或指定的，所以\(\delta t_f\)和\(\delta \mathbf{x}(t_f)\)在一般边界条件(2.7.32)下都为零。
• 2.Free-Final Time and Fix ed-Final State System：由于\(t_f\)是自由的或未预先说明的，所以\(\delta t_f\)是任意的。由于\(\mathbf{x}(t_f)\)是固定或指定的，所以\(\delta \mathbf{x}(t_f)\)为零。那么，在一般边界条件(2.7.32)下任意\(\delta t_f\)的系数为零

\[\boxed{ \left( \mathcal{H}^* + \frac{\partial S}{\partial t} \right)_{* t_f} = 0 }\tag{2.7.33}\]

• 3.Fixed-Final Time and Free-Final State System：这里\(t_f\)是指定的，\(\mathbf{x}(t_f)\)是自由的，所以\(\delta t_f\)为零，\(\delta \mathbf{x}(t_f)\)是任意值，这意味着在一般边界条件(2.7.32)下任意\(\delta \mathbf{x}(t_f)\)的系数为零，即

\[\boxed{ \pmb{\lambda}^*(t_f) = \left( \frac{\partial S}{\partial \mathbf{x}} \right)_{* t_f} }\tag{2.7.34}\]

• 4.Free-Final Time and Dependent Free-Final State System：如果\(t_f\)和\(\mathbf{x}(t_f)\)相关，比如\(\mathbf{x}(t_f)\)落在如图2.8所示的移动曲线\(\pmb{\theta}\)上，那么

\[\mathbf{x}(t_f) = \pmb{\theta}(t_f) \quad \text{and} \quad \delta \mathbf{x}_f \approx \pmb{\dot{\theta}}(t_f) \delta t_f \tag{2.7.35}\]

根据式(2.7.35)，最优条件下的边界条件(2.7.32)变为

\[\left[ \left( \mathcal{H}+\frac{\partial S}{\partial t} \right)_* + \left( \frac{\partial S}{\partial \mathbf{x}} - \pmb{\lambda}^*(t) \right)_*^{\prime} \dot{\pmb{\theta}}(t) \right]_{t_f} \delta t_f = 0 \tag{2.7.36}\]

由于\(t_f\)自由，所以\(\delta t_f\)是任意的。因此，\(\delta t_f\)的系数为零，即

\[\left[ \left( \mathcal{H}+\frac{\partial S}{\partial t} \right)_* + \left( \frac{\partial S}{\partial \mathbf{x}} - \pmb{\lambda}^*(t) \right)_*^{\prime} \dot{\pmb{\theta}}(t) \right]_{t_f} = 0 \tag{2.7.37}\]

• 5.Free-Final Time and Independent Free-Final State：如果\(t_f\)和\(\mathbf{x}(t_f)\)无关，那么\(\delta t_f\)和\(\delta \mathbf{x}(t_f)\)也是无关的，最优条件下的边界条件为

\[\left( \mathcal{H} + \frac{\partial S}{\partial t} \right)_{* t_f} = 0 \tag{2.7.38}\] \[\left( \frac{\partial S}{\partial \mathbf{x}} - \pmb{\lambda}^*(t) \right)_{* t_f} = 0 \tag{2.7.39}\]

2.7.3 Sufficient Condition

  利用(2.7.14)(2.7.28)和(2.7.37)，得到

\[\begin{aligned} \delta^2 J & = \int_{t_0}^{t_f} \left[ \frac{\partial^2 \mathcal{H}}{\partial \mathbf{x}^2} (\delta \mathbf{x}(t))^2 + \frac{\partial^2 \mathcal{H}}{\partial \mathbf{u}^2} (\delta \mathbf{u}(t))^2 + 2 \frac{\partial^2 \mathcal{H}}{\partial \mathbf{u} \partial \mathbf{x}} (\delta \mathbf{u}(t) \delta \mathbf{x}(t)) \right]_* dt \\ & = \int_{t_0}^{t_f} \begin{bmatrix} \delta \mathbf{x}'(t) & \delta \mathbf{u}'(t) \end{bmatrix} \begin{bmatrix} \frac{\partial^2 \mathcal{H}}{\partial \mathbf{x}^2} & \frac{\partial^2 \mathcal{H}}{\partial \mathbf{u} \partial \mathbf{x}} \\[2ex] \frac{\partial^2 \mathcal{H}}{\partial \mathbf{u} \partial \mathbf{x}} & \frac{\partial^2 \mathcal{H}}{\partial \mathbf{u}^2} \end{bmatrix}_* \begin{bmatrix} \delta \mathbf{x}(t) \\ \delta \mathbf{u}(t) \end{bmatrix} dt \\ & = \int_{t_0}^{t_f} \begin{bmatrix} \delta \mathbf{x}'(t) & \delta \mathbf{u}'(t) \end{bmatrix} \Pi \begin{bmatrix} \delta \mathbf{x}(t) \\ \delta \mathbf{u}(t) \end{bmatrix} dt \end{aligned} \tag{2.7.40}\]

要求最小值，二阶变分\(\delta^2 J\)必须为正，即矩阵\(\Pi\)必须是正定的。但是，重要条件为\(\mathcal{H}\)关于\(\mathbf{u}(t)\)的二阶偏导数必须是正的，即

\[\boxed{ \left( \frac{\partial^2 \mathcal{H}}{\partial \mathbf{u}^2} \right)_* \gt 0 }\tag{2.7.42}\]

对于最大值，(2.7.42)的符号不变。

2.7.4 Summary of Pontryagin Procedure

  考虑自由-终时间和自由-终状态的Bolza问题，希望最小化性能指标

\[J = S(\mathbf{x}(t_f),t_f) + \int_{t_0}^{t_f} {V(\mathbf{x}(t),\mathbf{u}(t),t)}dt \tag{2.7.43}\]

被控对象的描述为

\[\mathbf{\dot{x}}(t) = \mathbf{f} ( \mathbf{x}(t),\mathbf{u}(t),t ) \tag{2.7.44}\]

边界条件为

\[\mathbf{x}(t_0) = \mathbf{x}_0; \qquad \mathbf{x}(t_f) \text{ is free and } t_f \text{ is free} \tag{2.7.45}\]

这里的\(\mathbf{u}(t)\)是不受限的。完整的流程（称为Pontryagin Principle）如表2.1所示。

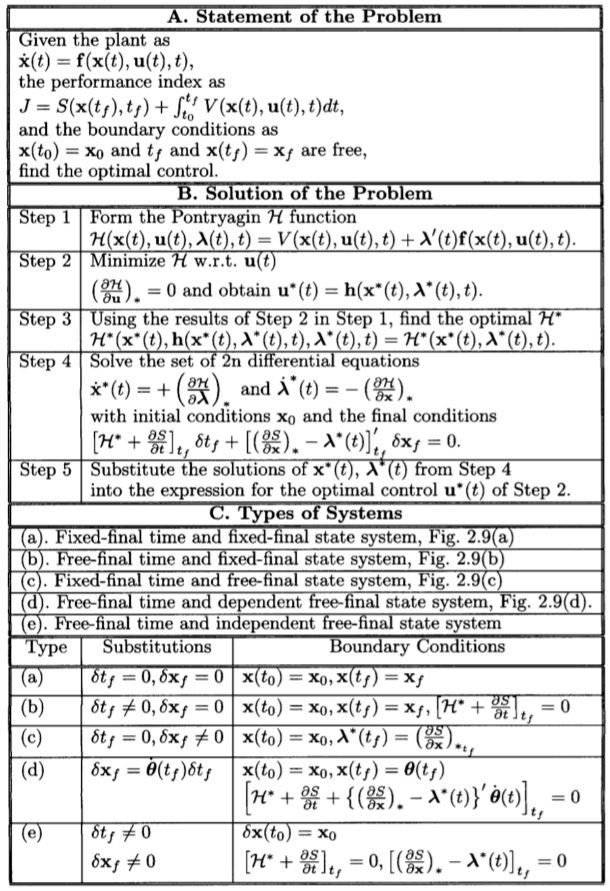
2.2.8 Summary of Variational Approach

2.8.1 Stage 1: Optimization of a Functional

  考虑如下函数的最优值：

\[J = \int_{t_0}^{t_f} {V(\mathbf{x}(t),\mathbf{\dot{x}}(t),t)} dt \tag{2.8.1}\]

边界条件为

\[\mathbf{x}(t_0) \text{ is fixed and } \mathbf{x}(t_f) \text{ is free} \tag{2.8.2}\]

那么，最优函数\(\mathbf{x}^*(t)\)应满足Euler-Lagrange方程

\[\boxed{ \left( \frac{\partial V}{\partial \mathbf{x}} \right)_* - \frac{d}{st} \left( \frac{\partial V}{\partial \mathbf{\dot{x}}} \right)_* = 0 }\tag{2.8.3}\]

自由终值点需要满足的一般边界条件为

\[\boxed{ \left[ V - \mathbf{\dot{x}}'(t) \left( \frac{\partial V}{\partial \mathbf{\dot{x}}} \right) \right]_{*t_f} \delta t_f + \left( \frac{\partial V}{\partial \mathbf{\dot{x}}} \right)'_{*t_f} \delta \mathbf{x}_f = 0 }\tag{2.8.4}\]

边界条件的描述由给定的\(t_f\)和\(\mathbf{x}(t_f)\)决定。

  最优值的充分条件为Legendre condition

\[\boxed{ \left( \frac{\partial^2 V}{\partial \mathbf{\dot{x}}^2} \right)_* \gt 0 } \text{ for minimum} \tag{2.8.5}\] \[\boxed{ \left( \frac{\partial^2 V}{\partial \mathbf{\dot{x}}^2} \right)_* \lt 0 } \text{ for maximum} \tag{2.8.6}\]

2.8.2 Stage 2: Optimization of a Functional with Condition

  考虑如下泛函的优化

\[J = \int_{t_0}^{t_f} {V(\mathbf{x}(t),\mathbf{\dot{x}}(t),t)} dt \tag{2.8.7}\]

边界条件为

\[\mathbf{x}(t_0) \text{ is fixed and } \mathbf{x}(t_f) \text{ is free} \tag{2.8.8}\]

约束条件为

\[\mathbf{g}(\mathbf{x}(t),\mathbf{\dot{x}}(t),t) = 0 \tag{2.8.9}\]

这里，条件(2.8.9)被融入进了增广泛函

\[J_a = \int_{t_0}^{t_f} { \mathcal{L} (\mathbf{x}(t),\mathbf{\dot{x}}(t),\pmb{\lambda}(t),t) } dt \tag{2.8.10}\]

其中，\(\pmb{\lambda}(t)\)为拉格朗日乘数（也称协态函数），\(\mathcal{L} (\mathbf{x}(t),\mathbf{\dot{x}}(t),\pmb{\lambda}(t),t)\)为Lagrangian

\[\boxed{ \mathcal{L} (\mathbf{x}(t),\mathbf{\dot{x}}(t),\pmb{\lambda}(t),t) = V(\mathbf{x}(t),\mathbf{\dot{x}}(t),t) + \pmb{\lambda}'(t) \mathbf{g}(\mathbf{x}(t),\mathbf{\dot{x}}(t),t) }\tag{2.8.11}\]

对(2.8.10)的增广泛函使用前面Stage 1的结果，把被积函数\(\mathcal{V}\)换成\(\mathcal{L}\)。对于最优情况，增广泛函的EL方程为

\[\boxed{ \left( \frac{\partial \mathcal{L}}{\partial \mathbf{x}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\mathbf{x}}} \right)_* = 0 }\quad \text{state equation} \tag{2.8.12}\] \[\boxed{ \left( \frac{\partial \mathcal{L}}{\partial \pmb{\lambda}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\pmb{\lambda}}} \right)_* = 0 }\quad \text{costate equation} \tag{2.8.13}\]

从(2.8.11)可知，\(\mathcal{L}\)与\(\dot{\pmb{\lambda}}^*(t)\)无关，因此协态\(\pmb{\lambda}(t)\)的EL方程即为约束条件(2.8.9)。自由终端需要满足的一般边界条件(2.8.4)（与\(\mathcal{L}\)相关）为

\[\boxed{ \left[ \mathcal{L} - \dot{\mathbf{x}}'(t) \left( \frac{\partial \mathcal{L}}{\partial \dot{\mathbf{x}}} \right) \right]_{* t_f} \delta t_f + \left( \frac{\partial \mathcal{L}}{\partial \dot{\mathbf{x}}} \right)'_{* t_f} \delta \mathbf{x}_f = 0 }\tag{2.8.14}\]

此边界条件会根据给定的\(t_f\)和\(\mathbf{x}(t_f)\)的性质改变。

2.8.3 Stage 3: Optimal Control System with Lagrangian Formalism

  这里，考虑标准控制系统，其被控对象描述如下

\[\dot{\mathbf{x}}(t) = \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t),t) \tag{2.8.15}\]

给定边界条件为

\[\mathbf{x}(t_0) \text{ is fixed and } \mathbf{x}(t_f) \text{ is free} \tag{2.8.16}\]

性能指标为

\[J(\mathbf{u}(t)) = \int_{t_0}^{t_f} {V(\mathbf{x}(t),\mathbf{u}(t),t)} dt \tag{2.8.17}\]

将被控对象方程(2.8.15)改写为条件的形式

\[\mathbf{g}(\mathbf{x}(t),\dot{\mathbf{x}}(t),\mathbf{u}(t),t) = \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t),t) - \dot{\mathbf{x}}(t) = 0 \tag{2.8.18}\]

构造增广泛函

\[J_a(\mathbf{u}(t)) = \int_{t_0}^{t_f} \mathcal{L}(\mathbf{x}(t),\dot{\mathbf{x}}(t),\mathbf{u}(t),\pmb{\lambda},t) dt \tag{2.8.19}\]

其中，Lagrangian为

\[\mathcal{L} = \mathcal{L}(\mathbf{x}(t),\dot{\mathbf{x}}(t),\mathbf{u}(t),\pmb{\lambda},t) = V(\mathbf{x}(t),\mathbf{u}(t),t) + \pmb{\lambda}'(t) { \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t),t) - \dot{\mathbf{x}}(t) } \tag{2.8.20}\]

利用之前Stage 2的结果。对于最优情况，增广泛函的EL方程为

\[\boxed{ \left( \frac{\partial \mathcal{L}}{\partial \mathbf{x}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\mathbf{x}}} \right)_* = 0 }\quad \text{state equation} \tag{2.8.21}\] \[\boxed{ \left( \frac{\partial \mathcal{L}}{\partial \pmb{\lambda}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\pmb{\lambda}}} \right)_* = 0 }\quad \text{costate equation} \tag{2.8.22}\] \[\boxed{ \left( \frac{\partial \mathcal{L}}{\partial \mathbf{u}} \right)_* - \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\mathbf{u}}} \right)_* = 0 }\quad \text{control equation} \tag{2.8.23}\]

由(2.8.20)可知，\(\mathcal{L}\)与\(\dot{\pmb{\lambda}}^*(t)\)和\(\dot{\mathbf{u}}^*(t)\)无关，(2.8.22)的EL方程和约束条件(2.8.28)一样。自由终端需要满足的一般边界条件(2.8.14)为

\[\boxed{ \left[ \mathcal{L} - \dot{\mathbf{x}}'(t) \left( \frac{\partial \mathcal{L}}{\partial \dot{\mathbf{x}}} \right) \right]_{* t_f} \delta t_f + \left( \frac{\partial \mathcal{L}}{\partial \dot{\mathbf{x}}} \right)'_{* t_f} \delta \mathbf{x}_f = 0 }\tag{2.8.24}\]

此边界条件会根据给定的\(t_f\)和\(\mathbf{x}(t_f)\)的性质改变。

2.8.4 Stage 4: Optimal Control System with Hamiltonian Formalism: Pontryagin Principle

  将之前的Lagrangian形式转化成Hamiltonian形式，通过定义Hamiltonian函数

\[\boxed{ \mathcal{H}(\mathbf{x}(t), \mathbf{u}(t), \pmb{\lambda}(t), t) = V(\mathbf{x}(t), \mathbf{u}(t), t) + \pmb{\lambda}^T(t) \mathbf{f}(\mathbf{x}(t), \mathbf{u}(t), t) }\tag{2.8.25}\]

这样(2.8.20)的Lagrangian就变为

\[\mathcal{L}(\mathbf{x}(t), \dot{\mathbf{x}}(t) \mathbf{u}(t), \pmb{\lambda}(t), t) = \mathcal{H}(\mathbf{x}(t), \mathbf{u}(t), \pmb{\lambda}(t), t) - \pmb{\lambda}^T(t) \dot{\mathbf{x}}(t) \tag{2.8.26}\]

利用上式，可以将EL方程改写成含Hamiltonian的形式

\[\boxed{ \dot{\mathbf{x}}^*(t) = + \left( \frac{\partial \mathcal{H}}{\partial \pmb{\lambda}} \right)_* }\text{ state equation} \tag{2.8.30}\] \[\boxed{ \dot{\pmb{\lambda}}^*(t) = - \left( \frac{\partial \mathcal{H}}{\partial \mathbf{x}} \right)_* }\text{ costate equation} \tag{2.8.31}\] \[\boxed{ 0 = + \left( \frac{\partial \mathcal{H}}{\partial \mathbf{u}} \right)_* }\text{ cotrol equation} \tag{2.8.32}\]

边界条件也可以改写成

\[\boxed{ \mathcal{H} | _{*t_f} \delta t_f - \pmb{\lambda}^{*T} (t_f) \delta \mathbf{x}_f = 0 }\tag{2.8.34}\]

充分条件为

\[\boxed{ \left( \frac{\partial^2 \mathcal{H}}{\partial \mathbf{u}^2} \right)_* \gt 0 }\text{ for minimum} \tag{2.8.35}\] \[\boxed{ \left( \frac{\partial^2 \mathcal{H}}{\partial \mathbf{u}^2} \right)_* \lt 0 }\text{ for maximum} \tag{2.8.36}\]

  状态、协态和控制方程可以根据给定的初始条件(2.8.16)和终止条件(2.8.34)求解，引出两点边值问题（TPBVP）。

Free-Final Point System with Final Cost Function

  此问题为Stage 4问题的延伸，增加了终点成本函数。被控对象描述和给定边界条件和Stage 3相同，性能指标为

\[J(\mathbf{u}(t)) = S(\mathbf{x}(t_f),t_f) + \int_{t_0}^{t_f} {V(\mathbf{x}(t),\mathbf{u}(t),t)} dt \tag{2.8.38}\]

通过把终点成本\(S\)写进积分项，可以改写性能指标(2.8.38)，然后利用Stage 3的结论来得到最优情况。因此，把性能指标改写成

\[J_1(\mathbf{u}(t)) = \int_{t_0}^{t_f} \bigg[ V(\mathbf{x}(t),\mathbf{u}(t),t) + \left( \frac{\partial S}{\partial \mathbf{x}} \right)' \dot{\mathbf{x}}(t) + \frac{\partial S}{\partial t} \bigg] dt \tag{2.8.40}\]

状态、协态和控制方程和Stage 4中相同，最终边界条件为

\[\boxed{ \left[ \mathcal{H} + \frac{\partial S}{\partial t} \right]_{*t_f} \delta t_f + \left[ \left( \frac{\partial S}{\partial \mathbf{x}} \right) - \pmb{\lambda}(t) \right]'_{*t_f} \delta \mathbf{x}_f = 0 }\tag{2.8.44}\]

充分条件与Stage 4相同。状态、协态和控制方程可以根据给定的初始条件和终止条件求解，即为两点边值问题（TPBVP）。

2.8.5 Salient Features

  1. 拉格朗日乘数的重要性：\(\pmb{\lambda}(t)\)也称协态（或伴随）函数。

(a) 引入拉格朗日乘数\(\pmb{\lambda}(t)\)来体现被控对象施加的约束关系。
(b) 协态变量\(\pmb{\lambda}(t)\)可以让我们对变量\(\mathbf{x}(t)\)和\(\mathbf{u}(t)\)分别用EL方程，而实际上这两个量根据被控对象方程是相关的。

  2. Lagrangian和Hamiltonian：在定义时用了矢量表示法，但是\(\pmb{\lambda}\)和\(\mathcal{H}\)都只是标量函数。

\[\begin{aligned} \mathcal{L} & = \mathcal{L} ( \mathbf{x}(t),\dot{\mathbf{x}}(t),\pmb{\lambda}(t),\mathbf{u}(t),t ) \\ & = V(\mathbf{x}(t),\mathbf{u}(t),t) + \pmb{\lambda}^T(t) \{ \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t),t) - \dot{\mathbf{x}}(t) \} \end{aligned} \tag{2.8.47}\] \[\begin{aligned} \mathcal{H} & = \mathcal{H} ( \mathbf{x}(t),\mathbf{u}(t),\pmb{\lambda}(t),t ) \\ & = V(\mathbf{x}(t),\mathbf{u}(t),t) + \pmb{\lambda}^T(t) \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t),t) \end{aligned} \tag{2.8.48}\]

  3. Hamiltonian的最优化

(a) 控制方程(2.8.32)表明Hamiltonian的最优值与控制量\(\mathbf{u}(t)\)有关。也就是说，初始性能指标(2.8.17)的最优等价于Hamiltonian关于\(\mathbf{u}(t)\)的最优。这样就可以把被控对象方程(2.8.15)条件下泛函的求解转化成一般的函数最值问题。

(b) 假设控制量是无约束或无边界的，并且可以取到控制条件\(\partial \mathcal{H} / \partial \mathbf{u} = 0\)。

(c) 如果\(\mathbf{u}(t)\)是受约束或有界的，如放大器饱和区、电机速度、或火箭推力等。受约束的最优控制系统将在第7章详细介绍。

(d) 不管\(\mathbf{u}(t)\)是否有约束，Pontryagin已经严密地证明了必须选择\(\mathbf{u}(t)\)来最小化Hamiltonian。这是Pontryagin对最优控制理论最重要的贡献，此方法被称为Pontryagin Principle。在控制受限的情况下，为求解

\[\boxed{ \min_{\mathbf{u}\in U} \mathcal{H}( \mathbf{x}^*(t),\pmb{\lambda}^*(t),\mathbf{u}(t),t ) = \mathcal{H}( \mathbf{x}^*(t),\pmb{\lambda}^*(t),\mathbf{u}^*(t),t ) }\tag{2.8.49}\]

或者等价为

\[\boxed{ \mathcal{H}( \mathbf{x}^*(t),\pmb{\lambda}^*(t),\mathbf{u}^*(t),t ) \le \mathcal{H}( \mathbf{x}^*(t),\pmb{\lambda}^*(t),\mathbf{u}(t),t ) }\tag{2.8.50}\]

  4. Pontryagin Maximum Principle：性能指标\(J\)的最小化等价于\(-J\)的最大化，Pontryagin Principle的进一步介绍在第6章。

  5. 最优条件下的Hamiltonian：

\[\begin{aligned} \mathcal{H}^* = & \mathcal{H}( \mathbf{x}^*(t),\mathbf{u}^*(t),\pmb{\lambda}^*(t),t ) \\ \frac{d \mathcal{H}^*}{dt} = & \left( \frac{\partial \mathcal{H}}{\partial \mathbf{x}} \right)_*^T \dot{\mathbf{x}}^*(t) + \left( \frac{\partial \mathcal{H}}{\partial \pmb{\lambda}} \right)_*^T \dot{\pmb{\lambda}}^*(t) + \left( \frac{\partial \mathcal{H}}{\partial \mathbf{u}} \right)_*^T \dot{\mathbf{u}}^*(t) + \left( \frac{\partial \mathcal{H}}{\partial t} \right)_* \end{aligned} \tag{2.8.52}\]

利用状态、协态和控制方程(2.8.30)到(2.8.32) ，可以得到

\[\left( \frac{d \mathcal{H}}{dt} \right)_* = \left( \frac{\partial \mathcal{H}}{\partial t} \right)_* \tag{2.8.53}\]

这意味着，沿着最优轨迹时，\(\mathcal{H}\)对时间\(t\)的全微分与偏微分相同。如果\(\mathcal{H}\)不明确依赖于\(t\)，则有

\[\boxed{ \left. \frac{d \mathcal{H}}{dt} \right|_* = 0 }\tag{2.8.54}\]

沿最优轨迹\(\mathcal{H}\)关于时间\(t\)为常数。

  6. Two-Point Boundary Value Problem (TPBVP)：动态系统的最优控制问题会引出TPBVP。

(a) 状态和协态方程(2.8.30)和(2.8.32)可通过初始和终止条件求解。一般来说，这些方程是非线性、时变的，可能需要采用数值求解的方法。
(b) 对于任意类型的边界条件而言，状态和协态方程都是一样的。
(c) 对于最优控制系统，得到状态和协态方程很容易，但是计算很麻烦，所以需要平衡系统的最优化和计算量。

  7. Open-Loop Optimal Control：在求解TPBVP的状态和协态方程，并代入控制方程中，可以得到如图2.15所示的开环最优控制。

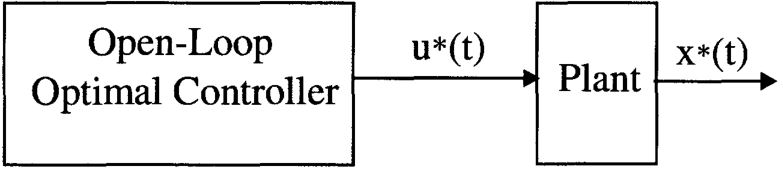
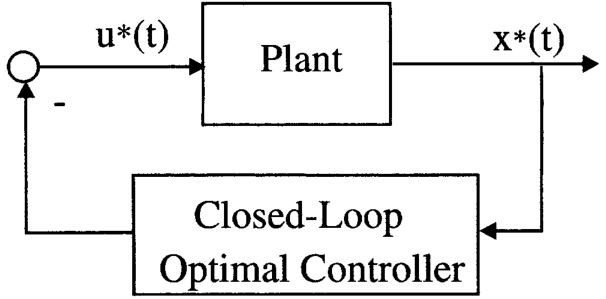
这其中需要构建一个开环最优控制器（OLOC），在大多数情况下很麻烦。并且，OLOC中并没有把被控对象的参数变化考虑在内。这促使我们从闭环最优控制（CLOC）的角度思考，i.e. 求解如图2.16所示的与状态\(\mathbf{x}^*(t)\)相关的最优控制\(\mathbf{u}^*(t)\)。CLOC具有对被控对象参数变化敏感、控制器结构简单等优点。闭环最优控制的内容在第7章。