Geometry of LP
2.1 Terminologies
Baseline Model: (LP)
\[\begin{aligned} \text{min} \quad & \mathbf{c}^T \mathbf{x} \\ \text{s.t.} \quad & \mathbf{Ax} = \mathbf{b} \\ & \mathbf{x} \ge 0 . \end{aligned}\]Feasible domain
\[P = \{ \mathbf{x} \in \mathbf{R}^n | \mathbf{Ax} = \mathbf{b} ,\ \mathbf{x} \ge 0 \}\]Feasible solution
\[\mathbf{x} \text{ is a } feasible \ solution \text{ if } \mathbf{x} \in P\]Consistency
\[\text{when } P \neq \emptyset ,\ \text{LP is } consistent\]Bounded feasible domain
\[P \text{ is } bounded \text{ if } \exists M \gt 0 \text{ such that } \|x\| \le M ,\ \mathbf{x} \in P\]在这种情况下,可以说"LP的可行域有界"。
Bounded LP
\[LP \text{ is } bounded \text{ if } \exists M \in R \text{ such that } \mathbf{c}^T \mathbf{x} \ge M ,\ \forall \mathbf{x} \in P\]问:LP的可行域有界 等价于 LP有界?
LP有界其可行域必有界,反之不成立。
Optimal solution
\[\mathbf{x}^* \text{ is an optimal solution if } \mathbf{x}^* \in P \text{ and } \mathbf{c}^T \mathbf{x}^* = \min_{x \in P} \mathbf{c}^T \mathbf{x}\]Optimal solution set
\[P^* = \{ \mathbf{x}^* | \mathbf{x}^* \text{ is optimal} \}\]We say \(\mathbf{x}^* \ solves\) LP, if \(\mathbf{x}^* \in P^*\).
2.2 Background knowledge
Observation 1: 标准形式的LP中的等式约束是解空间内的"hyperplane"。
Definition: hyperplane
对于一个向量\(\mathbf{a} \in \mathbf{R}^n ,\ \mathbf{a} \neq 0\)和一个标量\(\beta \in \mathbf{R}\),定义\(\color{green}{ H = \{ \mathbf{x} \in \mathbf{R}^n \lvert \mathbf{a}^T \mathbf{x} = \beta \} }\)为hyperplane(超平面)。
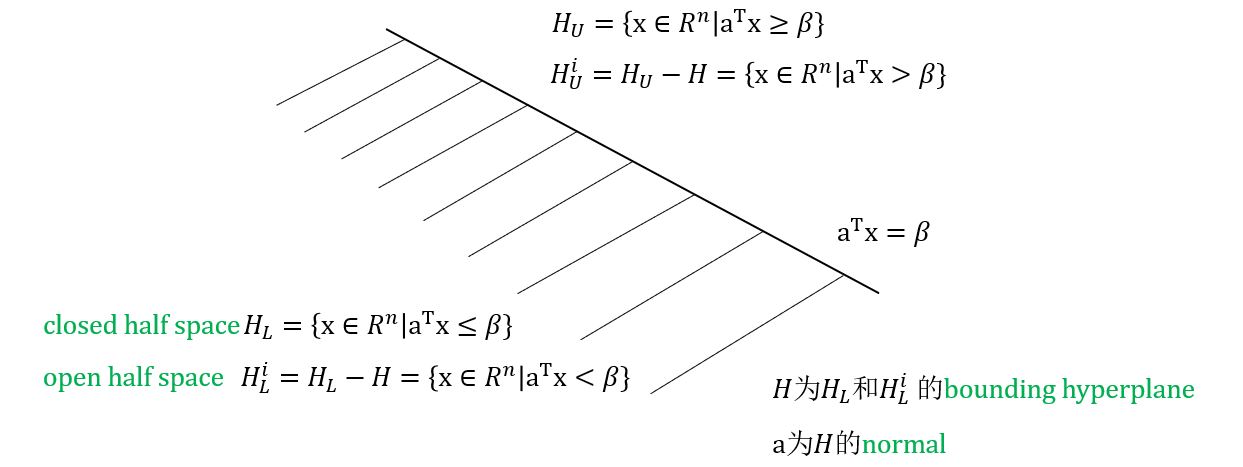
Property 1:法向量\(\mathbf{a}\)垂直于超平面\(H\)上的所有向量。
证: \(\forall \mathbf{y,z} \in H ,\ \mathbf{a}^T(\mathbf{y-z}) = \mathbf{a}^T \mathbf{y} - \mathbf{a}^T \mathbf{z} = \beta -\beta = 0\)
Property 2:法向量\(\mathbf{a}\)指向upper half space。
证: \(\forall \mathbf{z} \in H ,\ \mathbf{w} \in H_L^i ,\ \mathbf{a}^T(\mathbf{w-z}) = \mathbf{a}^T \mathbf{w} - \mathbf{a}^T \mathbf{z} \lt \beta -\beta = 0\)
Definition: polytope
一个polyhedral set或polyhedron是由有限个closed half spaces的交形成的。如果它是非空且有界的,则称它为polytope。
Property 3:标准的LP的可行域\(P = \{ \mathbf{x} \in \mathbf{R}^n \vert \mathbf{Ax=b} ,\ \mathbf{x} \ge 0 \}\)为多边集合。
Property 4:如果\(P \neq \emptyset\)且\(\exists \beta \in \mathbf{R}\),这样\(P \subset H_L := \{ \mathbf{x} \in \mathbf{R}^n \vert -\mathbf{c}^T \mathbf{x} \le \beta \}\)那么\(\min_{\mathbf{x} \in P} \mathbf{c}^T \mathbf{x} \ge \beta\)。进一步地,如果\(\mathbf{x}^* \in P \cap H\),那么\(\mathbf{x}^* \in P^*\)。
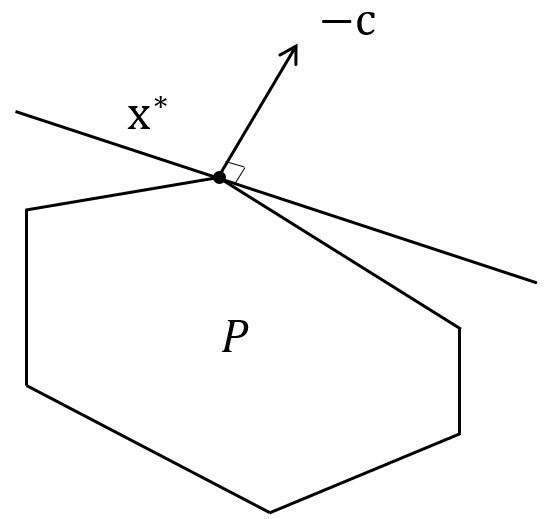
2.3 Graphic Method
- Step 1: 画出可行域\(P\)(如果\(P = \emptyset\),STOP!无解。)
- Step 2: 用\(\mathbf{-c}\)作为每个顶点的法向量来看对于某些\(\beta \in \mathbf{R}\),是否有\(P \in H_L := \{ \mathbf{x} \in \mathbf{R}^n \vert -\mathbf{c}^T \mathbf{x} \le \beta \}\)。
1.如果"YES",那么就找到了最优解。
2.如果"NO",那么此问题无下界。
Pros & Cons
优点:几何上简单
缺点:代数上复杂
—有多少个顶点?
—如何识别各个顶点?
例 给定以下LP
\[\begin{aligned} \text{min} \quad & -x_1 - 2x_2 \\ \text{s.t.} \quad & x_1 + x_2 \le 40 \\ & 2x_1 + x_2 \le 60 \\ & x_1 ,\ x_2 \ge 0 \\ \end{aligned}\]化成标准型,\(\mathbf{c} = \begin{bmatrix}-1 & -2 & 0 & 0\end{bmatrix}^T\),\(\mathbf{A} = \begin{bmatrix}1 & 1 & 1 & 0 \\ 2 & 1 & 0 & 1\end{bmatrix}\),\(\mathbf{b} = \begin{bmatrix}40 \\ 60\end{bmatrix}\)
\[\begin{aligned} \text{min} \quad & -x_1 - 2x_2 \\ \text{s.t.} \quad & x_1 + x_2 + x_3 = 40 \\ & 2x_1 + x_2 + x_4 = 60 \\ & x_1 ,\ x_2 ,\ x_3 ,\ x_4 \ge 0 \\ \end{aligned}\]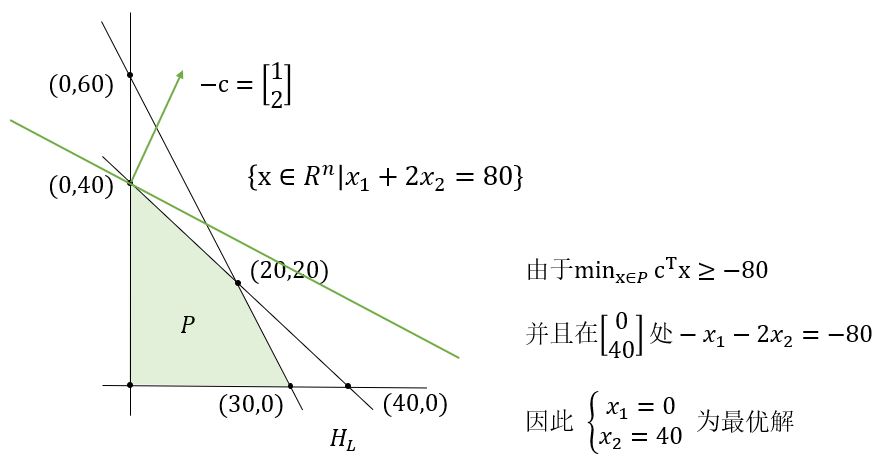
Any better way?
Simplex Method: 一种generate and manage可行解集(polyhedral set)的顶点的方法。
2.4 Fundamental theorem of LP
2.4.1 Background knowledge
Definition: linear, affine, conic, convex combination
\(\mathbf{x}^1, \mathbf{x}^2, \ldots, \mathbf{x}^P \ \in \mathbf{R}^n ,\ \lambda_1, \lambda_2, \ldots, \lambda_P \ \in \mathbf{R}\)且\(\mathbf{x} = \sum_{i=1}^P \lambda_i \mathbf{x}^i\),定义\(\mathbf{x}\)为\(\{ \mathbf{x}^1, \mathbf{x}^2, \ldots, \mathbf{x}^P \}\)的一个linear combination。
如果\(\sum_{i=1}^P \lambda_i = 1\),那么\(\mathbf{x}\)为\(\{ \mathbf{x}^1, \mathbf{x}^2, \ldots, \mathbf{x}^P \}\)的一个affine combination(仿射组合)。
如果\(\lambda_i \ge 0\),那么\(\mathbf{x}\)为\(\{ \mathbf{x}^1, \mathbf{x}^2, \ldots, \mathbf{x}^P \}\)的一个conic combination(圆锥组合)。
如果\(\sum_{i=1}^P \lambda_i = 1 ,\ \lambda_i \ge 0\),那么\(\mathbf{x}\)为\(\{ \mathbf{x}^1, \mathbf{x}^2, \ldots, \mathbf{x}^P \}\)的一个convex combination(凸组合)。
Definition: affine set, convex set and cone
令\(S\)为\(\mathbf{R}^n\)的一个子集
如果\(S\)中任意两点的仿射组合落在\(S\)内,那么\(S\)就是一个affine set。
如果\(S\)中任意两点的凸组合落在\(S\)内,那么\(S\)就是一个convex set。
如果对于所有的\(\mathbf{x} \in S\)且\(\lambda \ge 0\)都有\(\lambda \mathbf{x} \in S\),那么\(S\)就是一个cone(锥)。
例 Hyperplane是convex的,不是affine的。
证:\(\mathbf{x}^1 , \mathbf{x}^2\)是\(H\)内任意两点,要证\(H\)是凸集,即证凸组合\(\lambda_1 \mathbf{x}^1 + \lambda_2 \mathbf{x}^2 \in H ,\ \lambda_1 + \lambda_2 = 1 ,\ \lambda_1 , \lambda_2 \ge 0\)
\[\begin{aligned} \alpha^T (\lambda_1 \mathbf{x}^1 + \lambda_2 \mathbf{x}^2) = & \lambda_1 \alpha^T \mathbf{x}^1 + \lambda_2 \alpha^T \mathbf{x}^2 \\ = & \beta (\lambda_1 + \lambda_2) \\ = & \beta \end{aligned}\]例 Lower half space是convex的,不是affine的。
证:\(\mathbf{x}^1 , \mathbf{x}^2\)是\(H_L\)内任意两点,要证\(H_L\)是凸集,即证凸组合\(\lambda_1 \mathbf{x}^1 + \lambda_2 \mathbf{x}^2 \in H_L ,\ \lambda_1 + \lambda_2 = 1 ,\ \lambda_1 , \lambda_2 \ge 0\)
\[\begin{aligned} \alpha^T (\lambda_1 \mathbf{x}^1 + \lambda_2 \mathbf{x}^2) = & \lambda_1 \alpha^T \mathbf{x}^1 + \lambda_2 \alpha^T \mathbf{x}^2 \\ \le & \beta (\lambda_1 + \lambda_2) \\ = & \beta \end{aligned}\]要证\(H_L\)不是仿射的,可取\(\lambda_1 , \lambda_2 \le 0\),则有\(\alpha^T (\lambda_1 \mathbf{x}^1 + \lambda_2 \mathbf{x}^2) \ge \beta\),不在\(H_L\)内。
例 可行域 \(P = \{ \mathbf{x} \in \mathbf{R}^n \vert \mathbf{Ax} = \mathbf{b} ,\ \mathbf{x} \ge 0 \}\) 的几何意义?
1.\(P\)是一个polyhedral set。
2.\(P\)是一个convex set。
3.\(P\)是m个hyperplane与第一象限的cone的交集。
4.\(\mathbf{Ax} = \mathbf{b} ,\ \mathbf{x} \ge 0\)表明rhs向量\(\mathbf{b}\)落在由约束矩阵\(\mathbf{A}\)各列生成的cone内。 \(\mathbf{Ax} = [\mathbf{A}_1 \mathbf{A}_2 \cdots \mathbf{A}_n] \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \sum_{j=1}^n x_j \mathbf{A}_j \ \in \mathbf{R}^m\)
5.实际上,集合\(A_c = \{ \mathbf{y} \in \mathbf{R}^m \vert \mathbf{y=Ax} ,\ \mathbf{x} \in \mathbf{R}^n ,\ \mathbf{x} \ge 0 \}\)是由矩阵\(\mathbf{A}\)的各列生成的一个convex cone。
Definition: interior and boundary points
给定一个集合\(S \subset \mathbf{R}^n\),如果对于集合内一点\(\mathbf{x}\),\(\exists \epsilon \gt 0\)使得球\(B = \{ \mathbf{y} \in \mathbf{R}^n \vert \ \vert \vert \mathbf{x-y} \vert\vert \le \epsilon \} \ \subset S\),那么\(x\)就是集合\(S\)的一个interior point,否则就是boundary point。表示形式如下:
\[\begin{aligned} int(S) &= \{ \mathbf{x} \text{ is an interior point of S} \} \\ bdry(S) &= \{ \mathbf{x} \text{ is an boundary point of S} \} \end{aligned}\]问:凸集的边界点有何特别之处?
几何理解:过凸集的边界点可以找到supporting hyperplane把整个凸集划分到lower or upper half space中。
Separation Theorem
\(S \subset \mathbf{R}^n\)是一个凸集,那么对于任意的\(\mathbf{x} \in bdry(S)\),都存在一个hyperplane\(H\),使得\(\mathbf{x} \in H\)且\(S \subseteq H_L\)(或\(S \subseteq H_U\))
Question
—如何理解一个LP(二维或三维的)存在finite optimal solution,那么\(P\)的一个顶点即为最优?
Hint:考虑supporting hyperplane \(H = \{ \mathbf{x} \in \mathbf{R}^n \vert -\mathbf{c^T x} = \beta \}\)。
—更高维的情况是怎样的呢?
这将引出the Fundamental Theorem of LP。
问:所有的边界点都是一样的吗?
有些点坐在其它点的”肩”上(在其它点的连线上),有些不是。
Definition: extreme point
如果\(\mathbf{x}\)不可以由凸集\(S\)内其它点的凸组合表示,那么称\(\mathbf{x}\)是凸集\(S\)的一个extreme point。
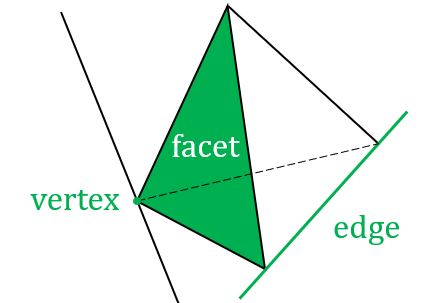
Definition: \(P\)是一个convex polyhedron,\(H\)为\(P\)的一个supporting hyperplane,那么将\(F = P \cap H\)定义为\(P\)的一个face,
当\(dim(F) = 0\)时,\(F\)为一个vector;
当\(dim(F) = 1\)时,\(F\)为一个edge;
当\(dim(F) = dim(P)-1\)时,\(F\)为一个facet。
Theorem: 如果\(P\)是一个convex polyhedron,\(\mathbf{x} \in P\),当且仅当\(\mathbf{x}\)是\(P\)的extreme point时,\(\mathbf{x}\)是\(P\)的vertex。
对于LP的可行域P而言,它的vertices即为extreme points。那么如何利用该性质来generate and manage所有的顶点呢?
当\(\mathbf{x}\)为\(P\)的一个极值点时,显然为\(\begin{cases} \mathbf{Ax=b} \\ \mathbf{x} \ge 0 \end{cases}\)的解。但是,极值点有何特别之处呢?
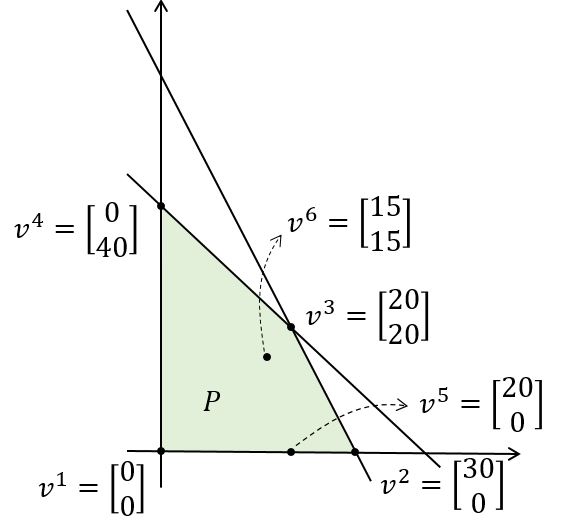
Verticies \(v^1 =\begin{bmatrix}0\\ 0\\ 40\\ 60\\ \end{bmatrix} ,\ v^2 =\begin{bmatrix}30\\ 0\\ 10\\ 0\\ \end{bmatrix} ,\ v^3 = \begin{bmatrix}20\\ 20\\ 0\\ 0\\ \end{bmatrix} ,\ v^4 =\begin{bmatrix}0\\ 40\\ 0\\ 20\\ \end{bmatrix}\)
Edge \(v^5 = \begin{bmatrix}20\\ 0\\ 20\\ 20\\ \end{bmatrix} \ \text{— one zero } x_i\) Interior \(v^6 = \begin{bmatrix}15\\15\\ 10\\ 15\\ \end{bmatrix} \ \text{— no zero } x_i\) \(n=4,\ m=2,\ n-m=2\)
\(\mathbf{Ax=b}\)中有\(m\)个线性方程,\(n\)个变量。
当\(n \gt m\)时,要求系统的线性方程只需要考虑\(m\)个线性方程中的\(m\)个变量。
求解极值点:令\(n-m\)个变量为零,并求出剩下的\(m\)个线性方程中的\(m\)个变量。
矩阵\(\mathbf{A}\)中与非零(正)变量相关的列最好是线性无关的。(将\(m\)个线性方程写成\(\mathbf{Mx=b}\),如果\(\mathbf{M}\)可逆,那么\(\mathbf{x} = \mathbf{M}^{-1} \mathbf{b}\)。)
例 Systems of equations
\[\begin{cases} & x_1 + x_2 + x_3 = 40 \\ & 2x_1 + x_2 + x_4 = 60 \\ & x_1 ,\ x_2 ,\ x_3 ,\ x_4 \ge 0 \\ \end{cases}\]Linear independence of columns如下,令任意两个\(x_i\)为零,即可得到一个extreme point。
\[\begin{bmatrix}1 \\ 2 \end{bmatrix} x_1 + \begin{bmatrix}1 \\ 1 \end{bmatrix} x_2 + \begin{bmatrix}1 \\ 0 \end{bmatrix} x_3 + \begin{bmatrix}0 \\ 1 \end{bmatrix} x_4 = \begin{bmatrix}40 \\ 60 \end{bmatrix}\]Theorem: 点\(\mathbf{x} \in P = \{ \mathbf{x} \in \mathbf{R}^n \vert \mathbf{Ax=b,x}\ge 0 \}\)为\(P\)的一个极值点,当且仅当\(\mathbf{A}\)中与正的\(\mathbf{x}\)相关的列是线性无关的。
证:为不失一般性,假设\(\mathbf{x}\)的前\(p\)个组成部分都是正的,其余的为零,i.e. \(\mathbf{x} = \begin{bmatrix} \overline{x} \\ 0 \end{bmatrix} \quad \text{where } \overline{x} = \begin{bmatrix} x_1 \\ \vdots \\ x_p \end{bmatrix}\) 并且将\(\mathbf{A}\)的前\(p\)列记为\(\overline{\mathbf{A}}\),那么\(\mathbf{Ax} = \overline{\mathbf{A}} \overline{\mathbf{x}} = \mathbf{b}\)。
假设\(\overline{\mathbf{A}}\)列不是线性无关的,那么\(\exists \overline{\mathbf{w}} = 0\)。注意当\(\epsilon\)足够小时,\(\overline{\mathbf{x}} \pm \epsilon \overline{\mathbf{w}} \ge 0\)并且\(\overline{\mathbf{A}}(\overline{\mathbf{x}} \pm \epsilon \overline{\mathbf{w}}) = \overline{\mathbf{A}} \overline{\mathbf{x}} = \mathbf{b}\)。
因此 \(\mathbf{y}^1 \begin{bmatrix} \overline{\mathbf{x}} + \epsilon \overline{\mathbf{w}} \\ 0 \end{bmatrix} \in P \qquad \mathbf{y}^2 \begin{bmatrix} \overline{\mathbf{x}} - \epsilon \overline{\mathbf{w}} \\ 0 \end{bmatrix} \in P\) 并且\(\mathbf{x} = \frac{1}{2} \mathbf{y}^1 + \frac{1}{2} \mathbf{y}^2\),所以\(\mathbf{x}\)不可能为\(P\)的一个顶点(极值点)。(tip:\(\mathbf{x}\)在两个点\(\mathbf{y}^1\)和\(\mathbf{y}^2\)之间,所以不可能是顶点。)
因此,\(\mathbf{x}\)是一个极值点 \(\Rightarrow\) \(\overline{\mathbf{A}}\)是线性无关的。
假设\(\mathbf{x}\)不是一个极值点,那么\(\mathbf{x} = \lambda \mathbf{y}^1 + (1-\lambda)\mathbf{y}^2\)对于有些\(\mathbf{y}^1,\mathbf{y}^2 \in P ,\ \mathbf{y}^1 \neq \mathbf{y}^2\)并且\(0 \lt \lambda \lt 1\)。
由于\(\mathbf{y}^1 \ge 0 ,\ \mathbf{y}^2 \ge 0\)并且\(0 \lt \lambda \lt 1\),\(\mathbf{y}^1\)剩下的\(n-p\)个元素必为零,i.e. \(\mathbf{y}^1 = \begin{bmatrix}\overline{\mathbf{y}}^1 \\ 0 \end{bmatrix}\)。
现在\(\mathbf{x-y}^1 = \begin{bmatrix} \overline{\mathbf{x}} - \overline{\mathbf{y}}^1 \end{bmatrix} \neq 0\)并且\(\mathbf{A} (\mathbf{x-y}^1) = \mathbf{Ax-Ay}^1 = \mathbf{b-b} =0\) \(\Rightarrow\) \(\overline{\mathbf{A}}\)的列是线性相关的。
因此\(\overline{\mathbf{A}}\)的列线性无关 \(\Rightarrow\) \(\mathbf{x}\)是一个极值点。
Managing extreme points algebraically
\(\mathbf{A}\)为\(m \times n\)的矩阵且\(m \le n\),如果\(\mathbf{A}\)有\(m\)个线性无关的列,那么则称\(\mathbf{A}\) full rank(full row rank)。
那么,
Definition: basic solution and basic feasible solution
如果令\(\mathbf{x}_N = 0\),并且求出\(\mathbf{Ax=Bx}_B = \mathbf{b}\)的解\(\mathbf{x}_B\),那么\(\mathbf{x}\)就是一个basic solution(bs)。
进一步地,如果\(\mathbf{x}_B \ge 0\),那么\(\mathbf{x}\)就是一个basic feasible solution(bfs)。
例
\[\begin{aligned} \text{min} \quad & -x_1 - 2x_2 \\ \text{s.t.} \quad & x_1 + x_2 + x_3 = 40 \\ & 2x_1 + x_2 + x_4 = 60 \\ & x_1 ,\ x_2 ,\ x_3 ,\ x_4 \ge 0 \\ \end{aligned}\] \[v^1 = \begin{bmatrix}0\\ 0\\ 40\\ 60\\ \end{bmatrix} ,\ v^2 = \begin{bmatrix}30\\ 0\\ 10\\ 0\\ \end{bmatrix} ,\ v^3 = \begin{bmatrix}20\\ 20\\ 0\\ 0\\ \end{bmatrix} ,\ v^4 = \begin{bmatrix}0\\ 40\\ 0\\ 20\\ \end{bmatrix} \quad \text{bfs}\] \[v^7 = \begin{bmatrix}40\\ 0\\ 0\\ -20\\ \end{bmatrix} ,\ v^8 = \begin{bmatrix}0\\ 60\\ -20\\ 0\\ \end{bmatrix} \quad \text{bs}\]Further results
Observation: 当\(\mathbf{A}\)不满秩时,那么
(1)\(\mathbf{Ax=b}\)无解,因此\(P = \emptyset\);或
(2)有些约束是冗余的。(此时去除冗余约束,得到的新的\(\mathbf{A}\)满秩。)
Corollary: \(P\)中一点\(\mathbf{x}\)为极值点,当且仅当\(\mathbf{x}\)是关于某个basis \(\mathbf{B}\)的bfs。
Corollary: Polyhedron \(P\)有有限个极值点。(\(\le C_n^m\))
What do extreme points bring us?
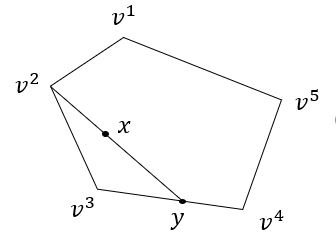
当可行域为非空polytope时,可行域内的任意一个点都可以用extreme points的凸组合表示。
Question: Can it be more general?
Extremal direction for unboudedness
当\(P\)是ubounded时,我们需要一个引导向无穷的方向。
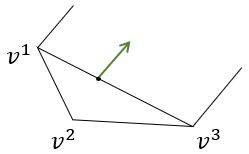
Definition: 向量\(\mathbf{d}(\neq 0) \in \mathbf{R}^n\)是\(P\)的一个extremal direction,如果对于所有的\(\{ \mathbf{x} \in \mathbf{R}^n \vert \mathbf{x=x}^0 + \lambda \mathbf{d} ,\ \lambda \ge 0 \}\)。
Observation:
(1)\(P\)是unbouded \(\Leftrightarrow\) \(P\)有extremal direction。
(2)\(\mathbf{d} (\neq 0)\)是\(P\)的一个extremal direction \(\Leftrightarrow\) \(\mathbf{Ad=0} \text{ and } \mathbf{d} \ge 0\)
2.4.2 Resolution theorem
Theorem: \(V = \{ v^i \in \mathbf{R}^n \vert i \in I \}\)为\(P\)的一系列extreme points,\(I\)为一个finite index set,那么\(\color{green}{\forall \mathbf{x} \in P}\),有\(\color{green}{\mathbf{x} = \sum_{i \in I}\lambda_i v^i + \mathbf{d}}\),其中\(\color{green}{\sum_{i \in I}\lambda_i = 1,\ \lambda_i \ge 0 \ \forall i \in I}\),\(\mathbf{d} = 0\)或为\(P\)的一个extremal direction。也可以写成\(\color{green}{ \mathbf{x} = \sum_{i \in I}\lambda_i v^i + s \mathbf{d} }\),对于有些\(\color{green}{s \ge 0}\)。
Implications of resolution theorem
Corollary: 如果\(P\)是bounded(a polytope),那么\(P\)中任意一个\(\mathbf{x}\)可以表示成它的extreme points的convex combination。
Corollary: 如果\(P\)是非空的,那么它至少有一个extreme point。
注意\(\mathbf{x} = \sum_{i \in I}\lambda_i v^i + s \mathbf{d}\)表明\(\mathbf{x}\)的objective value是由extreme points和extremal direction的目标函数值决定的。
2.4.3 Fundamental theorem
Theorem: 对于一个标准的LP,如果它的可行域\(P\)是非空的,那么the optimal objective value of \(\mathbf{z} = \mathbf{c}^T \mathbf{x} \text{ over } P\)要么是无下界的,要么在\(P\)的(至少)一个极值点处可以取到。
证:根据resolution theorem,存在以下两种情况:
Case 1: \(P\)有一个extremal direction \(\mathbf{d}\)使得\(\mathbf{c}^T \mathbf{d} \lt 0\),因此\(P\) unbouded且\(\mathbf{z} \rightarrow - \infty \text{ along } \mathbf{d}\)。
Case 2: \(P\)没有一个extremal direction \(\mathbf{d}\)使得\(\mathbf{c}^T \mathbf{d} \lt 0\),那么\(\forall \mathbf{x} \in P\),要么\(\mathbf{x} = \sum_{i \in I}\lambda_i v^i\)且\(\sum_{i \in I}\lambda_i = 1,\ \lambda_i \ge 0\),要么\(\mathbf{x} = \sum_{i \in I}\lambda_i v^i + \overline{\mathbf{d}}\)且\(\mathbf{c}^T \mathbf{x} \overline{\mathbf{d}} \ge 0\)。这两种情况下,
\[\begin{aligned} \mathbf{c}^T \mathbf{x} = & \mathbf{c}^T \big[\sum_{i \in I}\lambda_i v^i \big] (+ \mathbf{c}^T \mathbf{d} ) \\ \ge & \sum_{i \in I}\lambda_i (\mathbf{c}^T v^i) \\ \ge & \text{min}_{i \in I} (\mathbf{c}^T v^i) \sum_{i \in I}\lambda_i \\ = & \text{min}_{i \in I} (\mathbf{c}^T v^i) \\ = & \mathbf{c}^T v^{\text{min}} \end{aligned}\]因此在某个极值点处取到\(\mathbf{z}\)的最小值。
