决策树

1.1 基本决策树学习

Classical targeting problems

  • 非数值数据（nominal data）的分类问题
  • 离散
  • 没用相似的自然解释
  • 一般没有排序

Representation

  属性表而不是真值的向量。

Decision tree — concepts

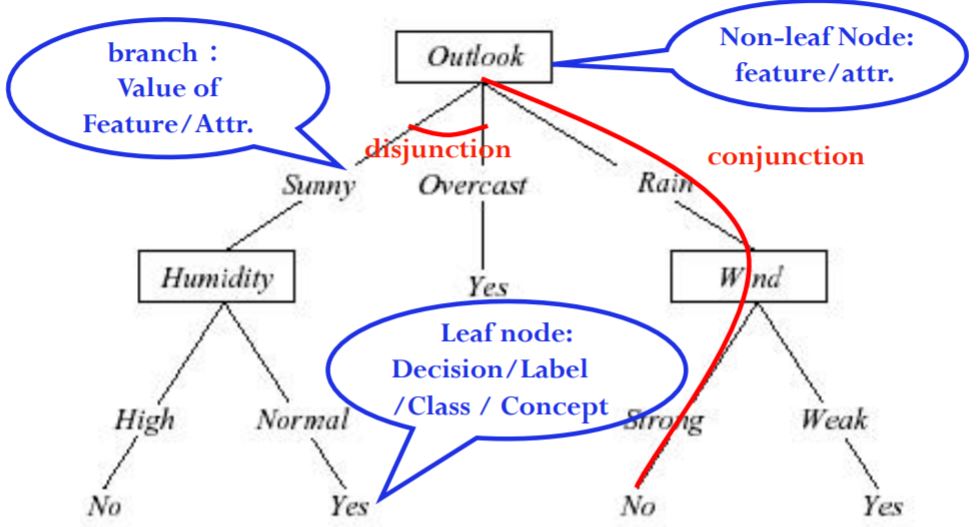
1.2 经典决策树算法

CART （分类与回归树）

一般框架：

  • 利用训练数据构造一棵决策树
  • 决策树将逐步将训练样本分解成越来越小的子集
  • 当每个子集都是纯的时停止
  • 或者当结果是可接受的时候

Classical DTreee Alg. – ID3

自顶向下，贪心搜索

递归算法

主循环：

  • A：下一步的最佳决策属性
  • 把A作为节点的决策属性
  • 对于\(A(vi)\)的每个值，创建新的节点后代
  • 将训练示例排序到叶节点
  • 如果训练样本完全分类，则RETURN，
    Else向下取到新的叶节点

Q1：哪个属性是最好的？

  Fundamental principle: simplicity
  在每个节点N上寻找一个属性查询T，使到达直系后代节点的数据尽可能"pure"。
  Purity - Impurity

提示

如何衡量不纯度？
— Entropy (熵) impurity is frequently used.

\[\color{green}{Entropy(N) = - \sum_j {P(w_j) \log_2 P(w_j)}}\]

定义\(0 \log 0 = 0\)。

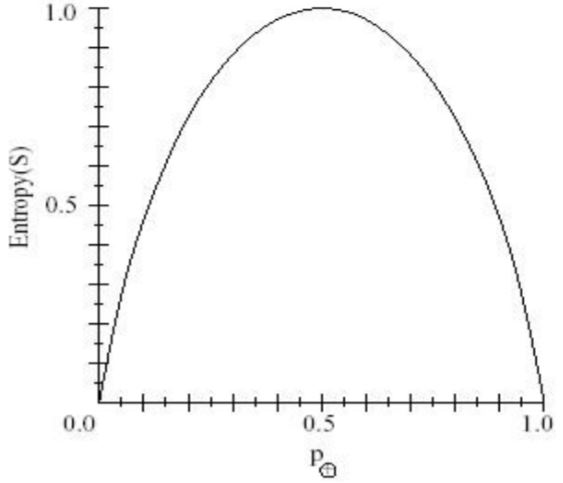
  在信息理论中，熵用来度量信息的纯/不纯，或者说是信息的不确定性。均匀分布的情况下，熵最大。

除熵外，其他计算方式
  Gini impurity \(i(N) = \sum_{i \neq j}{P(w_j)} P(w_j) = 1 - \sum_j P^2(w_j)\)
  Misclassification impurity \(i(N) = 1 - \max_j{P(w_i)}\)

度量熵的变化\(\color{green}{\Delta I(N)}\) — information gain (IG)

  期望熵随着对A的排序而下降。

\[Gain(S,A) \equiv Entropy(S) - \sum_{v \in Vlaues(A)} \frac{\vert S_v \vert}{S} Entropy(S_v)\]

Q2: 何时RETURN（停止分裂）?

  当训练样例被完美地分类了时。
Condition 1：如果当前子集内所有的数据都有相同的输出类，stop
Condition 2：如果当前子集内所有的数据都有相同的输入值，stop

补充

Possible Condition 3：如果所有的属性的IG值都是0，stop （A good idea?）

ID3所搜索的假设空间

（1）假设空间是完备的
  目标函数必定在其中

（2）输出单个假设
  （根据经验）不能超过20层

（3）无回溯
  局部极小

（4）每一步都用到了子集中所有数据
  基于统计的搜索选择
  对噪声数据具有鲁棒性

ID3的归纳偏置

注意：\(H\)是实例\(X\)的一个幂集。
  假设空间是没有限制的。

偏爱有高IG属性的树。
  试图找到最短的树。
  Bias是对某些假设的偏向（search bias），而不是假设空间的限制（language bias）。
  Occam's razor（奥卡姆剃刀原则）：偏向与数据吻合的最短假设。

1.3 Over-fitting

什么是过拟合？

  称\(\color{green}{h \in H}\)是过拟合的，如果存在另一个\(h' \in H\)使得\(\color{green}{err_{train}(h) \lt err_{train}(h')}\)且\(\color{green}{err_{train}(h) \gt err_{train}(h')}\)。

DTree中的过拟合

  每片叶子对应于一个单一的训练点，并且整个树只是一个查找表。

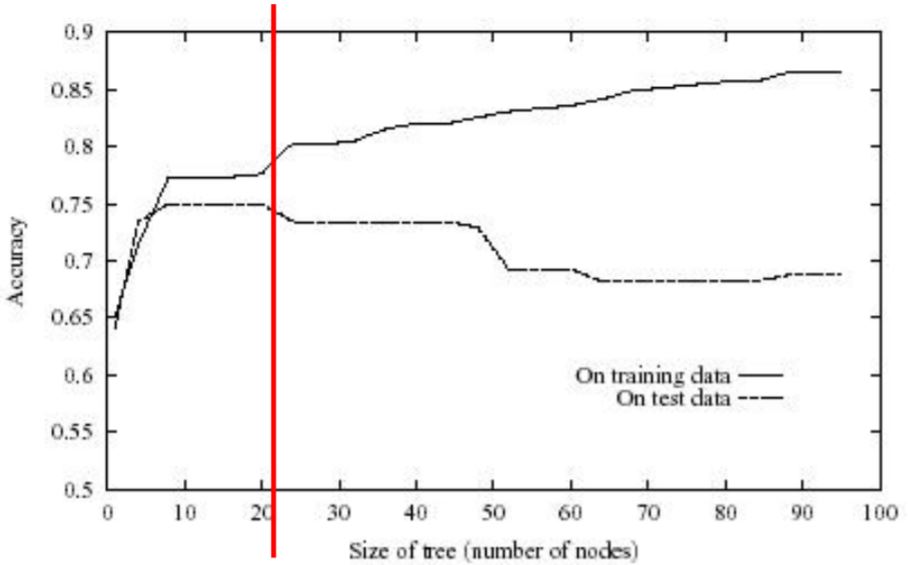
如何避免过拟合？

针对DTree的两种避免过拟合的方法：

  1. 当数据分割没有统计学意义时停止增长（预剪枝）
  2. 先长出完整的树，然后再剪枝（后剪枝）

1.4 Pruning

1.4.1 Pre-pruning

何时停止分裂？

  1. 实例数量
当到达一个节点的训练实例数小于训练集的一定百分比时，停止分裂。
忽略不纯和错误。

任何基于太少实例的决策都会导致方差，从而导致泛化错误。

  2. 信息增益值阈值
设置一个小的阈值，当\(\Delta i(s) \le q\)时停止分裂。
优点：利用了所有的训练数据，叶子节点可以位于树的不同层。
缺点：难以选择合适的阈值。

1.4.2 Post-pruning

如何选择最好的树？

  1. 通过训练数据来衡量性能（statistical pruning）
    置信度（confidence level）
  2. 在单独的验证数据集上衡量性能

MDL（Minimize Description Length，最小描述常数）：最小化树的大小和误分类树的大小

Reduced-error pruning

  • 将数据拆分为训练集和验证集
    验证集：已知标签，测试性能，在这个测试中模型不更新
  • 直到进一步修剪有害为止：
    评估修剪每个可能节点（加上它的根子树）对验证集的影响
    贪婪地删除最能提高验证集准确性的那个
补充

如何分配新叶子节点的标签？
— 分配最常见的类
— 给节点多类标签
每个类都有一个支持度（基于每个标签的训练数据的数量）。
在测试中：选择一个有概率的类，或者选择多个类。
— 如果是回归树（数字标签），可以取平均值或加权平均
— ……

Rule post-pruning

  1. 将树转换为等效的规则集
  2. 通过删除任何导致提高其估计准确性的先决条件来修剪每个规则
  3. 将规则排序为所需的顺序（按其估计的准确性）。
  4. 在对实例进行分类时，以相同的顺序使用最终规则。（规则被修剪后，可能无法再将它们重写为树。）

（常用的剪枝方法之一，e.g. C4.5）

补充

为什么剪枝前要把决策树转换成规则？
— 与上下文独立
否则，树在进行剪枝时只有两种选择：将节点整个移除或保留。
— 根节点与叶子节点之间没有区别
— 提高可读性

1.5 总结

决策树学习的特点：

  1. 基本思想来源于人的决策流程
  2. 简单，容易理解：如果……，就……
  3. 对噪声数据具有鲁棒性
  4. 广泛用于研究和实际应用
  5. 在采用更复杂的算法之前，通常会用决策树作为基准。

1.6 拓展

  1. 连续属性值
  2. 属性具有多个值
  3. 未知属性值
  4. 有成本的属性

更多信息

  奥卡姆剃刀原则，可以参考Domingos, The role of Occam's Razor in knowledge discovery. Journal of Data Mining and Knowledge Discovery, 3(4), 1999.

  决策森林：由C4.5构建的多个决策树

  C4.5 (C5.0): Data Mining Tools See5 and C5.0和Ross Quinlan的主页

归纳学习假设

  许多学习方法包含了从特定训练样例中获取一般概念的过程。
  归纳学习假设算法最多可以保证输出假设与训练数据的目标主题相符。
  注意：过拟合问题

  归纳学习假设：任一假设如果在足够大的训练样例集中很好地逼近目标函数，那么它也能在未见实例中很好地逼近目标函数。