Introduction of RL

1.1 Policy-based Approach

  (learning an actor)

1.1.1 Neural network as actor

• 神经网络输入：机器所观察到的内容，表示成一个向量或矩阵
• 神经网络输出：每个动作对应于输出层的一个神经元

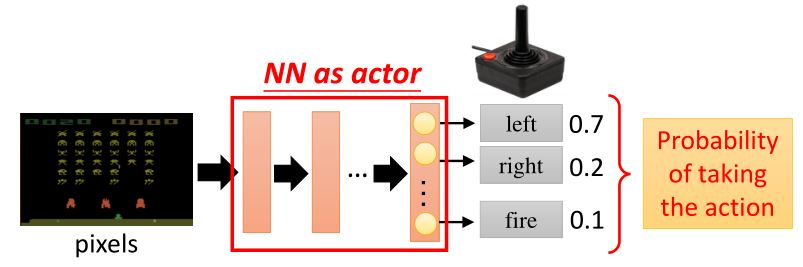
问：用神经网络代替查找表的好处？
Generalization

1.1.2 Goodness of actor

  给定一个网络参数为\(\theta\)的actor \(\pi_{\theta} (s)\)，用actor \(\pi_{\theta} (s)\)来玩游戏。我们的目标是最大化total reward：\(R_{\theta} = \sum_{t=1}^T r_t\)。哪怕是同一个actor，每次的\(R_{\theta}\)也是不同的。因为actor采用随机性策略，所以actor本身和游戏都是存在随机性的。

  定义\(\color{green}{\bar{R_{\theta}}}\)为\(\color{green}{R_{\theta}}\)的期望值。\(\bar{R_{\theta}}\)可以评估actor \(\pi_{\theta} (s)\)的好坏。

  一个episode可以被看作一个轨迹\(\tau\)，\(\tau = \{ s_1, a_1, r_1, s_2, a_2, r_2, \cdots, s_T, a_T, r_T \}\)，\(R_{\tau} = \sum_{n=1}^T r_n\)。如果用actor来玩游戏，每个\(\tau\)都有可能被采样到，其概率\(P(\tau \vert \theta)\)取绝于参数\(\theta\)。

\[\bar{R_{\theta}} = \sum_{\tau} R(\tau) P(\tau \vert \theta) \approx \frac{1}{N} \sum_{n=1}^N R(\tau^n)\]

  要求\(R_{\theta}\)的期望，需要对所以可能的轨迹求和。可以按策略\(\pi_{\theta}\)来玩\(N\)次游戏，得到\(\tau^1, \tau^2, \cdots, \tau^N\)，即从\(P(\tau \vert \theta)\)中进行\(N\)次采样。

1.1.3 Pick the best function

Gradient ascent

Policy gradient

  已知\(\bar{R_{\theta}} = \sum_{\tau} R(\tau) P(\tau \vert \theta)\)，其梯度为\(\nabla \bar{R_{\theta}} = \sum_{\tau} R(\tau) \nabla P(\tau \vert \theta)\)。因此\(R(\tau)\)无需是可微的，可以是一个黑箱（因为reward是由环境给出的）。

利用\(\frac{d \log(f(x))}{dx} = \frac{1}{f(x)} \frac{d f(x)}{dx}\)，可以进一步得到

\[\begin{aligned} \nabla \bar{R_{\theta}} = \sum_{\tau} R(\tau) P(\tau \vert \theta) \frac{\nabla P(\tau \vert \theta)}{P(\tau \vert \theta)} =& \sum_{\tau} R(\tau) P(\tau \vert \theta) \nabla \log P(\tau \vert \theta) \\ \approx& \frac{1}{N} \sum_{n=1}^N R(\tau^n) \nabla \log P(\tau^n \vert \theta) \end{aligned}\]

  轨迹\(\tau=\{ s_{1}, a_{1}, r_{1}, s_{2}, a_{2}, r_{2}, \cdots, s_{T}, a_{T}, r_{T} \}\)，所以

\[\begin{aligned} P(\tau \mid \theta) &= p\left(s_{1}\right) \prod_{t=1}^{T} p\left(a_{t} \mid s_{t}, \theta\right) p\left(r_{t}, s_{t+1} \mid s_{t}, a_{t}\right) \\ \log P(\tau \mid \theta) &= \log p\left(s_{1}\right) + \sum_{t=1}^{T} \log p\left(a_{t} \mid s_{t}, \theta\right)+\log p\left(r_{t}, s_{t+1} \mid s_{t}, a_{t}\right) \end{aligned}\] \[\boxed{ \nabla \log P(\tau \vert \theta) = \sum_{t=1}^{T} \log p\left(a_{t} \mid s_{t}, \theta\right) }\]

到这一步，我们已经略去了和\(\theta\)无关的项。

  梯度上升，\(\theta^{new} \leftarrow \theta^{old} + \eta \nabla \bar{R}_{\theta^{old}}\)

\[\begin{aligned} \nabla \bar{R_{\theta}} \approx \frac{1}{N} \sum_{n=1}^N R(\tau^n) \nabla \log P(\tau^n \vert \theta) =& \frac{1}{N} \sum_{n=1}^N R(\tau^n) \sum_{t=1}^{T_n} \nabla \log p(a_{t}^n \mid s_{t}^n, \theta) \\ =& \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} R(\tau^n) \nabla \log p(a_{t}^n \mid s_{t}^n, \theta) \end{aligned}\]

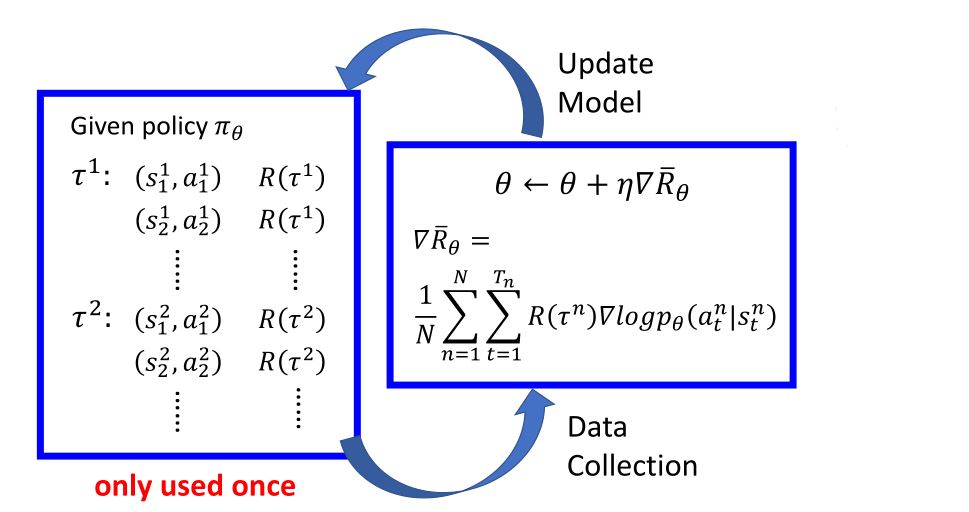
Add a baseline

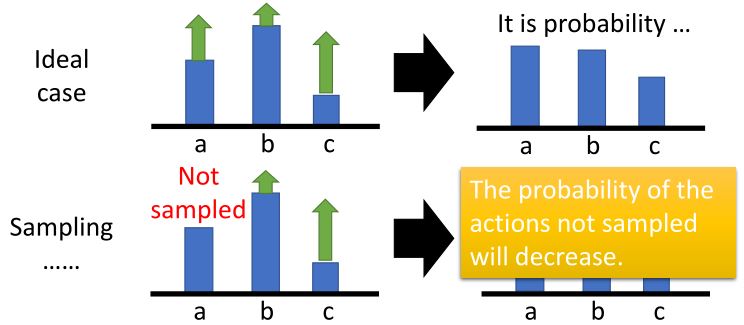
  在采样过程中，可能会漏掉某个动作，尽管它的奖励很高，但它的的概率会降低。可能存在\(R(\tau^n)\)一直为正的情况，需要减去一个bias。

\[\begin{aligned} &\theta^{new} \leftarrow \theta^{old} + \eta \nabla \bar{R}_{\theta^{old}} \\ &\nabla \bar{R_{\theta}} \approx \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} \big(R(\tau^n) - b\big) \nabla \log p(a_{t}^n \mid s_{t}^n, \theta) \end{aligned}\]

1.2 Value-based Approach

  (learning a critic)

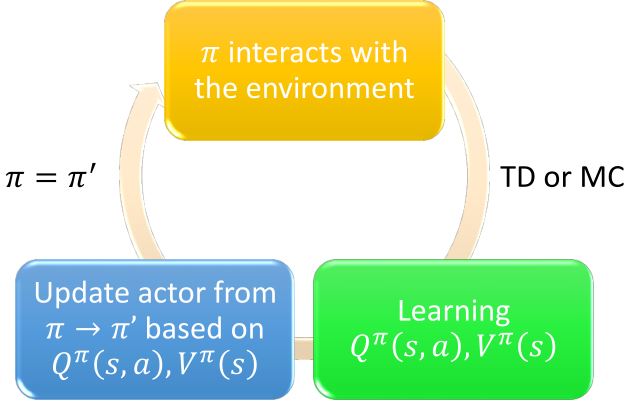
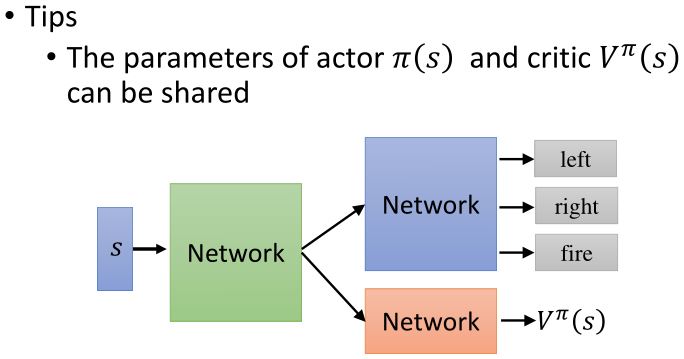
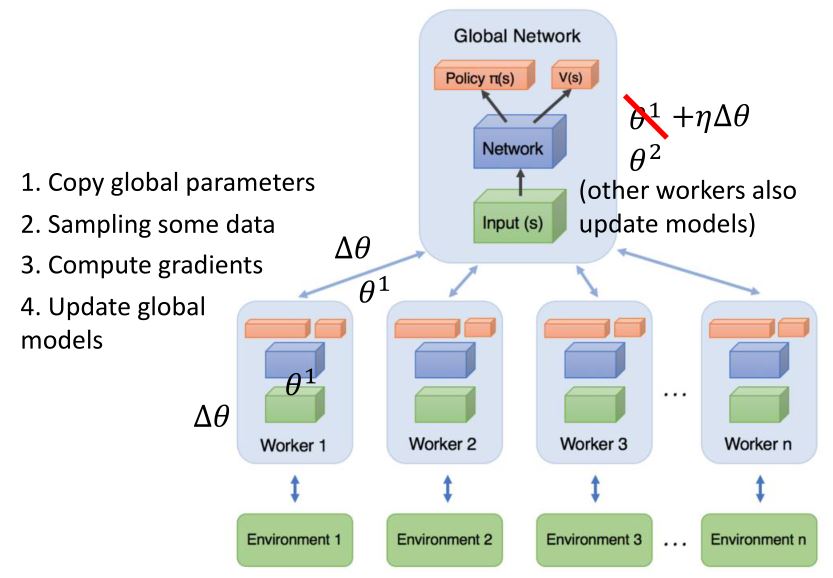
1.3 DRL: Actor-Critic